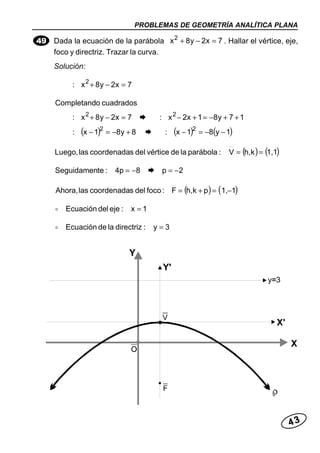
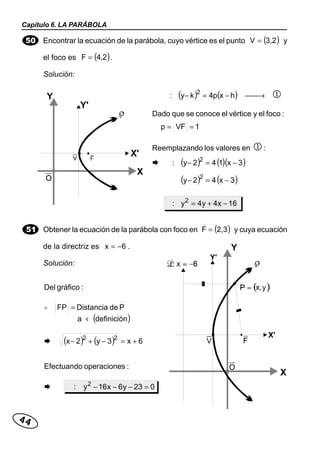
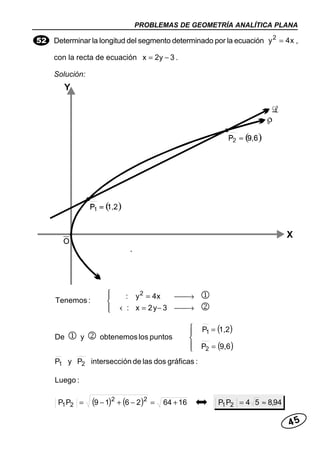
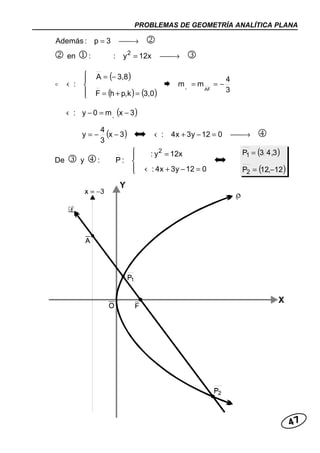
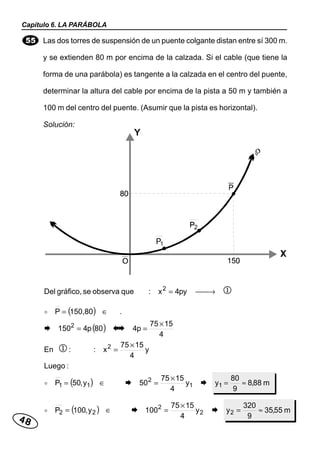
Este documento presenta varios problemas resueltos sobre geometría analítica plana relacionados con la parábola. Se calculan ecuaciones de parábolas dados diferentes elementos como vértice, foco y directriz. También se determinan puntos de intersección entre parábolas y rectas, y se calculan longitudes de segmentos.