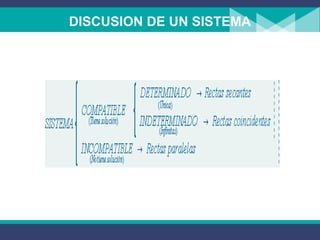
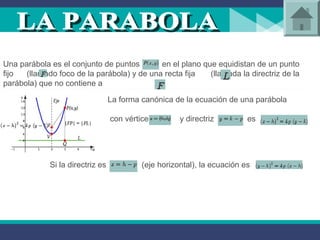
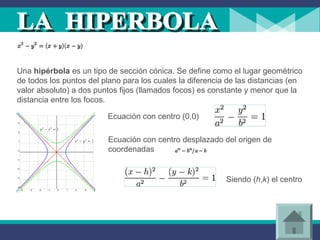
Este documento introduce la geometría analítica y describe algunas de sus aplicaciones principales. Explica cómo las ecuaciones algebraicas pueden representar líneas rectas, círculos, parábolas, elipses e hipérbolas. También cubre conceptos como coordenadas cartesianas, sistemas de ecuaciones y posiciones relativas entre rectas.

1. INTRODUCCION A LA GEOMETRIA
ANALITICA

2. LA RECTA
La ecuación de dichas rectas es
se representa con la función lineal de la forma
Rectas verticales
La ecuación de dichas rectas esRectas horizontales
Recta, en geometría, una línea infinita que describe de forma idealizada la
imagen real de un hilo tenso o de un rayo de luz.
Ecuaciones de la recta en el planoEcuaciones de la recta en el plano
Su expresión general es
donde m es la pendiente de la recta

3. INTRODUCCION A LA GEOMETRIA ANALITICAINTRODUCCION A LA GEOMETRIA ANALITICA
Geometría Analítica
tiene por objeto la
resolución de problemas
geométricos utilizando
métodos algebraicos.
El sistema que se
emplea para representar
gráficas fue ideado por
el filósofo y matemático
francés.

4. INTRODUCCION A LA GEOMETRIA ANALITICAINTRODUCCION A LA GEOMETRIA ANALITICA
Descartes (1596 - 1650),
quien usó su nombre
latinizado, Renatus
Cartesius, y por esta
razón se conoce con el
nombre de ejes
cartesianos

5. COORDENADAS EN EL PLANOCOORDENADAS EN EL PLANO
Un sistema de ejes cartesianos son dos
rectas perpendiculares que dividen al plano en
cuatro cuadrantes, y sirven para representar
cualquier punto del plano.
X
Y

6. INTERPRETACIÓN GEOMETRICA DE LASINTERPRETACIÓN GEOMETRICA DE LAS
COORDENADASCOORDENADAS
En Matemáticas, empleamos la notación OX
para designar al Eje X, y OY para el Eje Y.
Además, las expresiones d(A,OX) y d(A,OY)
indican las distancias del punto A a los ejes
cartesianos.

7. EJERCICIOS PARA RESOLVER EN CLASEEJERCICIOS PARA RESOLVER EN CLASE
1) Diseña una estrategia para
calcular la distancia entre A
y el origen de coordenadas,
es decir, d(A,O).
2) ¿Es cierto que d(H,O) =
d(A,O)?. ¿Es equilátero el
triángulo de vértices AOH?.
3) Calcula el perímetro y la
superficie del triángulo
AOH?.

8. RECTAS EN EL PLANORECTAS EN EL PLANO
En resumen:
 los puntos que cumplen y=1 representan una
recta horizontal.
 los puntos con x = 2, una recta vertical.
 los puntos con y = x, representan una recta
inclinada.

9. ECUACION DE PRIMER GRADO CON DOS INCOGNITASECUACION DE PRIMER GRADO CON DOS INCOGNITAS
Supongamos que
pretendemos obtener
todas las parejas de
números que sumen 2.
Evidentemente, existe
una infinidad de ellas,
pero todas están
relacionadas mediante
la ecuación x + y = 2.

10. INCIDENCIA DE PUNTO Y RECTAINCIDENCIA DE PUNTO Y RECTA
Se dice que un punto P es incidente con una
recta r cuando la recta pasa por el punto. En
este caso, el punto será una solución de la
ecuación.

11. POSICIONES RELATIVAS ENTRE DOS RECTAS
Analizar:
1)Determinar la posición relativa de las rectas -x
+ y = -1 , 2x + 3y + 3 = 0.
2)Determinar la posición relativa de las rectas x
+ 2y = 2 , 2x + 4y +1 = 0.
3)Determinar la posición relativa de las rectas -x
+ y = 1 , 2x - 2y = -2.

12. DISCUSION DE UN SISTEMA

13. Las rectas paralelas no tienen
ningún punto en común, por eso
los sistemas incompatibles no
tienen solución. Las rectas
secantes se cortan en un único
punto, la solución del sistema, que
se puede obtener gráficamente, en
caso de ser entera, o por
cualquiera de los métodos
algebraicos conocidos: sustitución,
igualación o reducción.

14. RESOLUCION DE UN SISTEMARESOLUCION DE UN SISTEMA
Al resolver un sistema indeterminado,
tendremos en cuenta que se corresponde con
rectas coincidentes, por lo tanto nos
quedaremos con la ecuación más simple.
Por ejemplo, en el sistema:

15. RESOLUCION DE UN SISTEMARESOLUCION DE UN SISTEMA
Nos quedamos con la primera ecuación,
x - y = 1 .
Despejamos una de las dos incógnitas, la
más fácil: x = y + 1.
La solución analítica del sistema se
expresa mediante las ecuaciones
paramétricas:
infinitas soluciones del sistema.

16. Se le conoce como geometría analítica al estudio de ciertos objetos
geométricos mediante técnicas básicas del análisis matemático y del
álgebra..

17. LA RECTA
La ecuación de dichas rectas es
se representa con la función lineal de la forma
Rectas verticales
La ecuación de dichas rectas esRectas horizontales
Recta, en geometría, una línea infinita que describe de forma idealizada la
imagen real de un hilo tenso o de un rayo de luz.
Ecuaciones de la recta en el planoEcuaciones de la recta en el plano
Su expresión general es
donde m es la pendiente de la recta

18. Circunferencia, en geometría, curva plana cerrada en la que cada uno de sus puntos
equidista de un punto fijo, llamado centro de la circunferencia.
.
LA ECUACION DE LA CIRCUNFERENCIA DE CENTRO (h,k) Y DE RADIO r ES
(x – h) 2 + (y-k) 2 = r 2

19. Una parábola es el conjunto de puntos en el plano que equidistan de un punto
fijo (llamado foco de la parábola) y de una recta fija (llamada la directriz de la
parábola) que no contiene a
La forma canónica de la ecuación de una parábola
con vértice y directriz es
Si la directriz es (eje horizontal), la ecuación es

20. La elipse es el lugar geométrico de los puntos del plano cuya suma de
distancias a dos puntos fijos es constante . Estos dos puntos fijos se llaman
focos de la elipse
Ecuación analítica de la elipse
(x – h ) 2 / a2 + ( y- k ) 2 / b 2 = 1
ECUACION DE LA ELIPSE DE
COORDENADAS DE CENTRO (h,k)
Yejes paralelos a los ejes coordenadas

21. Una hipérbola es un tipo de sección cónica. Se define como el lugar geométrico
de todos los puntos del plano para los cuales la diferencia de las distancias (en
valor absoluto) a dos puntos fijos (llamados focos) es constante y menor que la
distancia entre los focos.
Ecuación con centro (0,0)
Ecuación con centro desplazado del origen de
coordenadas
Siendo (h,k) el centro