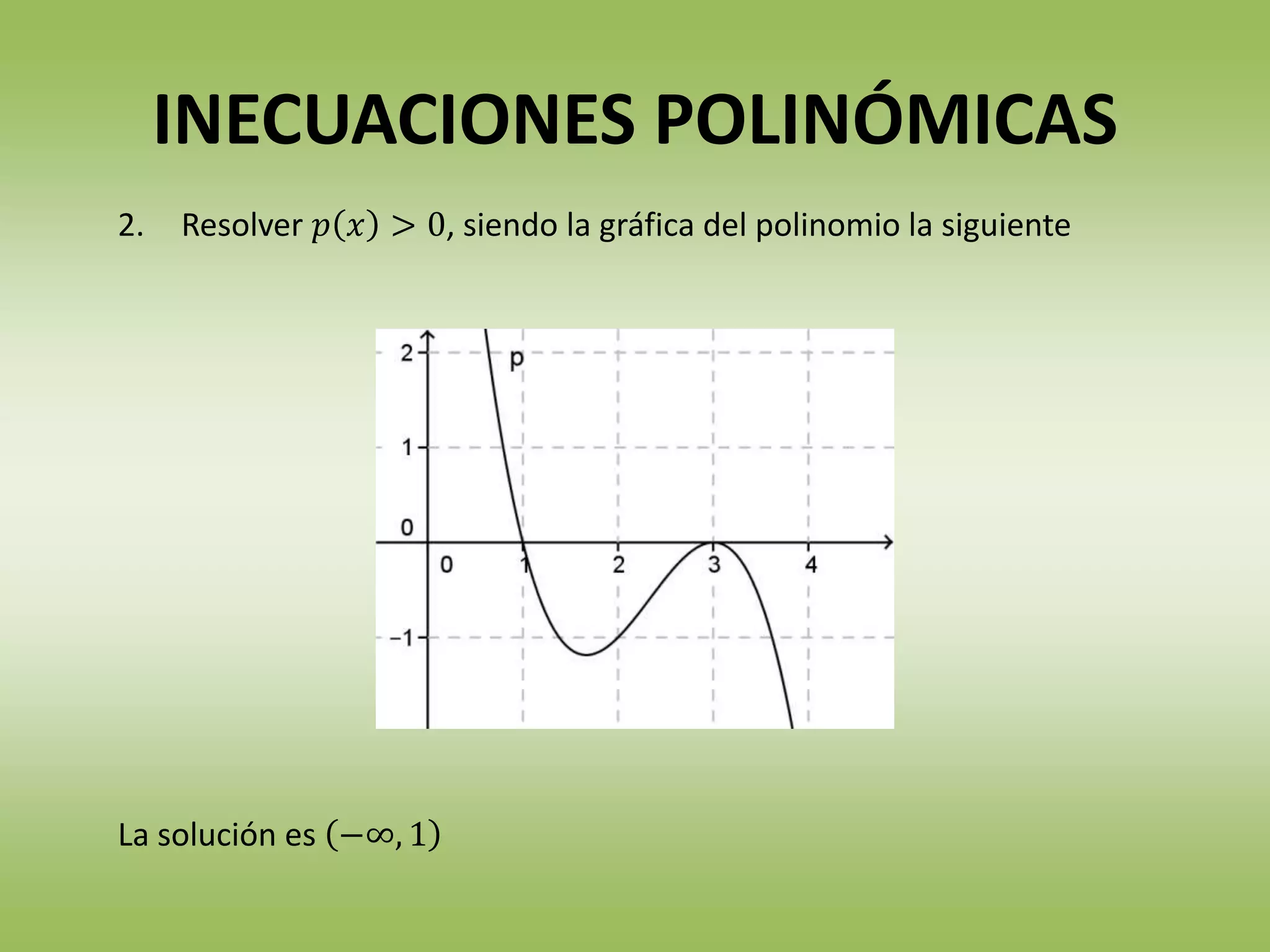
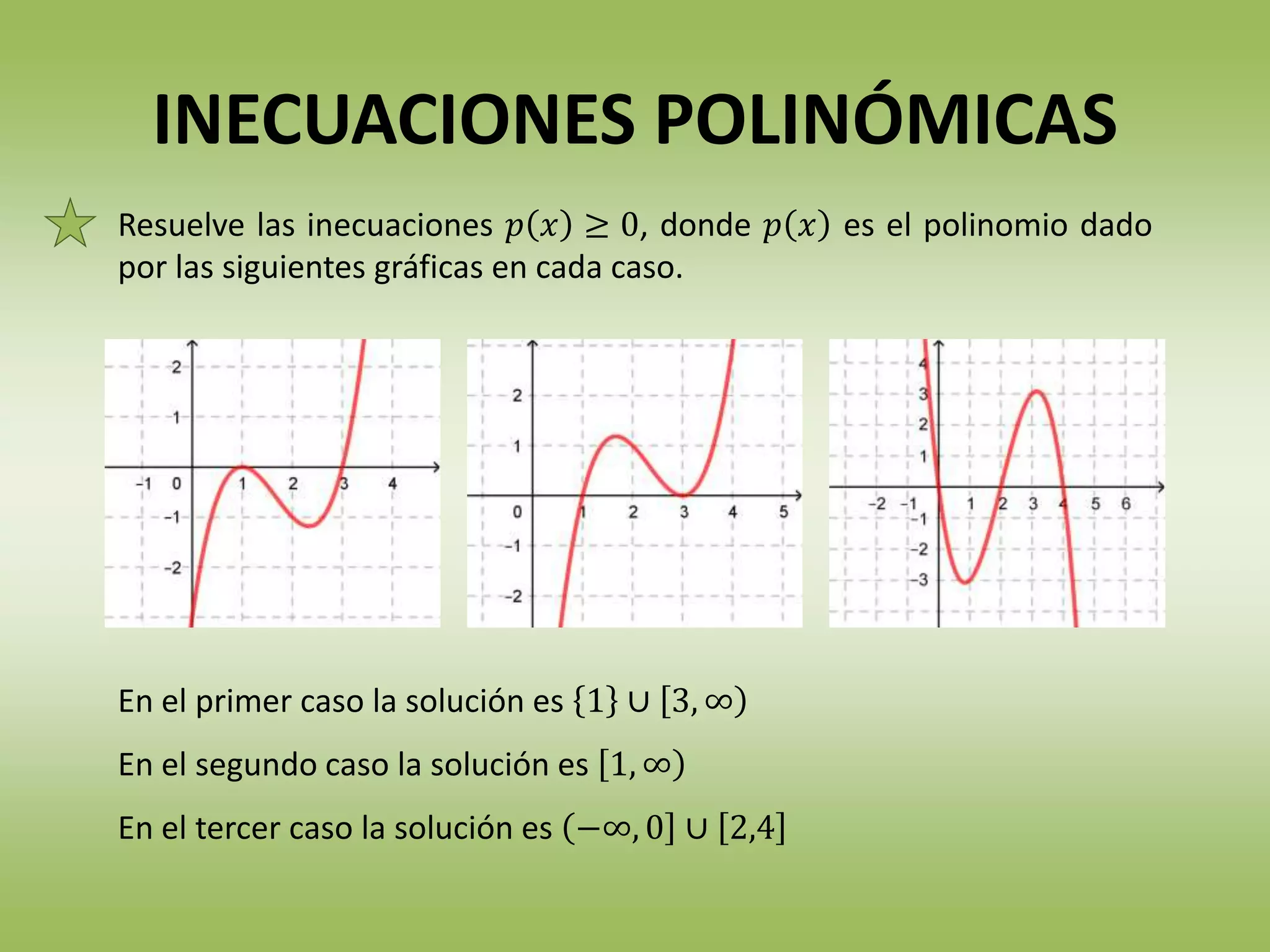
Este documento trata sobre inecuaciones y sistemas de inecuaciones. Define inecuaciones como desigualdades entre expresiones algebraicas y explica las reglas de equivalencia para mantener o cambiar el sentido de la desigualdad. Luego, cubre cómo resolver inecuaciones lineales, polinómicas y racionales de una incógnita, así como sistemas de inecuaciones.

1. Prof. Carlos A. Blanco
Inecuaciones y
sistemas de
inecuaciones

2. • Definiciones básicas. Desigualdades
• Reglas de equivalencia de las desigualdades
• Inecuaciones lineales de una incógnita
• Inecuaciones polinómicas
• Inecuaciones racionales
• Inecuaciones lineales de dos incógnitas
• Sistemas de inecuaciones
ÍNDICE

3. Una inecuación es una desigualdad entre dos expresiones algebraicas.
Hay que notar que siendo desigualdades, debemos conocer las
desigualdades que hay:
• < es “menor que” y lo entendemos como una desigualdad estricta:
Se tiene que 2 < 5 pero por el contrario 2 ≮ 2
• ≤ es “menor o igual que” y aquí si damos la posibilidad de que
ambos miembros sean iguales: 2 ≤ 5 así como 2 ≤ 2
• > es “mayor que” y, al igual que antes, lo entendemos como una
desigualdad estricta: Se tiene que 5 > 2 pero por el contrario 5 ≯ 5
• ≥ es “mayor o igual que” y, como antes, también damos la
posibilidad de que ambos miembros sean iguales: 5 ≥ 2 así como
5 ≥ 5
Las soluciones de una inecuación, por lo general, serán conjuntos de
puntos que cumplan las desigualdades. Normalmente se podrán
expresar en términos de intervalos.
DEFINICIONES BÁSICAS

4. Son conocidas como reglas de monotonía y son similares a las reglas de
la suma y del producto para las ecuaciones:
• Si se tiene una desigualdad
𝑎 ≤ 𝑏
Y se tiene una expresión c cualquiera, entonces se tiene que:
𝑎 + 𝑐 ≤ 𝑏 + 𝑐
• Si se tiene una desigualdad
𝑎 ≤ 𝑏
Y se tiene un número real 𝑐 > 0 cualquiera, entonces se tiene que:
𝑎 · 𝑐 ≤ 𝑏 · 𝑐
• Si por último se tiene una desigualdad
𝑎 ≤ 𝑏
Y se tiene un número real 𝑐 < 0 cualquiera, entonces se tiene que:
𝑎 · 𝑐 ≥ 𝑏 · 𝑐
REGLAS DE EQUIVALENCIA

5. −2𝑥 ≤ 6 ⇔ 𝑥 ≥
6
−2
⇔ 𝑥 ≥ −32𝑥 ≤ 6 ⇔ 𝑥 ≤
6
2
⇔ 𝑥 ≤ 3
Como consecuencia, a la hora de despejar:
• Si la incógnita está multiplicada por un número positivo, podemos despejar
como habitualmente manteniendo la desigualdad
• Si la incógnita está multiplicada por un número negativo, al despejar
deberemos cambiar la desigualdad de sentido:
2 ≤ 5 ⇔ 2 · −3 ≥ 5 · −32 ≤ 5 ⇔ 2 · 3 ≤ 5 · 32 ≤ 5 ⇔ 2 + 3 ≤ 5 + 3
Debemos entender que:
• Podremos sumar cualquier expresión o multiplicar por cualquier
número positivo a ambos miembros de una inecuación y la
desigualdad se mantiene.
• Por el contrario si multiplicamos por un número negativo ambos
miembros de una inecuación la desigualdad cambia de sentido.
Ejemplos:
REGLAS DE EQUIVALENCIA

6. Como siempre, debemos tener cuidado con los signos; especialmente en
los numeradores de las fracciones que tengan un signo menos delante.
Observa asimismo el cambio de sentido de la desigualdad al despejar: se ha
dividido entre un número negativo.
⇔ 3𝑥 − 12𝑥 + 4𝑥 ≥ 6 + 10 + 9 ⇔ −𝟓𝒙 ≥ 𝟐𝟓 ⇔ 𝒙 ≤ −𝟓
⇔ 3 𝑥 − 3 − 12𝑥 ≥ 6 − 2 2𝑥 − 5 ⇔ 3𝑥 − 9 − 12𝑥 ≥ 6 − 4𝑥 + 𝟏𝟎 ⇔
𝑥 − 3
2
− 2𝑥 ≥ 1 −
2𝑥 − 5
3
⇔ 6
𝑥 − 3
2
− 6 · 2𝑥 ≥ 6 · 1 − 6 ·
2𝑥 − 5
3
⇔
Es en éste último punto donde deberé tener cuidado con la desigualdad, si
se mantiene o si cambia de sentido.
Ejemplo
1. Quitar paréntesis 4. Trasponer términos
2. Quitar denominadores 5. Agrupar términos semejantes
3. Quitar paréntesis 6. Despejar
Para resolver inecuaciones lineales de una incógnita se seguirán los mismos
pasos que para las ecuaciones lineales:
INECUACIONES LINEALES
DE UNA INCÓNGITA

7. b) Eliminamos los denominadores, trasponemos y despejamos:
𝑥 − 3
2
−
2 𝑥 − 1
3
>
2
5
⇔ 30
𝑥 − 3
2
− 30
2𝑥 − 2
3
> 30
2
5
⇔
⇔ 15 𝑥 − 3 − 10 2𝑥 − 2 > 12 ⇔ 15𝑥 − 45 − 20𝑥 + 20 > 12 ⇔
⇔ 15𝑥 − 20𝑥 > 12 + 45 − 20 ⇔ −5𝑥 > 37 ⇔ 𝑥 < −
37
5
; −∞, −
37
5
a) Eliminamos los denominadores, trasponemos y despejamos:
𝑥 − 1
3
−
𝑥 − 2
2
≤
3
4
⇔ 12
𝑥 − 1
3
− 12
𝑥 − 2
2
≤ 12
3
4
⇔
⇔ 4 𝑥 − 1 − 6 𝑥 − 2 ≤ 9 ⇔ 4𝑥 − 4 − 6𝑥 + 12 ≤ 9 ⇔
⇔ 4𝑥 − 6𝑥 ≤ 9 + 4 − 12 ⇔ −2𝑥 ≤ 1 ⇔ 𝑥 ≥ −
1
2
; −
1
2
, ∞
a)
𝑥 − 1
3
−
𝑥 − 2
2
≤
3
4
b)
𝑥 − 3
2
−
2 𝑥 − 1
3
>
2
5
Resuelve las siguientes inecuaciones:
INECUACIONES LINEALES
DE UNA INCÓNGITA

8. La manera de resolver una inecuación polinómica es calcular el signo de
dicho polinomio, descomponiendo y evaluando el signo de sus factores.
Nota: Si la desigualdad fuera otra, sería lo mismo: 𝑝 𝑥 ≤ 0 nos
preguntarían los valores de 𝑥 para los que el polinomio es negativo o
nulo, y lo mismo con desigualdades estrictas.
Resolveremos inecuaciones polinómicas cuando estén en la forma
𝑝 𝑥 ≥ 0
Es decir, cuando todos los términos estén en un miembro de la
inecuación, quedando en el segundo miembro solamente un 0.
Observamos que en este caso lo que se está preguntando es para que
valores de 𝑥, el polinomio es positivo o nulo.
INECUACIONES POLINÓMICAS

9. −∞, 1 1 1,2 2 2, ∞
𝑥 − 2
𝑥 − 1
𝑥2 − 3𝑥 + 2 =
= 𝑥 − 2 𝑥 − 1
Si tenemos la inecuación:
𝑥2 − 3𝑥 + 2 ≥ 0
1. Descomponemos el polinomio calculando sus raíces (por Ruffini,
resolviendo la ecuación,…)
𝑥2
− 3𝑥 + 2 = 0 ⇔ 𝑥 =
3 ± 9 − 8
2
=
3 ± 1
2
=
2
1
⇒
⇒ 𝑥2 − 3𝑥 + 2 = 𝑥 − 2 𝑥 − 1
2. Elaboramos una tabla con los signos de sus factores de manera que
la línea superior es una recta real en la que colocamos los puntos
donde se hacen cero los factores que forman el polinomio.
INECUACIONES POLINÓMICAS

10. −∞, 1 1 1,2 2 2, ∞
𝑥 − 2
𝑥 − 1
𝑥2
− 3𝑥 + 2 =
= 𝑥 − 2 𝑥 − 1
++−
+−−
3. Evaluamos los factores del polinomio en cada uno de los intervalos:
• Tomamos un valor de 𝑥 en el intervalo −∞, 1 (por ejemplo
𝑥 = 0)
• Evaluamos el factor 𝑥 − 2 = 0 − 2 < 0, y de este modo
colocamos un signo – en la casilla correspondiente.
• Análogamente evaluamos el resto de los factores en los
intervalos. Se tiene entonces la tabla:
INECUACIONES POLINÓMICAS

11. Con lo que deducimos que la solución es el conjunto −∞,1 ∪ 2, ∞
Hay que notar que en este conjunto solución hemos incluido los
extremos de los intervalos puesto que son puntos donde la inecuación
se hace cero, y en este caso, soluciones también.
−∞, 1 1 1,2 2 2, ∞
𝑥 − 2 − + +
𝑥 − 1 − − +
𝑥2
− 3𝑥 + 2 =
= 𝑥 − 2 𝑥 − 1
+−+
5. Puesto que la inecuación era 𝑥2 − 3𝑥 + 2 ≥ 0, lo que preguntaban
eran los valores de 𝑥 para los que el polinomio era positivo:
4. Calculamos los signos del polinomio operando los signos de los
factores. Se tiene finalmente la tabla:
INECUACIONES POLINÓMICAS

12. Y la solución hubiera sido 1,2
−∞, 1 1 1,2 2 2, ∞
𝑥 − 2 − + +
𝑥 − 1 − − +
𝑥2 − 3𝑥 + 2 =
= 𝑥 − 2 𝑥 − 1
+ − +
Y la solución hubiera sido −∞, 1 ∪ 2, ∞
Del mismo modo, si hubiera sido 𝑥2 − 3𝑥 + 2 ≤ 0, entonces:
−∞, 1 1 1,2 2 2, ∞
𝑥 − 2 − + +
𝑥 − 1 − − +
𝑥2 − 3𝑥 + 2 =
= 𝑥 − 2 𝑥 − 1
+ − +
Si fuera 𝑥2 − 3𝑥 + 2 > 0, con los mismos pasos, hubiéramos obtenido:
INECUACIONES POLINÓMICAS

13. 
Y la solución hubiera sido 1,2
−∞, 1 1 1,2 2 2, ∞
𝑥 − 2 − + +
𝑥 − 1 − − +
𝑥2
− 3𝑥 + 2 =
= 𝑥 − 2 𝑥 − 1
+ − +
Y por último, si hubiera sido 𝑥2 − 3𝑥 + 2 < 0, la tabla hubiera sido:
INECUACIONES POLINÓMICAS

14. La inecuación 𝑥2 − 3𝑥 + 2 ≥ 0 busca los valores de 𝑥 para los que el
polinomio es positivo, es decir, para los que la función es positiva. Los
valores de 𝑥 para los que los valores de 𝑦 están por encima del eje 𝑥.
Los valores de 𝑥 para los que la gráfica está por encima del eje 𝑥.
x y
0 2
1 0
2 0
3 2
Interpretamos gráficamente estas inecuaciones.
Se tiene que la ecuación 𝑦 = 𝑥2 − 3𝑥 + 2 representa una función de
segundo grado, cuya gráfica es una parábola. Podemos dibujar la
parábola con una tabla de valores:
INECUACIONES POLINÓMICAS

15. Se tiene que la solución sería toda la recta real: ℝ
Observamos que se podrían dar los siguientes casos.
• Si se trata de una inecuación 𝑝 𝑥 ≥ 0, y el polinomio se representa
gráficamente:
INECUACIONES POLINÓMICAS

16. Entonces ningún punto sería solución. Es decir, la solución sería el
conjunto vacío ∅
• Si se tratara de una inecuación 𝑝 𝑥 ≤ 0, y el polinomio se
representa gráficamente:
INECUACIONES POLINÓMICAS

17. Para distinguirlo, evaluamos el polinomio en un punto cualquiera:
Si 𝑥 = 0 ⇒ 𝑥2 + 𝑥 + 2 = 02 + 0 + 2 = 2 > 0
Al ser positivo el valor de la parábola en 𝑥 = 0 concluimos que el dibujo
es el primero y así el polinomio es siempre positivo. La solución es ℝ
O bien su dibujo esO bien su dibujo es
Ejemplo: Resolver 𝑥2 + 𝑥 + 2 ≥ 0
Como antes, intentamos descomponer el polinomio
𝑥 =
−1 ± 1 − 8
2
=
−1 ± −7
2
⇒ 𝑥2
+ 𝑥 + 2 = 𝑥2
+ 𝑥 + 2
Al no tener raíces reales, el polinomio es irreducible. Gráficamente, la
parábola no corta al eje 𝑥, de modo que tenemos dos posibilidades:
INECUACIONES POLINÓMICAS

18. Nota: lo escribimos en forma de
conjunto, como en todos los
casos anteriores. Un conjunto
formado por un solo punto, o por
puntos aislados, lo denotamos
entre llaves.
Deducimos entonces que la solución es 3 , el punto 𝑥 = 3
Ejemplo: Resolver 𝑥2
− 6𝑥 + 9 ≤ 0
Descomponemos el polinomio
𝑥 =
6 ± 36 − 36
2
=
6 ± 0
2
= 3 doble ⇒ 𝑥2 − 6𝑥 + 9 = 𝑥 − 3 2
Al ser un factor elevado al cuadrado, deducimos que siempre va a tener
signo positivo, salvo donde se anule, que es en el punto 𝑥 = 3.
INECUACIONES POLINÓMICAS

19. La solución es −∞,1 ∪ 3
Resolvemos ahora unos ejercicios de inecuaciones dadas gráficamente:
1. Resolver 𝑝 𝑥 ≥ 0, siendo la gráfica del polinomio la siguiente
INECUACIONES POLINÓMICAS

20. La solución es −∞, 1
2. Resolver 𝑝 𝑥 > 0, siendo la gráfica del polinomio la siguiente
INECUACIONES POLINÓMICAS

21. Observamos los signos del polinomio y concluimos que la solución es el
conjunto
−∞, −1 ∪ 3,5
−1 3 5
𝑥 + 1
𝑥 − 3
𝑥 − 5
𝑥 + 1 𝑥 − 3 𝑥 − 5
− + + +
− − + +
− − − +
− + − +
Al descomponer el polinomio se obtiene
𝑥3 − 7𝑥2 + 7𝑥 + 15 = 𝑥 + 1 · 𝑥 − 3 · 𝑥 − 5
Formamos la tabla y calculamos los signos:
Resuelve la inecuación 𝑥3
− 7𝑥2
+ 7𝑥 + 15 ≤ 0
INECUACIONES POLINÓMICAS

22. En el primer caso la solución es 1 ∪ 3, ∞
En el segundo caso la solución es 1, ∞
En el tercer caso la solución es −∞, 0 ∪ 2,4
Resuelve las inecuaciones 𝑝 𝑥 ≥ 0, donde 𝑝 𝑥 es el polinomio dado
por las siguientes gráficas en cada caso.
INECUACIONES POLINÓMICAS

23. 
Igual que en las inecuaciones polinómicas, vamos a resolverlas cuando
estén en la forma
𝑝 𝑥
𝑞 𝑥
≥ 0
Para resolverlas, calcularemos los signos del numerador y del
denominador para así calcular los signos del cociente.
El cálculo de los signos se hace del mismo modo que en las ecuaciones
polinómicas.
INECUACIONES RACIONALES

24. En la solución, añadimos el punto en el que el numerador se hace cero,
y quitamos el punto en el que el denominador se hace cero porque no
se puede dividir entre cero. La solución es −∞, −3 ∪ 3, ∞
−∞, −3 − 3 −3,3 3 3, ∞
𝑥 − 3 − − +
𝑥 + 3 − + +
𝑥 − 3
𝑥 + 3
+ − +
Ejemplo: Si tuviéramos la inecuación
𝑥 − 1
𝑥 + 3
≥
2
𝑥 + 3
⇔
𝑥 − 1
𝑥 + 3
−
2
𝑥 + 3
≥ 0 ⇔
𝑥 − 3
𝑥 + 3
≥ 0
Para resolver, calcularemos los signos de numerador y denominador,
exactamente de la misma forma que en las inecuaciones polinómicas,
para hallar el signo del cociente:
INECUACIONES RACIONALES

25. Nota: En general
• Si la desigualdad contiene el símbolo igual: incluimos los ceros del
numerador y excluimos los ceros del denominador.
• Si la desigualdad es estricta: excluimos todos los ceros, tanto del
numerador como del denominador.
−∞, −3 − 3 −3,3 3 3, ∞
𝑥 − 3 − − +
𝑥 + 3 − + +
𝑥 − 3
𝑥 + 3
+ − +
Si la inecuación hubiera sido
𝑥 − 3
𝑥 + 3
> 0
En la solución se hubieran quitado los dos extremos: −∞, −3 ∪ 3, ∞
INECUACIONES RACIONALES

26. −1 3 5
𝑥 + 1
𝑥 − 3
𝑥 − 5
𝑥 − 3
𝑥 + 1 𝑥 − 5
− + + +
− − + +
− − − +
− + − +
Descomponemos el denominador (el numerador ya es de grado 1)
𝑥2 − 4𝑥 − 5 = 𝑥 + 1 𝑥 − 5
Formamos la tabla y calculamos los signos:
Resuelve la inecuación
𝑥 − 3
𝑥2 − 4𝑥 − 5
≤ 0
INECUACIONES RACIONALES
Observamos los signos del polinomio y concluimos que la solución es el
conjunto
−∞, −1 ∪ 3, 5

27. 
Una inecuación lineal de dos incógnitas es una inecuación del tipo:
2𝑥 + 3𝑦 ≤ 6
Y las soluciones serán pares 𝑥, 𝑦 que verifiquen la desigualdad.
Interpretaremos los pares 𝑥, 𝑦 como puntos del plano, así que las
soluciones de la inecuación serán puntos del plano que verifiquen la
desigualdad.
Para descubrir cuáles serán dichos puntos del plano, la solución se dará
de forma gráfica, y para ello realizaremos los siguientes pasos:
INECUACIONES LINEALES
DE DOS INCÓGNITAS

28. 1. Representaremos gráficamente la ecuación
2𝑥 + 3𝑦 = 6
Que sabemos que es una recta del plano.
Esta recta nos dividirá el plano en dos partes, o dos semiplanos.
Para todos los puntos de uno de los dos semiplanos la desigualdad
se verificará.
2. Evaluaremos la desigualdad en un punto que NO esté en la recta, y
que sea sencillo.
• Si la desigualdad se cumple para ese punto en cuestión,
entonces la desigualdad será cierta para todos los puntos de ese
semiplano
• Si la desigualdad es falsa para ese punto en cuestión, también
será falsa para el resto de los puntos del semiplano
INECUACIONES LINEALES
DE DOS INCÓGNITAS

29. (Si la recta pasara por el 0,0 los valores que se darían serían otros.
Además, siempre vamos a procurar que las coordenadas me queden
enteras para que su representación sea más sencilla)
2𝑥 + 3 · 0 = 6 ⇒ 𝑥 = 3
2 · 0 + 3𝑦 = 6 ⇒ 𝑦 = 2
x y
𝟎
𝟎 𝟐
𝟑
Para la primera parte, representar la recta, observamos que una
ecuación lineal de dos incógnitas es una recta del plano. Así que para
representarla gráficamente solo necesitamos calcular dos puntos por
los que pase dicha recta. Eso se hace dando dos valores fáciles:
INECUACIONES LINEALES
DE DOS INCÓGNITAS

30. Nota: Además, en este caso,
como la desigualdad contenía el
símbolo igual, la recta debe estar
incluida como solución: hay que
pensar que los puntos de la recta
son los puntos en los que se
verifica la igualdad.
Para la segunda parte, el punto más fácil para evaluar la inecuación es el
0,0 .
En este caso nos queda
0,0 ⇒ 2 · 0 + 3 · 0 ≤ 6
Que es cierto. Entonces todos los puntos que están del mismo lado de
la recta que el 0,0 forman parte de la solución. Es decir:
INECUACIONES LINEALES
DE DOS INCÓGNITAS

31. 
Si la recta pasara por 0,0 , escogeríamos un punto de uno de los ejes
de coordenadas para hacer la evaluación. Siempre debemos tener en
cuenta dos detalles:
 Debemos tener muy claro en que lado de la recta está el punto en el
que vamos a realizar la evaluación. Un punto ambiguo, que no sepa
si está encima o debajo, a la derecha o a la izquierda de la recta no
nos sirve.
 Escogeremos un punto que sea sencillo de evaluar, con coordenadas
enteras y pequeñas.
INECUACIONES LINEALES
DE DOS INCÓGNITAS

32. Un sistema de inecuaciones es un conjunto de inecuaciones. Puede ser
cualquier número de inecuaciones de cualquier tipo. Para resolver un
sistema:
• Se resuelve por separado cada una de las inecuaciones que forman
el sistema y se representa gráficamente su solución
• Una vez tenemos la solución de todas las inecuaciones que forman
el sistema, buscamos los puntos comunes a todas las inecuaciones a
la vez.
Si por ejemplo el siguiente gráfico mostrara la solución de las diversas
inecuaciones de un sistema
La solución serían los puntos comunes a las tres inecuaciones a la vez:
SISTEMAS DE INECUACIONES

33. En un sistema de inecuaciones lineales de dos incógnitas, deberemos
hallar los vértices de la figura resultante, lo que se hará resolviendo los
sistemas de ecuaciones lineales formados por las ecuaciones de las
rectas que definan cada uno de los vértices de la figura.
En este ejemplo la solución es el
triángulo.
En el caso de ser sistemas de
inecuaciones lineales de dos
incógnitas, las soluciones se deben
representar en los mismos ejes de
coordenadas para buscar los
puntos comunes:
SISTEMAS DE INECUACIONES

34. Vemos que el sistema no tiene solución puesto que no hay puntos
comunes a las dos soluciones. Su solución es ∅ (conjunto vacío)
Resolvemos la segunda inecuación. Operamos y descomponemos:
𝑥 + 1 𝑥 + 5 < 5 ⇔ 𝑥2
+ 6𝑥 + 5 − 5 < 0 ⇔ 𝑥2
+ 6𝑥 < 0
𝑥2
+ 6𝑥 < 0 ⇔ 𝑥 𝑥 + 6 < 0
Calculando los signos se tiene la solución
Resolvemos la primera inecuación y lo representamos gráficamente:
𝑥 + 1 > 10 ⇔ 𝑥 > 10 − 1 ⇔ 𝑥 > 9
Resolver el sistema
𝑥 + 1 > 10
𝑥 + 1 𝑥 + 5 < 5
SISTEMAS DE INECUACIONES

35. 0,0 ⇒ 3 · 0 + 0 > 2
3 · 1 + 𝑦 = 2 ⇒ 𝑦 = −1
3 · 0 + 𝑦 = 2 ⇒ 𝑦 = 2
x y
−𝟏
𝟎 𝟐
𝟏
0,0 ⇒ 0 − 2 · 0 ≤ 1
𝑥 − 2 · 0 = 1 ⇒ 𝑥 = 1
3 − 2𝑦 = 1 ⇒ 𝑦 = 1
x y
𝟎𝟏
𝟏𝟑
Resolvemos cada inecuación por separado, representando las
soluciones en los mismos ejes de coordenadas
Representamos primero la primera inecuación:
Resolver
𝑥 − 2𝑦 ≤ 1
3𝑥 + 𝑦 > 2
SISTEMAS DE INECUACIONES