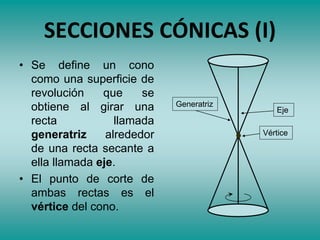
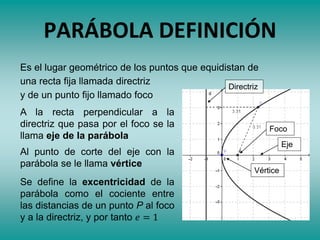
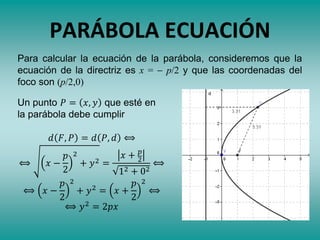
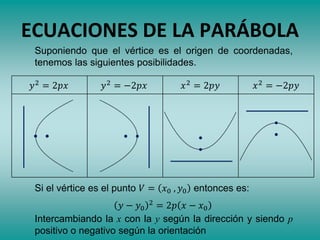
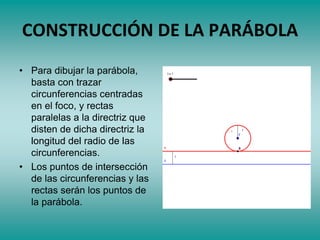
Este documento describe las secciones cónicas, incluyendo la definición y propiedades de la parábola. Explica que una parábola es el lugar geométrico de los puntos que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz. También proporciona métodos para construir y dibujar parábolas, así como ejemplos de su uso en antenas parabólicas y otros dispositivos. Finalmente, presenta ejercicios de resolución de problemas relacionados con parábolas.

1. SECCIONES
CÓNICAS:
LA PARÁBOLA
Prof. Carlos A. Blanco

2. Eje
SECCIONES CÓNICAS (I)
• Se define un cono
como una superficie de
revolución que se
obtiene al girar una
recta llamada
generatriz alrededor
de una recta secante a
ella llamada eje.
• El punto de corte de
ambas rectas es el
vértice del cono.
Generatriz
Vértice

3. SECCIONES CÓNICAS (II)
Al intersecar un cono con un plano que no pase por el vértice, se
obtienen las diferentes cónicas no degeneradas. Llamamos  al
ángulo que forma la generatriz con el eje. Entonces, si  es el
ángulo que forma el plano con el eje, se tiene que:
1. Si el plano es perpendicular al eje
𝛽 = 90° se obtiene una
circunferencia.
2. Si 𝛼 < 𝛽 < 90° se obtiene una
elipse.
3. Si el plano es paralelo a la
generatriz 𝛽 = 𝛼 se obtiene una
parábola.
4. Si 𝛽 < 𝛼 se obtiene una hipérbola.
Circunferencia
Elipse
Parábola
Hipérbola
Imagen realizada a partir de otra tomada de es.wikipedia.org/wiki/Sección_cónica

4. SECCIONES CÓNICAS (III)
Un experimento que se puede realizar es apuntar con una
linterna a una pared en algo de oscuridad. La forma que
adoptará la luz de la linterna contra la pared, según la
inclinación que tenga la linterna, irá formando las distintas
secciones cónicas.

5. Es el lugar geométrico de los puntos que equidistan de
PARÁBOLA DEFINICIÓN
A la recta perpendicular a la
directriz que pasa por el foco se la
llama eje de la parábola
Al punto de corte del eje con la
parábola se le llama vértice
y de un punto fijo llamado foco
una recta fija llamada directriz
Eje
Vértice
Foco
Directriz
Se define la excentricidad de la
parábola como el cociente entre
las distancias de un punto P al foco
y a la directriz, y por tanto 𝑒 = 1

6. Para calcular la ecuación de la parábola, consideremos que la
ecuación de la directriz es x =  p/2 y que las coordenadas del
foco son (p/2,0)
PARÁBOLA ECUACIÓN
Un punto 𝑃 = 𝑥, 𝑦 que esté en
la parábola debe cumplir
𝑑 𝐹, 𝑃 = 𝑑 𝑃, 𝑑 ⟺
⟺ 𝑥 −
𝑝
2
2
+ 𝑦2 =
𝑥 + 𝑝
2
12 + 02
⟺
⟺ 𝑥 −
𝑝
2
2
+ 𝑦2
= 𝑥 +
𝑝
2
2
⟺
⟺ 𝑦2
= 2𝑝𝑥

7. ECUACIONES DE LA PARÁBOLA
Suponiendo que el vértice es el origen de coordenadas,
tenemos las siguientes posibilidades.
Si el vértice es el punto 𝑉 = 𝑥0 , 𝑦0 entonces es:
𝑦 − 𝑦0
2
= 2𝑝 𝑥 − 𝑥0
Intercambiando la x con la y según la dirección y siendo p
positivo o negativo según la orientación
𝑦2 = 2𝑝𝑥 𝑦2 = −2𝑝𝑥 𝑥2 = 2𝑝𝑦 𝑥2 = −2𝑝𝑦

8. CONSTRUCCIÓN DE LA PARÁBOLA
• Para dibujar la parábola,
basta con trazar
circunferencias centradas
en el foco, y rectas
paralelas a la directriz que
disten de dicha directriz la
longitud del radio de las
circunferencias.
• Los puntos de intersección
de las circunferencias y las
rectas serán los puntos de
la parábola.

9. LA PARÁBOLA CON EL
MÉTODO DEL JARDINERO
• Deslizamos un cartabón a lo largo de la directriz.
• En la parte superior atamos un extremo de un hilo de la
misma longitud que el cartabón y el otro extremo lo atamos al
foco de la parábola.
• Mantenemos el hilo tenso con un lapicero.
• La curva que se obtiene al deslizar es una parábola.

10. USOS DE LA PARÁBOLA
La parábola tiene la siguiente propiedad sorprendente:
• Un rayo paralelo al eje de simetría se refleja en la superficie
directamente hacia el foco y viceversa.
Así las parábolas se pueden usar para:
• Antenas (antena parabólica)
• Radares
• Concentrar los rayos solares para calentar un punto
• Los espejos dentro de faros y linternas
• etc

11. EJERCICIOS DE PARÁBOLAS
Hay dos tipos de ejercicios de parábolas:
El primer tipo de ejercicio trata de encontrar la ecuación de
la parábola a partir de unos datos determinados
El segundo tipo de ejercicio trata de encontrar los
elementos más destacados de la parábola y realizar un
dibujo aproximado a partir de la ecuación.
En este tipo de ejercicio, puede ser que nos den la
ecuación de la parábola en forma reducida (más fácil)
Ó puede ser que nos den la ecuación de la parábola en
forma desarrollada (más difícil)

12. EJERCICIO 1 DE PARÁBOLAS
Halla la ecuación de la parábola que tiene su foco en el punto
de F = (3,2) y su directriz es d  2x – 3 = 0
Para calcular la ecuación necesitamos conocer el
vértice y el parámetro 𝑝 = 𝑑 𝐹, 𝑑 El vértice será
el punto intermedio entre el foco y la directriz.
𝑝 = 𝑑 𝐹, 𝑑 =
2 · 3 − 3
22 + 02
=
3
2
Observando la posición de foco y directriz, y la distancia entre
ambos, el vértice es el punto 𝑉 = 3,2 − 3
4
, 0 = 9
4
, 2
La ecuación de la parábola es entonces
𝑦 − 2 2
= 3 𝑥 −
9
4
d
V
F

13. EJERCICIO 2 DE PARÁBOLAS
Para la parábola de ecuación 𝑥 + 3 2
= −4 𝑦 − 1 halla las
coordenadas del foco, del vértice y de la directriz.
A la vista de la ecuación, la parábola es de
la forma:
Asimismo, a la vista de la ecuación, ya
tenemos tanto el vértice como el parámetro:
𝑉 = −3,1 y 𝑝 = 2 ⇒ 𝑝
2
= 1
El Foco estará una unidad por debajo del vértice:
𝐹 = −3,1 − 1 = −3,0
La directriz, al ser paralela al eje x, tendrá por ecuación 𝑦 = 𝑘,
siendo k una unidad mayor que la ordenada del Vértice.
𝑦 = 1 + 1 ⇒ 𝑦 = 2

14. EJERCICIO 3 DE PARÁBOLAS
Para la parábola de ecuación 𝑦2
+ 8𝑥 − 2𝑦 − 15 = 0 halla las
coordenadas del foco, del vértice y de la directriz.
Completamos cuadrados para obtener la ecuación
reducida
A la vista de la ecuación, deducimos que:
𝑉 = 2,1 y 𝑝 = 4 ⇒ 𝑝
2
= 2
El Foco estará dos unidades a la izquierda del vértice:
𝐹 = 2 − 2,1 = 0,1
La directriz, al ser paralela al eje y, tendrá por ecuación 𝑥 = 𝑘,
siendo k dos unidades mayor que la abscisa del Vértice.
𝑥 = 2 + 2 ⇒ 𝑥 = 4
𝑦 − 1 2
= −8 𝑥 − 2

15. CONICAS Y ESFERAS DE DANDELIN
• En las siguientes imágenes se puede
observar que las secciones cónicas
cumplen las definiciones como lugares
geométricos.
• Las imágenes proceden de la página
http://www.aulamatematicas.org/Conicas/
ConicasSeccionesCono.htm
• Para saber más sobre las esferas de
Dandelin, clic aquí

16. CONICAS Y ESFERAS DE DANDELIN
𝑃𝐹 = 𝑃𝑀 = 𝐻𝑇 = 𝑅𝑄 = 𝑃𝐷