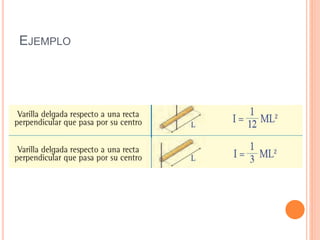
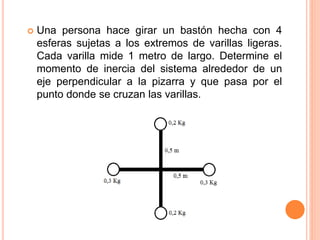
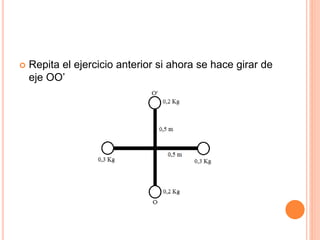
La inercia rotacional representa la resistencia de un cuerpo a cambiar su estado de movimiento rotatorio. Depende de factores como la masa, distribución de masa, dimensiones geométricas y posición del eje de rotación. La fórmula para calcular la inercia rotacional varía según la forma del cuerpo, pero generalmente involucra su masa y el radio desde el eje de rotación. Los ejemplos muestran cálculos de inercia rotacional y energía cinética para diferentes sistemas rotatorios y en movimiento.

1. INERCIA ROTACIONAL
III Medio

2. MASA INERCIAL
 Todos los cuerpos presentan una resistencia al
cambio de estado de movimiento, cuya intensidad
depende en cierta medida de la masa de ellos.
 La masa inercial es una medida de la resistencia
de un cuerpo a la aceleración.

3.  Los cuerpos que poseen mayor masa tienen más
inercia, ya que es más difícil cambiar su estado de
movimiento.

4. INERCIA ROTACIONAL
 Representa la propiedad de los cuerpos para
resistir los cambios de su estado de movimiento
rotatorio.
 Un cuerpo que rota alrededor de su eje tiende a
seguir rotando, a no ser que una fuerza externa
actúe sobre él.
 Un cuerpo que no rota tiende a seguir sin rotar.

5. FACTORES
 De sus dimensiones geométricas.
 De su masa.
 De la forma como está distribuida la masa; la
inercia aumenta en la medida que la distribución de
masa se aleja del eje de rotación.
 De la posición del eje alrededor del cual rota el
cuerpo.

6. INERCIA ROTACIONAL
 La inercia rotacional de un cuerpo de masa “M” que
gira alrededor de un eje describiendo un radio “r”
está dada por:
Como la inercia depende de la masa, de la distribución de la
masa, de la forma geométrica la fórmula de la Inercia
Rotacional varía de un cuerpo a otro. (Ver página 39)

7. EJEMPLO

8. EJERCICIOS
 Se hace girar un cuerpo de 500 gramos por medio
de una cuerda, determine cuánto vale la inercia
rotacional si:
 La cuerda mide 1,2 m
 La cuerda mide 1,8 m

9. Desde la parte superior de un plano inclinado se
sueltan dos esferas de 2 Kg de masa, la primera
tiene un radio de 30 cm y la segunda de 45 cm.
¿Cuál va acelerar con más facilidad?

10.  Determine la inercia rotacional de una varilla de 2,6
m de largo, 5 cm de diámetro y 4 Kg de masa, si:
 El eje de rotación está en el centro de la varilla
 El eje de rotación está en un extremo de la varilla.

11.  Una persona hace girar un bastón hecha con 4
esferas sujetas a los extremos de varillas ligeras.
Cada varilla mide 1 metro de largo. Determine el
momento de inercia del sistema alrededor de un
eje perpendicular a la pizarra y que pasa por el
punto donde se cruzan las varillas.

12.  Repita el ejercicio anterior si ahora se hace girar de
eje OO’

13. ENERGÍA CINÉTICA
 Cuando un cuerpo de masa “m” se traslada con
una rapidez “v” posee energía cinética, que está
dada por:
En el sistema de medida internacional la unidad de medida de la
energía es el “Joule” (J) que equivale a Kgm2/s2

14. ENERGÍA CINÉTICA ROTACIONAL
 En el caso de un cuerpo rígido que gira con una
rapidez angular de w, la energía está dada por:
En el caso de que un cuerpo se esté trasladando con una rapidez “v”
y además esté rotando en torno a un eje con una rapidez w, la
energía total corresponde a la suma de las energías cinéticas de
traslación (Ec) y la de rotación (Er)

15. EJEMPLO
 Un disco de 30 cm de radio y 2 kg de masa se
mueve por una superficie horizontal a 0,8 m/s y gira
a 2 Hz. Determine:
 Energía cinética traslacional
 Energía cinética rotacional
 Energía cinética total.

16. EJEMPLO
 Una pelota cae desde una altura 2 metros por un
plano inclinado de 30°. Determine con qué rapidez
llegará la pelota al extremo inferior del plano
inclinado.

17.  Una pelota de 30 cm de radio, cae rodando con
una frecuencia de 1 Hz, desde una altura 2 metros
por un plano inclinado de 30°. Determine con qué
rapidez llegará la pelota al extremo inferior del
plano inclinado.