Este documento contiene 12 ejercicios de cálculo integral resueltos. Cada ejercicio presenta un problema de integración definida y su solución paso a paso. Los ejercicios involucran funciones como polinomios, cuadráticas, cúbicas y funciones definidas por tramos, así como el cálculo de áreas delimitadas por curvas.

1. SOLUCIONES
EJERCICIOS INTEGRALES
Ejercicio nº 1.-
Sabiendo que la gráfica de f(x) es la siguiente:
Y
8
6
4
2
X
−8 −6 −4 −2 2 4 6 8
−2
−4
−6
Calcula:
6
∫ f (x)
−0
Solución:
• Vamos a distinguir dos recintos:
I [ 0, 4 ] , II [ 4, 6 ]
• El área del recinto I es:
4⋅3
= 6 u2 , ya que es un triángulo de base 4 y altura 3.
2
• El área del recinto II es:
2⋅3
= 3 u2 , ya que es un triángulo de base 2 y altura 3.
2
• Por tanto:
6
∫ f ( x ) = área recinto I − área recinto II = 6 − 3 = 3 u
2
0

2. Ejercicio nº 2.-
Dada la función f ( x ) = 2 x 2 − 3 x , calcula :
6
a) ∫ f (x)
0
0
b) ∫ f (x)
−1
Solución:
∫ ( 2x ) 2x 3 3x 2
• G( x ) = 2
− 3x = −
3 2
9 13
• G( 3) = ; G ( 0 ) = 0; G ( − 1) = −
2 6
3 9 9
a) ∫ f = G( 3) − G( 0) = 2 − 0 = 2
0
0
 13  13
b) ∫ G( 0 ) − G( − 1) = 0 −  − =
−1  6  6
Ejercicio nº 3.-
Halla el área del recinto limitado por la parábola f ( x ) = x 2 − x − 6 y el eje X en el
intervalo [0, 4]
Solución:
• Puntos de corte con el eje X:
1 ± 1 + 24  x1 = −2

x2 − x − 6 = 0 → x = = → 
2  x2 = 3

En el intervalo [0, 4] solo está x2 = 3.
• Hay dos recintos: I [0, 3]; II [3, 4]
∫ (x ) x3 x2
• G( x ) = 2
−x −6 = − − 6x
3 2
−27 −32
• G ( 0 ) = 0; G ( 3 ) = ; G( 4) =
2 3

3. 27
• Área del recinto I = G( 3) − G( 0 ) =
2
17
Área del recinto II = G ( 4 ) − G( 3 ) =
6
27 17 49 2
Área total = + = u
2 6 3
• La gráfica no es necesaria, pero la incluimos para visualizar el resultado:
Y
8
6
4
2
X
−8 −6 −4 −2 2 4 6 8
−2
−4
−6
f( x ) = x 2−x − 6
Ejercicio nº 4.-
Las siguientes gráficas corresponden a las funciones:
x3
y = x 3 − 2x e y =
2
Y
8
6
4
2
y = x 3−2 x
X
−8 −6 −4 −2 2 4 6 8
−2
−4
y= x3
2 −6
Calcula el área del recinto limitada por ellas.
Solución:

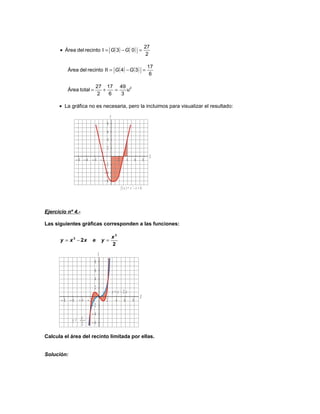
4. x3 x3
• x 3 − 2x − = − 2x
2 2
x3
2
− 2x = 0 → x 3 − 4x = 0 → ( )
x x2 − 4 = 0 → x1 = −2, x 2 = 0 , x 3 = 2 .
• Hay dos recintos: I [-2, 0]; II [0, 2]
 x3  x4
• G( x ) = 
 2 ∫
− 2x  =
 8 −x
2
 
• G ( − 2) = −2; G ( 0 ) = 0; G( 2) = −2
• Área del recinto I = G ( 0) − G ( − 2) = 2
Área del recinto II = G ( 2) − G ( 0) = 2
2
• Área total = 2 + 2 = 4u
Ejercicio nº 5-
Dada la gráfica de la función f (x):
Y
2 f(x )
1
I
X
−2 −1 1 2
II
−2
19 2
sabiendo que el área del recinto I es 2 u2 y que el área del recinto II es u , calcula :
2
2
∫ f (x)
−2
Solución:
2 19 − 15 2
∫ f ( x ) = área recinto I - área recinto II = 2 − = u
−2 2 2

5. Ejercicio nº 6.-
2
Calcula ∫ f ( x ), siendo :
0
 x 2 + 1 si 0 ≤ x < 1
f (x) = 
 2 si 1 ≤ x ≤ 2
Solución:
• Entre 0 y 1:
∫ (x ) x3
G1 ( x ) = 2
+1 = +x
3
4
G1 ( 1) = ; G1 ( 0 ) = 0
3
∫ (x )
1 4
2
+ 1 = G1 ( 1) − G1 ( 0 ) =
0 3
• Entre 1 y 2:
G2 ( x ) = 2 = 2 x
∫
G2 ( 2) = 4; G2 ( 1) = 2
2
∫ 2 = G2 ( 2) − G2 (1) = 4 − 2 = 2
1
• Por tanto:
2 4 10
∫ f ( x) = 3 + 2 =
0 3
Ejercicio nº 7.-
Calcula el área comprendida entre la función y = x 2 − 1 y el eje X en el intervalo [ 0, 2].
Solución:
• Puntos de corte con el eje X:
x2 −1 = 0 → x 1 = −1 , x 2 = 1

6. Solo nos sirve x = 1 en el intervalo [0, 2].
• Tenemos dos recintos:
I [0, 1]; II [1, 2]
∫ (x ) x3
• G( x ) = 2
−1 = −x
3
−2 2
• G ( 0 ) = 0; G (1) = ; G ( 2) =
3 3
2
• Área del recinto I = G (1) − G( 0 ) =
3
4
Área del recinto II = G ( 2) − G (1) =
3
2 4 6
Área total = + = = 2u2
3 3 3
• La gráfica no es necesaria; la incluimos para visualizar el resultado:
Y
3
2
1
II
X
−2 −1 I 1 2 3
−1
y = x 2− 1
Ejercicio nº 8.-
2
Halla el área comprendida entre la curva y = 2x + 2x - 1 y la recta y = 4x + 3.
Solución:
• 2x 2 + 2x − 1 − ( 4 x + 3 ) = 2 x 2 − 2 x − 4
1± 1+ 8  x1 = −1

• 2x 2 − 2x − 4 = 0 → x2 − x − 2 = 0 → x= → 
2  x2 = 2


7. ∫ ( 2x ) 2x 3
• G( x ) = 2
− 2x − 4 = − x 2 − 4x
3
7 −20
• G( − 1) = ; G ( 2) =
3 3
• Área = G( 2) − G( − 1) = 9 u2
• Las gráficas no son necesarias, pero las incluimos para visualizar el resultado:
Y
10
8
6
4
2
X
−8 −6 −4 −2 2 4 6 8
−2
y=4x+3
y = 2 x 2+ 2 x − 1
Ejercicio nº 9.-
La gráfica de una cierta función, f(x) , es la siguiente:
Y
8
6
4
2
X
−8 −6 −4 −2 2 4 6 8
−2
−4
−6
A partir de esta gráfica, calcula:
4
∫ f (x)
0
Solución:
• Vamos a distinguir dos recintos:
I [ 0, 3 ] , II [ 3, 4 ]

8. • El área del recinto I, que es un trapecio, es:
( 3 + 2) ⋅ 3 = 15 u 2
2 2
El área del recinto II, que es un triángulo, es:
1⋅ 3 3 2
= u
2 2
•..Por tanto:
4 15 3 12
∫ f ( x ) = área del recinto I − área del recinto II =
0 2
−
2
=
2
= 6 u2
Ejercicio nº 10.-
Resuelve la siguiente integral:
∫ ( 2x )
3
2
+3
1
Solución:
∫ ( 2x ) 2x 3
• G( x ) = 2
+3 = + 3x
3
11
• G( 3 ) = 27; G( 1) =
3
∫ ( 2x )
3 11 70
• 2
+ 3 = G ( 3) − G( 1) = 27 − =
1 3 3
Ejercicio nº 11.-
Halla el área limitada por la función y = x 3 + x 2 − 2 x y el eje X .
Solución:
• Puntos de corte con el eje X:
x1 = 0
3 2 
x + x − 2x = 0 → x x + x − 2 = 0 → ( 2
)
− 1± 1+ 8 − 1± 3 x = 1
x = 2
=
2
→  2
 x3 = −2

• Hay, entonces, dos recintos:

9. I [ − 2, 0 ] ; II [ 0, 1 ]
∫ (x ) x4 x3
• G( x ) = 3
+ x 2 − 2x = + − x2
4 3
8 −5
• G ( − 2) = − ; G ( 0 ) = 0; G(1) =
3 12
8
• Área del recinto I = G ( 0 ) − G ( − 2) =
3
5
Área del recinto II = G(1) − G( 0) =
12
8 5 37 2
• Área total = + = u
3 12 12
• La gráfica no es necesaria, pero la incluimos para visualizar el resultado:
Y
4
2
X
−4 −2 2 4
−2
y = x 3+ x 2− 2 x
Ejercicio nº 12.-
Calcula el área del recinto limitado por las curvas y = x 2 − 1 e y = 1 − x 2 .
Solución:
(
• x 2 − 1 − 1 − x 2 = 2x 2 − 2)
• 2x 2 − 2 = 0 → x1 = −1 , x 2 = 1
∫ ( 2x ) 2x 3
• G( x ) = 2
−2 = − 2x
3
4 −4
• G ( − 1) = ; G (1) =
3 3

10. 8 2
• Área = G (1) − G ( − 1) = u
3
Las gráficas no son necesarias, pero las incluimos para visualizar el resultado:
Y
y = x 2− 1
2
1
X
−2 −1 1 2
−1
−2 y= 1−x2
Ejercicio nº 13-
Halla el área del recinto limitado por la función f ( x ) = x 3 − 4 x y el eje X .
Solución:
• Puntos de corte con el eje X:
x 3 − 4x = 0 → (
x x2 − 4 = 0 ) → x1 = −2, x 2 = 0, x 3 = 2
• Hay dos recintos : I [ − 2, 0 ] ; II [ 0, 2 ]
∫ (x ) x4
• G( x ) = 3
− 4x = − 2x 2
4
• G ( − 2) = −4; G ( 0 ) = 0; G ( 2) = −4
• Área del recinto I = G ( 0 ) − G ( − 2) = 4
Área del recinto II = G ( 2) − G ( 0 ) = 4
2
• Área total = 4 + 4 = 8 u
• La gráfica no es necesaria, pero la incluimos para visualizar el resultado:

11. Y
4
2
X
−4 −2 2 4
−2
f( x ) = x 3− 4 x
Ejercicio nº 14.-
2
Calcula el área limitada por la parábola y = x +1, la recta y = 4x -3 y el eje Y.
Solución:
• x 2 + 1 − ( 4 x − 3) = x 2 − 4x + 4
x 2 − 4x + 4 = 0 → x=2
Hay un recinto [0, 2].
∫ (x ) x3
• G( x ) = 2
− 4x + 4 = − 2x 2 + 4x
3
8
• G ( 2) = ; G( 0) = 0
3
8 2
• Área = G ( 2) − G ( 0) = u
3
• Las gráficas no son necesarias, pero las incluimos para visualizar el resultado:
Y
10
8
6
4
2
X
−8 −6 −4 −2 2 4 6 8
−2 y= 4x−3
y = x 2+ 1

12. Ejercicio nº 15.-
Calcula:
1 4 
 − x + 2x 2 
∫  3
0


Solución:
 − x4  − x 5 2x 3
• G( x ) = 
 3∫ + 2x 2  =
 +
  15 3
3
• G (1) = ; G( 0) = 0
5
1 − x4 2 3
∫  3 + 2 x  = G(1) − G ( 0 ) = 5
•  
0 
Ejercicio nº 16.-
Calcula el área comprendida entre la función y = x 2 + 2 x + 3, el eje X y las rectas x = − 1 y x = 1.
Solución:
• Puntos de corte con el eje X:
− 2 ± 4 − 12
x 2 + 2x + 3 = 0 → x=
2
No corta al eje X.
∫ (x ) x3
• G( x ) = 2
+ 2x + 3 = + x 2 + 3x
3
−7 13
• G ( − 1) = ; G (1) =
3 3
20 2
• Área = G (1) − G ( − 1) = u
3
• La gráfica no es necesaria, pero la incluimos para visualizar el resultado:

13. Y
6
4
2
X
−4 −2 2 4
f( x ) = x 2+ 2 x + 3
Ejercicio nº 17.-
Calcula el área comprendida entre las curvas y = 2 x 2 − 5 x , y = x 2 − 2x y x = −1.
Solución:
(
• 2x 2 − 5 x − x 2 − 2x = x 2 − 3 x )
• x − 3x = 0
2
→ x1 = 0, x 2 = 3
• Hay dos recintos: I [-1, 0]; II [0, 3]
∫ (x ) x 3 3x 2
• G( x ) = 2
− 3x = −
3 2
−11 −9
• G( − 1) = ; G ( 0 ) = 0; G ( 3 ) =
6 2
11
• Área del recinto I = G ( 0 ) − G ( − 1) =
6
9
• Área del recinto II = G ( 3) − G ( 0 ) =
2
11 9 19 2
• Área total = + = u
6 2 3
• Las gráficas no son necesarias, pero las incluimos para visualizar el resultado:
Y
10
8
6
4 y = x 2− 2 x
2
X
−8 −6 −4 −2 2 4 6 8
−2
−4 y = 2 x 2−5 x