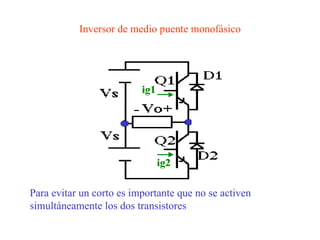
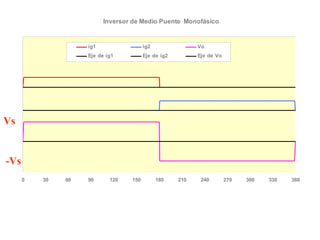
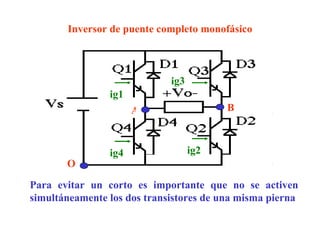
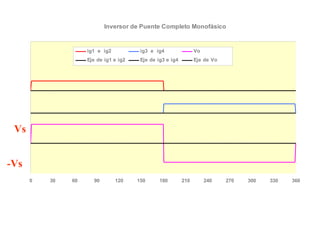
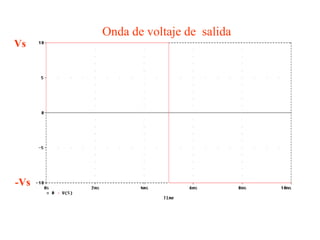
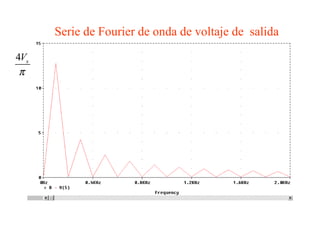
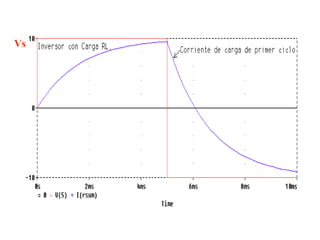
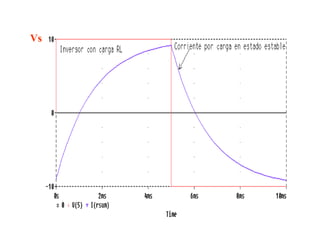
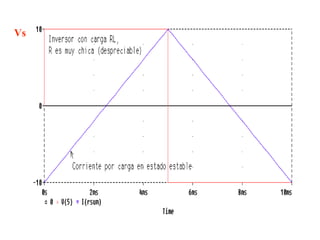
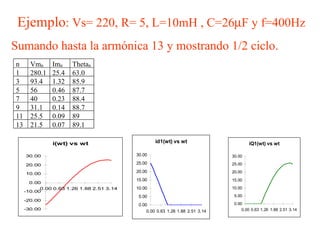
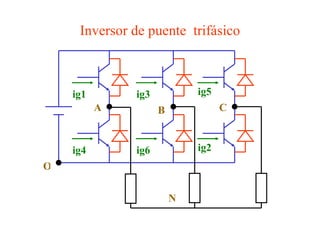
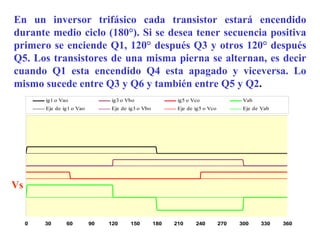
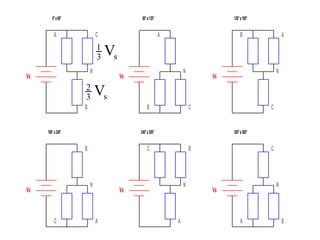
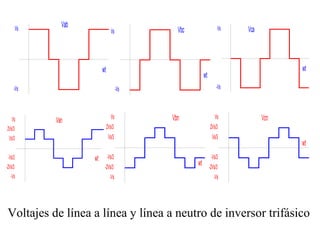
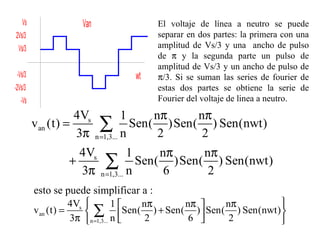
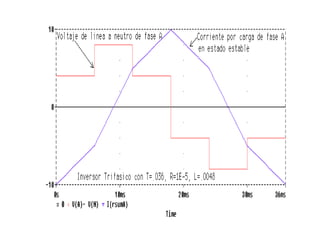
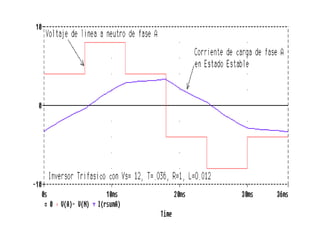
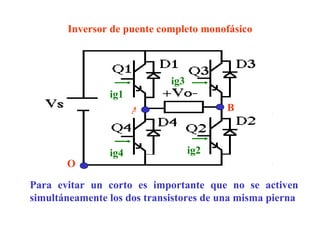
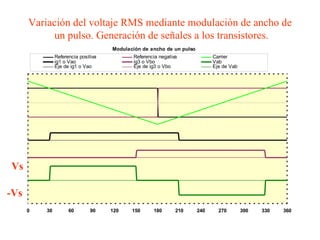
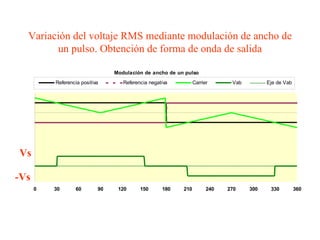
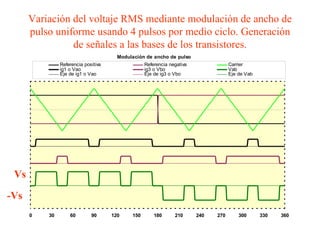
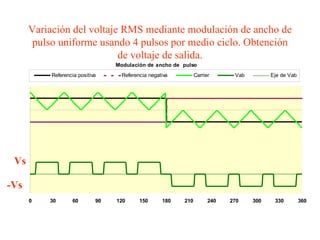
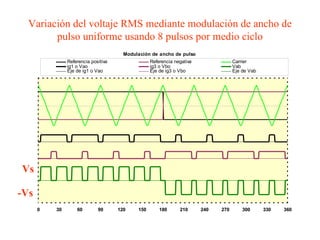
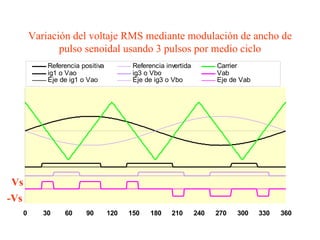
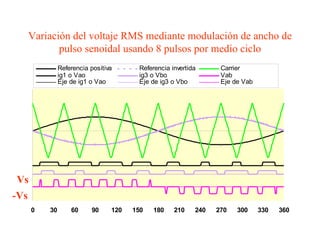
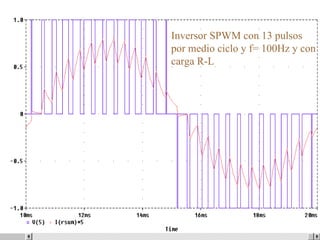
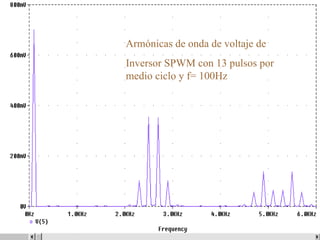
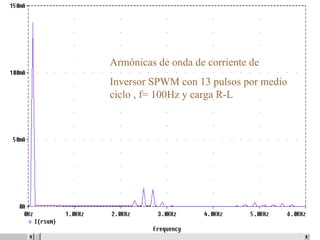
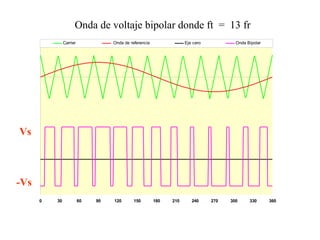
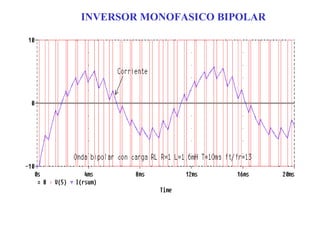
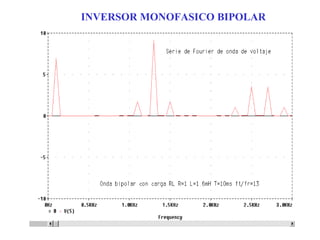
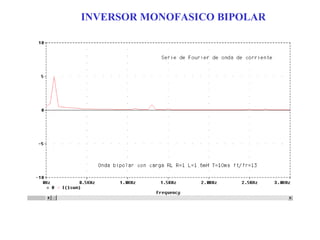
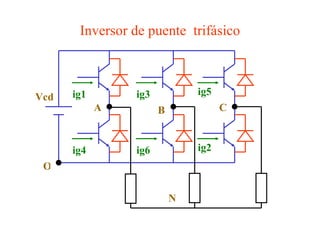
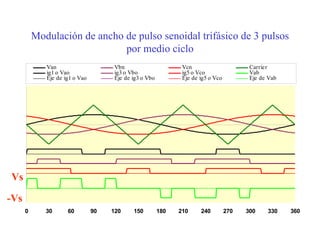
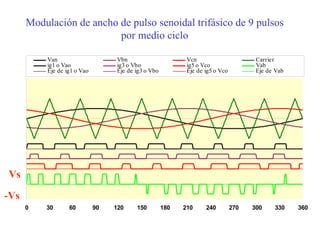
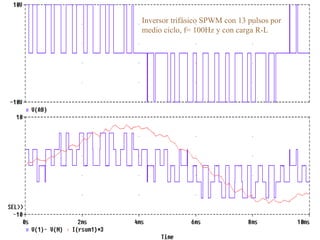
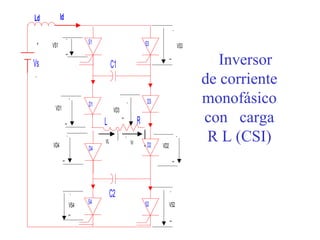
Este documento describe los diferentes tipos de convertidores de corriente directa a corriente alterna (inversores), incluyendo inversores monofásicos, trifásicos y las técnicas de modulación de ancho de pulso para variar el voltaje de salida. Explica conceptos como serie de Fourier, armónicas y formas de onda de voltaje y corriente de salida para diferentes configuraciones de inversores.

1. Convertidores de Corriente Directa a Corriente Alterna o Inversores ITESM, Ingeniería Eléctrica Ing. Javier Rodríguez Bailey

2. Inversor de medio puente monofásico Para evitar un corto es importante que no se activen simultáneamente los dos transistores

3. Vs -Vs

4. Armonica de menor orden(LOH)= es la armonica mas cercana a la fundamental cuya amplitud sea mayor o igual a 3% de fundamental Serie de Fourier de Vo

5. Inversor de puente completo monofásico Para evitar un corto es importante que no se activen simultáneamente los dos transistores de una misma pierna A B O ig1 ig3 ig4 ig2

6. Vs -Vs

7. modulación de ancho de pulso uniforme(pulsos=1) .param per=10m pul= 1 M=1 vtri 1 0 pulse(10,-10,0,{per/(pul*2)},{per/(pul*2)},.1u,{per/pul+.2u}) vcua 2 0 pulse({-10*M},{10*m},0,1u,1u,{per/2},{per+2u}) ecom1 3 0 table {v(2)-v(1)} (0 0) (1u 10) ecom2 4 0 table {-v(2)-v(1)} (0 0) (1u 10) esum 5 0 value = {v(3)-v(4)} rsum 5 6 1.0 lsum 6 0 .0016 rcom2 4 0 1 rcom1 3 0 1 rtri 1 0 1 rsin 2 0 1 .probe .tran .1m 10m .end Simulación de un inversor monofásico en Pspice

8. Onda de voltaje de salida Vs -Vs

9. Serie de Fourier de onda de voltaje de salida

10. Vs

11. Vs

12. Vs

13. Determinación de la serie de Fourier de un pulso en forma generalizada

14. Usemos los resultados anteriores para obtener la serie de Fourier del pulso mostrado en la figura. Las diferencias importantes son que este es negativo y defasado 180°.

15. Sumemos los resultados anteriores para obtener la serie de Fourier de la siguiente onda.

16. Al sumar los dos pulsos la forma de onda tiene simetría de media onda y por esta razón desaparecen todas las armónicas pares. La ecuación final de este pulso de amplitud uno es: Simplificando: Si es una onda cuadrada de amplitud Vs:  = 0 y 

17. Para determinar la forma de onda de la corriente se puede utilizar la serie de Fourier de voltaje y para cada término de la serie de Fourier de voltaje determinar el término correspondiente de corriente. Por ejemplo si suponemos una carga R L C en serie.

18. Ejemplo : Vs= 220, R= 5, L=10mH , C=26  F y f=400Hz Sumando hasta la armónica 13 y mostrando 1/2 ciclo.

19. Inversor de puente trifásico ig1 ig3 ig5 ig4 ig6 ig2 A B C O N

20. En un inversor trifásico cada transistor estará encendido durante medio ciclo (180°). Si se desea tener secuencia positiva primero se enciende Q1, 120° después Q3 y otros 120° después Q5. Los transistores de una misma pierna se alternan, es decir cuando Q1 esta encendido Q4 esta apagado y viceversa. Lo mismo sucede entre Q3 y Q6 y también entre Q5 y Q2 . Vs

22. Voltajes de línea a línea y línea a neutro de inversor trifásico

23. Serie de Fourier para el voltaje Vab adelantando el eje 30 grados:  y  y amplitud es Vs Y si se reemplaza wt´= wt+  /6) se obtiene: Usando:

24. El voltaje de línea a neutro se puede separar en dos partes: la primera con una amplitud de Vs/3 y una ancho de pulso de  y la segunda parte un pulso de amplitud de Vs/3 y un ancho de pulso de  /3. Si se suman las series de fourier de estas dos partes se obtiene la serie de Fourier del voltaje de linea a neutro. esto se puede simplificar a :

27. El Inversor además de variar la frecuencia puede variar el voltaje RMS de salida usando las técnicas de modulación de ancho de pulso: Modulación de ancho de un pulso Modulación de ancho uniforme de varios pulsos Modulación senoidal de ancho de varios pulsos

28. Inversor de puente completo monofásico Para evitar un corto es importante que no se activen simultáneamente los dos transistores de una misma pierna A B O ig1 ig3 ig4 ig2

29. Variación del voltaje RMS mediante modulación de ancho de un pulso. Generación de señales a los transistores. Vs -Vs

30. Variación del voltaje RMS mediante modulación de ancho de un pulso. Obtención de forma de onda de salida Vs -Vs

31. Ac = Amplitud de la onda carrier (triangular) Ar = Amplitud de la onda de referencia (cuadrada) M= Indice de modulación = Ar/Ac ft= frecuencia de onda triangular fr= frecuencia de onda de referencia p= número de pulsos por medio ciclo= ft/fr  = ancho del pulso= M  /p Modulación de ancho de pulso uniforme

32. Variación del voltaje RMS mediante modulación de ancho de pulso uniforme usando 4 pulsos por medio ciclo. Generación de señales a las bases de los transistores. Vs -Vs

33. Variación del voltaje RMS mediante modulación de ancho de pulso uniforme usando 4 pulsos por medio ciclo. Obtención de voltaje de salida. Vs -Vs

34. Variación del voltaje RMS mediante modulación de ancho de pulso uniforme usando 8 pulsos por medio ciclo Vs -Vs

35. Variación del voltaje RMS mediante modulación de ancho de pulso senoidal usando 3 pulsos por medio ciclo Vs -Vs

36. Variación del voltaje RMS mediante modulación de ancho de pulso senoidal usando 8 pulsos por medio ciclo Vs -Vs

37. Simulación (usando Pspice) de un inversor usando la técnica de Modulación de ancho de pulso senoidal (SPWM), su contenido de armónicas de voltaje así como las de corriente cuando se tiene una carga R-L Se uso una frecuencia de 100 HZ y 13 pulsos por medio ciclo ITESM, Ingeniería Eléctrica Ing. Javier Rodríguez Bailey

38. modulación de ancho de pulso senoidal .param per=10m pul= 13 vtri 1 0 pulse(10,10,0,{per/(pul*2)},{per/(pul*2)},.1u,{per/pul+.2u}) vsen 2 0 sin(0,7,{1/per},0,0,0) ecom1 3 0 table {v(2)-v(1)} (0 0) (1u 1.0) ecom2 4 0 table {-v(2)-v(1)} (0 0) (1u 1.0) esum 5 0 value = {v(3)-v(4)} rsum 5 6 5.0 lsum 6 0 .0016 rcom2 4 0 1 rcom1 3 0 1 rtri 1 0 1 rsin 2 0 1 .probe .four 100 30 v(5) i(rsum) .tran .1m 20m .end

39. Inversor SPWM con 13 pulsos por medio ciclo y f= 100Hz y con carga R-L

40. Armónicas de onda de voltaje de Inversor SPWM con 13 pulsos por medio ciclo y f= 100Hz

41. Armónicas de onda de corriente de Inversor SPWM con 13 pulsos por medio ciclo , f= 100Hz y carga R-L

42. FOURIER COMPONENTS OF TRANSIENT RESPONSE V(5) DC COMPONENT = -9.900990E-03 HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG) 1 1.000E+02 7.185E-01 1.000E+00 -1.338E+00 0.000E+00 2 2.000E+02 5.403E-02 7.521E-02 -1.708E+02 -1.695E+02 3 3.000E+02 1.111E-02 1.546E-02 1.117E+01 1.250E+01 4 4.000E+02 8.027E-02 1.117E-01 8.798E+00 1.014E+01 5 5.000E+02 2.447E-02 3.405E-02 4.968E+01 5.102E+01 6 6.000E+02 1.935E-02 2.693E-02 8.765E+01 8.899E+01 7 7.000E+02 1.550E-02 2.158E-02 1.145E+02 1.158E+02 8 8.000E+02 2.095E-02 2.916E-02 1.262E+01 1.396E+01 9 9.000E+02 3.394E-02 4.724E-02 -1.079E+01 -9.451E+00 10 1.000E+03 5.708E-02 7.945E-02 -1.559E+01 -1.426E+01 11 1.100E+03 2.065E-02 2.874E-02 -1.079E+02 -1.066E+02 12 1.200E+03 1.926E-02 2.681E-02 -6.877E+01 -6.743E+01 13 1.300E+03 4.131E-02 5.749E-02 -1.512E+01 -1.378E+01 14 1.400E+03 3.037E-02 4.227E-02 -5.811E-01 7.571E-01 15 1.500E+03 1.520E-02 2.116E-02 4.242E+01 4.375E+01 16 1.600E+03 5.031E-02 7.002E-02 2.058E+01 2.192E+01 17 1.700E+03 3.914E-02 5.448E-02 1.498E+02 1.511E+02 18 1.800E+03 1.257E-01 1.750E-01 7.185E+00 8.523E+00 19 1.900E+03 1.318E-02 1.835E-02 3.173E+01 3.307E+01 20 2.000E+03 1.019E-02 1.418E-02 -2.297E+01 -2.163E+01 21 2.100E+03 2.314E-02 3.220E-02 -3.622E+01 -3.488E+01 22 2.200E+03 4.675E-02 6.507E-02 -1.558E+02 -1.544E+02 23 2.300E+03 1.426E-01 1.985E-01 -7.595E+00 -6.256E+00 24 2.400E+03 1.365E-02 1.900E-02 -1.109E+02 -1.095E+02 25 2.500E+03 3.393E-01 4.723E-01 -4.665E-01 8.717E-01 26 2.600E+03 4.223E-02 5.877E-02 1.102E+01 1.236E+01 27 2.700E+03 3.705E-01 5.156E-01 1.775E+02 1.788E+02 28 2.800E+03 8.493E-02 1.182E-01 1.665E+02 1.679E+02 29 2.900E+03 8.751E-02 1.218E-01 1.687E+02 1.701E+02 30 3.000E+03 2.912E-02 4.053E-02 1.616E+02 1.630E+02 TOTAL HARMONIC DISTORTION = 8.025821E+01 PERCENT

43. FOURIER COMPONENTS OF TRANSIENT RESPONSE I(rsum) DC COMPONENT = -3.668368E-04 HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG) 1 1.000E+02 1.372E-01 1.000E+00 -1.138E+01 0.000E+00 2 2.000E+02 3.915E-04 2.854E-03 7.326E+01 8.464E+01 3 3.000E+02 1.615E-04 1.177E-03 1.016E+02 1.130E+02 4 4.000E+02 3.037E-04 2.214E-03 1.307E+02 1.421E+02 5 5.000E+02 8.095E-05 5.901E-04 -1.336E+02 -1.223E+02 6 6.000E+02 6.844E-04 4.990E-03 9.150E+01 1.029E+02 7 7.000E+02 2.242E-04 1.635E-03 6.929E+01 8.067E+01 8 8.000E+02 1.063E-04 7.749E-04 1.002E+02 1.116E+02 9 9.000E+02 1.004E-04 7.317E-04 1.405E+02 1.519E+02 10 1.000E+03 5.297E-04 3.862E-03 -9.953E+01 -8.815E+01 11 1.100E+03 2.498E-05 1.821E-04 -3.499E+01 -2.362E+01 12 1.200E+03 2.585E-04 1.885E-03 -9.361E+01 -8.223E+01 13 1.300E+03 1.670E-04 1.217E-03 -1.689E+02 -1.575E+02 14 1.400E+03 1.021E-04 7.446E-04 1.347E+02 1.461E+02 15 1.500E+03 6.740E-05 4.914E-04 -1.030E+02 -9.165E+01 16 1.600E+03 4.393E-04 3.203E-03 1.008E+02 1.122E+02 17 1.700E+03 8.565E-05 6.244E-04 4.403E+01 5.540E+01 18 1.800E+03 7.571E-04 5.520E-03 1.051E+02 1.164E+02 19 1.900E+03 1.039E-04 7.573E-04 6.322E+01 7.460E+01 20 2.000E+03 5.318E-04 3.877E-03 -9.417E+01 -8.279E+01 21 2.100E+03 4.561E-04 3.325E-03 -8.879E+01 -7.741E+01 22 2.200E+03 3.052E-04 2.225E-03 -7.823E+01 -6.686E+01 23 2.300E+03 4.415E-03 3.219E-02 -8.285E+01 -7.148E+01 24 2.400E+03 5.063E-04 3.691E-03 8.997E+01 1.013E+02 25 2.500E+03 1.386E-02 1.011E-01 -8.272E+01 -7.134E+01 26 2.600E+03 2.287E-04 1.668E-03 -1.047E+02 -9.331E+01 27 2.700E+03 1.260E-02 9.183E-02 9.634E+01 1.077E+02 28 2.800E+03 8.370E-04 6.102E-03 -8.256E+01 -7.118E+01 29 2.900E+03 3.645E-03 2.657E-02 9.588E+01 1.073E+02 30 3.000E+03 7.137E-04 5.203E-03 -8.480E+01 -7.342E+01 TOTAL HARMONIC DISTORTION = 1.435519E+01 PERCENT

44. Todas las ondas de voltaje obtenidas para controlar el voltaje RMS han sido monopolares, es decir durante el primer medio ciclo los voltajes o son positivos o son cero y durante el segundo medio ciclo o son negativas o son cero. Otra alternativa es obtener una forma de onda bipolar, es decir que el voltaje en la carga cambie de positivo a negativo y luego otra vez positivo, cuidando que se tenga mas área positiva durante el primer medio ciclo y mas área negativa durante el segundo medio ciclo. Para lograr lo anterior los transistores Q1 y Q2 se activan juntos y alternan su operación con el par Q3 y Q4

45. Onda de voltaje bipolar donde ft = 13 fr Vs -Vs

46. INVERSOR MONOFASICO BIPOLAR

47. INVERSOR MONOFASICO BIPOLAR

48. INVERSOR MONOFASICO BIPOLAR

49. Inversor de puente trifásico Vcd ig1 ig3 ig5 ig4 ig6 ig2 A B C O N

50. Modulación de ancho de pulso senoidal trifásico de 3 pulsos por medio ciclo Vs -Vs

51. Modulación de ancho de pulso senoidal trifásico de 9 pulsos por medio ciclo Vs -Vs

52. Modulación de ancho de pulso senoidal en inversor trifásico * (pulsos =13) .param per=10m pul= 13 At=10 As=7 vtri T 0 pulse({At},{-At},{-per/(pul*4)},{per/(pul*2)},{per/(pul*2)},.1u,{per/pul+.2u}) vsenA A 0 sin(0,{As},{1/per},0,0,0) vsenB B 0 sin(0,{As},{1/per},0,0,-120) vsenC C 0 sin(0,{As},{1/per},0,0,120) econ1 1 0 table {v(A)-v(T)} (0 0) (1u 10) econ3 3 0 table {v(B)-v(T)} (0 0) (1u 10) econ5 5 0 table {v(C)-v(T)} (0 0) (1u 10) eAB AB 0 value = {v(1)-v(3)} eBC BC 0 value = {v(3)-v(5)} eCA CA 0 value = {v(5)-v(1)} * Carga R L conectada en estrella rsum1 1 11 1.0 lsum1 11 N .0016 rsum3 3 33 1.0 lsum3 33 N .0016 rsum5 5 55 1.0 lsum5 55 N .0016 * Resistencias usadas para * no dejar el nodo aislado rcon1 1 0 1 rcon3 3 0 1 rcon5 5 0 1 rab AB 0 1 rbc BC 0 1 rca CA 0 1 rtri T 0 1 rsina A 0 1 rsinb B 0 1 rsinc C 0 1 .probe .tran .1m 10m uic .end INVERSOR TRIFASICO

53. Inversor trifásico SPWM con 13 pulsos por medio ciclo, f= 100Hz y con carga R-L

54. Inversor de corriente monofásico con carga R L (CSI)

55. Inversor de Corriente (CSI) Los inversores de corriente en vez de usar una fuente de voltaje (VSI) usan una fuente de corriente. La fuente de corriente se implementa conectando en serie con una fuente de voltaje una inductancia que mantendrá la corriente constante. Inicialmente durante el medio ciclo positivo la corriente circula por Vs, Ld, S1, D1, L, R, D2 y S2. Los condensadores están cargados a un voltaje superior al de la carga (R Id). Al dispararse S3 y S4, los voltajes de los condensadores apagan a S1 y S2, obligando a la corriente a circular por Vs, Ld, S3, C1, D1,L, R, D2,C2 y S4. Los condensadores se descargan hasta un voltaje igual a la de la carga R Id y esto permite que conduzcan los diodos D3 y D4. Los condensadores C1 y C2 quedan en paralelo con la carga. Se inicia un transitorio donde la corriente gradualmente cambiara de sentido por la carga y ahora circulara por Vs, Ld, S3, D3, R, L, D4 y S4 iniciándose el medio ciclo negativo.