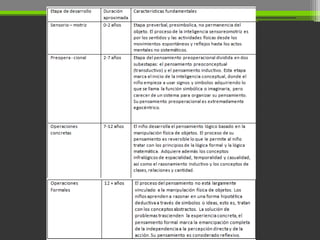
Este documento describe las diferentes etapas y habilidades necesarias para que los niños construyan el concepto de número. Explica que los niños nacen con la capacidad de razonar sobre lo numérico y que estudios muestran habilidades específicas como el conteo y las operaciones básicas. También discute teorías como la de Piaget sobre el desarrollo cognitivo a través de etapas cualitativas e incluye recomendaciones para ayudar a los niños a entender conceptos como igualdad, cantidad y representación numé

1. La construccion del numero
Integrantes:
Kathia Bonilla Limas
Stephanie Maldonado
Yara Martinez

2. Según investigaciones el niño nace con la capacidad de razonar sobre lo
numérico, y de manera precoz, pone estas habilidades a su disposición para
lograr el conocimiento y la organización del mundo que lo rodea.
Del mismo modo, los estudios realizados con niños arrojan importantes
hallazgos sobre habilidades específicas en la comprensión del número,
como por ejemplo, en el conteo, en las operaciones básicas y en el uso
inicial de las notaciones numéricas.
Durante muchos años, la propuesta de trabajar matemática en los primeros
años de escolaridad estuvo orientada por una concepción que trataba de
desarrollar y ejercitar la noción del número, presentándolo de uno en uno,
solo y de acuerdo con el orden de la serie numérica (ejercitación escrita
con trazado correcto), acompañada por la idea de que los niños no sabían
nada de los números y que para aprenderlos era conveniente hacerlo
desde el principio (1-2-3...)
Esto trajo como consecuencia, que el trabajo
didáctico se centrara sólo en los aspectos lógicos
del número como prerrequisito indispensable para
el trabajo numérico. Para que los niños y las niñas
descubran cómo funcionan los distintos sistemas
de notación y puedan operar con ellos, deben
utilizarlos en diversas situaciones, sin segmentaciones
artificiales impuestas por el adulto.

3. Fases a considerar para la
construcción del concepto de número
Fernández Bravo, expresa que para que el niño pueda interiorizar el concepto de
número se hace necesario pasar por distintas fases de diferente grado intelectual.
Por ello, el docente intencionará las siguientes:
a) Ayudar a entender que varias cosas distintas se pueden
llamar de la misma forma, es decir, por su propied numérica.
b) Posibilitar experiencias de aprendizaje que conlleve a la
identificación de un elemento elemento coordinable y,
mediante una correspondencia biunívoca entre éste y
los objetos, represente la propiedad numérica de distintos
grupos de objetos de igual cantidad, identificándola con el mismo nombre (uno,
dos, tres,…), para entenderlo como una clase de equivalencia.
c) Facilitar la asociación del nombre convencional (uno, dos, tres, …) a cualquier
grupo de objetos que pertenezca a esa clase.
d) Presentar el símbolo convencional con el que se sustituye la cantidad de
elementos coordinables: “1”; “2”; etc.
e) Asociar el símbolo con el nombre y con cualquier grupo de objeto de la misma
cantidad, que pertenezca a esa clase por su propiedad numérica.
f) Enseñar a responder a la pregunta cuántos. Cuando una cantidad de elementos
se mide por las veces de uno, lo que se obtiene es otro número por definición que
responde a la pregunta “cuantos”.

4. Necesitamos de algunos conocimientos
antes de introducirnos en el concepto de
número:
• Distinguir la parte del todo. Trabajar, en un principio, con
elementos que puedan verse como un todo en sí mismo.
(Evitar elementos que consten de varias partes; por ejemplo:
pinzas de la ropa, flores con pétalos, etc.).
• Reconocer elementos iguales y elementos
diferentes. Concepto intuitivo de igualdad
y de diferencia. Dos cosas son iguales
cuando entre ellas no hay diferencia
alguna. Dos cosas no son iguales cuando
alguna de ellas tiene al menos una
propiedad o característica que no
posee la otra.

5. • Establecer relaciones de clasificación, para que los niños vean que
existen, según criterios, elementos que poseen una misma
propiedad y elementos que no poseen esa propiedad comparar
intuitivamente el tamaño de dos agrupaciones de objetos,
mediante las expresiones: poco – muchos, o similares.
• Establecer correspondencia entre los elementos
de dos grupos de objetos, para reconocer
si hay, o no, “tantos elementos en un grupo
como en el otro”, y, en consecuencia saber
si hay, o no, “tantos elementos en un grupo
como en el otro”, y, en consecuencia, saber
si hay, o no, más elementos en uno que en otro.
• Representar la unicidad del elemento desde
el concepto de identidad: “Este bolígrafo”
es único en sí mismo, y yo no puedo enseñarte
“este bolígrafo” a no ser que tenga “este
bolígrafo”. Hay muchos bolígrafos iguales,
pero sólo cada uno es idéntico a sí mismo.
No carece de importancia diferenciar el
elemento en sí de otros varios iguales, o de
otros que tengan la misma propiedad- que
en nuestro ejemplo, sería “ser bolígrafo”

6. Destrezas de la cuantificación
Los niños pueden reconocer similitudes entre
cosas y recordar acontecimientos pasados,
aunque estos procesos son bastantes
complejo. Sin estas destrezas básicas, el
niño no podría aprender y desarrollarse con
ellas dispone de algunas herramientas
sorprendentemente generales para extraer
inferencias… Elizabeth Spelke

7. Las destrezas generales como la
lógica nos ha hecho considerar
la resolución de problemas de
una manera muy abstracta:
debido a que la lógica es una
base general para el
razonamiento.
Algunos investigadores creen que este conocimiento
“metacognitivo” (es decir,
conocimiento de los propios procesos mentales) es un
elemento clave en el desarrollo de la capacidad del niño
pequeño para desarrollar eficazmente destrezas a la hora de
solucionar problemas La resolución de problemas es una
actividad dinámica que recurre para disponer
convenientemente las destrezas y el conocimiento en
situaciones particulares.
El psicólogo ruco Lev Vygotsky propuso que la experiencia de
compartir la resolución de problemas con un compañero hábil
es uno de los principales métodos de adquisición de destrezas
de los niños. Vygotsky mostro que el nivel de destreza de un
niño puede producir es cuestion,e n gran parte, de cuanto
apoyo tiene de entorno (especialmente de otras personas)

8. Razonamiento Lógico
El desarrollo de las capacidades de razonamiento en los alumnos de educación
preescolar se propicia cuando despliegan sus capacidades para comprender el
problema, reflexionar lo que se busca, estimar posibles resultados, buscar distintas
vías de solución, comparar resultados, expresar ideas y explicarlas y confrontarlas
con sus compañeros. Ello no significa apresurar el aprendizaje formal de las
matemáticas con los niños pequeños si no potenciar las formas de pensamiento
matemático que poseen hacia el logro de las competencias que son
fundamento de conocimientos mas avanzados que irán construyendo a lo largo
de su escolaridad.
La actividad con las matemáticas alientan en los niños
la comprensión de nociones elementales y la aproximación
Reflexiva a nuevos conocimiento, así como las posibilidades
de verbalizar y comunicar los razonamientos que elaboran,
de revisar su propio trabajo y darse cuenta de lo que logran
o descubren durante sus experiencias de aprendizaje.
Ello contribuye además de la formación de actitudes
positivas hacia el trabajo en colaboración; el intercambio de
ideas con sus compañeros, considerando la opinión del otro
en relación con la propia; gusto hacia el aprendizaje;
autoestima y confianza en las propias capacidades.

9. Teoria del Desarrollo Cognoscitivo
Es una teoría que explica el funcionamiento de la mente
humana del cual uno de los principales exponentes es el
biólogo psicoanalista suizo Jean Peaget
La teoría del desarrollo intelectual adquiere una particular
importancia para la enseñanza – aprendizaje, que hace que
los principios básicos de la misma y sus consecuencias deban
ser conocidos por los profesores. Peaget establece que existe
un estrecho paralelismo entre el crecimiento físico y el
intelectual por lo que define la inteligencia como la
capacidad biológica del ser humano para adaptarse al
medio ambiente.
Piaget establece cuatro distintas etapas (estadios) en
términos de esquemas que son caracterizados por la forma
en la cual progresa el pensamiento al interactuar con su
medio ambiente social y físico. Esto quiere decir, que el niño
progresa atreves de cuatro distintas etapas cualitativas

11. Algunos conceptos claves que nos
ayudan a comprender mejor la teoría
de Piaget son:
• Un estadio se puede definir como un conjunto en particular de
característica física, emocional, intelectual o social del ser humano.
• Las operaciones concretas son acciones interiorizadas la cuales
pueden retornar al punto de partida y además puede ser
integradas a otras acciones que posean esta característica de
reversibilidad.
• El concepto de numero en imágenes o en la mera capacidad para
usar símbolos verbales, si no en la formación y sistematización en la
mente infantil de dos operaciones: la seriación y la clasificación
• En un error suponer que el niño adquiere la noción de número y
otros conceptos matemáticos solo de la enseñanza. Por el contrario
el niño los desarrolla el mismo, independiente y espontánea. Los
niños deben de comprender el principio de conservación de
cantidad antes de que puedan desarrollar el concepto de número

12. Bibliografía
• http://www.mec.gov.py/cms/adjuntos/2965?13
08950316 (p. 13-16)
• Programa de Educación Preescolar 2004 (p. 74)
• Difusión Educativa
Revista Trimestral de la Universidad Pedagógica
Nacional en Tamaulipas Abril 1994 (p. 14-15)