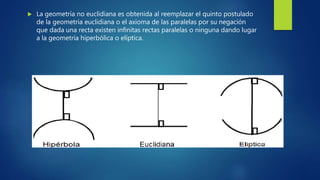
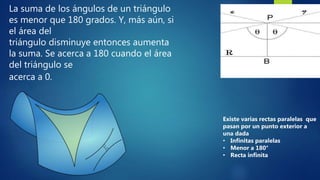
La geometría no euclidiana surge al reemplazar el quinto postulado de Euclides, conocido como el axioma de las paralelas. Esto da lugar a dos geometrías: la geometría hiperbólica, donde existen infinitas rectas paralelas a una dada que pasan por un punto exterior, y la geometría elíptica, donde la suma de los ángulos de un triángulo es menor que 180 grados y más rectas paralelas son posibles cuanto menor es el área del triángulo. Pioneros como Lobache