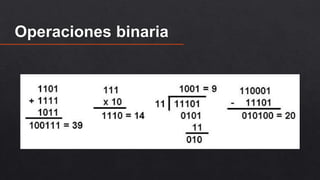
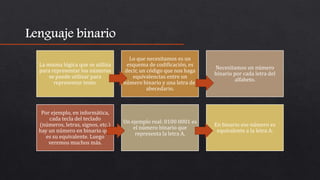
El documento explica los sistemas de numeración binario y decimal. El sistema binario representa números utilizando solo los dígitos 0 y 1 y es el sistema utilizado por computadoras debido a que estas funcionan con dos niveles de tensión eléctrica. También describe cómo se realizan operaciones aritméticas como la suma, resta, multiplicación y división en el sistema binario.

7. El sistema binario es un sistema de numeración en el que los
números se representan utilizando las cifras 0 y 1, es decir solo 2
dígitos (bi = dos).
Esto en informática y en electrónica tiene mucha importancia ya
que las computadoras trabajan internamente con 2 niveles: hay o
no hay de Tensión, hay o no hay corriente, pulsado o sin pulsar,
etc.
Esto provoca que su sistema de numeración natural sea el
binario, por ejemplo 1 para encendido y 0 para apagado.

14. Operamos como en el
sistema decimal:
comenzamos a sumar
desde la derecha, en
nuestro ejemplo, 1 + 1 =
10, entonces escribimos 0
en la fila del resultado y
nos llevamos 1 (este "1"
se llama arrastre).
A continuación se suman
los números de la
siguiente columna: 0 + 0
= 0, pero como nos
tenemos que sumar el 1
de la anterior suma, el
resultado será 0 + 1 = 1.

15. La resta 0 - 1 se resuelve,
igual que en el sistema
decimal, tomando una
unidad prestada de la
posición siguiente: 10 - 1
= 1 y me llevo 1, lo que
equivale a decir en
decimal, 2 - 1 = 1.
Esa unidad prestada debe
devolverse, sumándola, a
la posición siguiente.

16. Primero multiplicamos 101 por 1
, que produce 101. A
continuación, ponemos un 0
como un marcador de posición
al igual que como lo haría en la
multiplicación decimal y
multiplicamos 101 por 1 , que
produce 101.
101
x 1 1
101
101 0 <- el 0 aquí es el
marcador de posición
El siguiente paso, al igual que
con la multiplicación decimal, es
sumar.
101
x 11
101
1010
1111

17. 11 R = 10
11 ) 1011
-11
101
-11
10 <- resto, R
La división binaria es algo más complicada que la
multiplicación binaria. El proceso de división requiere
comprender bien como realizar las demás operaciones
aritméticas, por lo que te aconsejamos dominar la suma,
resta y multiplicación de binarios antes de aprender a
dividir números binarios.
Para realizar una división binaria , tenemos que seguir el
mismo proceso como lo hacemos para dividir números
decimales, pero, en este caso, sólo tenemos que decidir
si va a ser un 1 o un 0.
Para dividir dos números, básicamente hay que seguir
cuatro pasos: la división, multiplicación, resta y siguiente
dígito.
Para mostrar mejor como se debe realizar la division
binaria, a continuación vamos a dividir 1011 entre 11:

18. La misma lógica que se utiliza
para representar los números
se puede utilizar para
representar texto.
Lo que necesitamos es un
esquema de codificación, es
decir, un código que nos haga
equivalencias entre un
número binario y una letra del
abecedario.
Necesitamos un número
binario por cada letra del
alfabeto.
Por ejemplo, en informática,
cada tecla del teclado
(números, letras, signos, etc.)
hay un número en binario que
es su equivalente. Luego
veremos muchos más.
Un ejemplo real: 0100 0001 es
el número binario que
representa la letra A.
En binario ese número es
equivalente a la letra A.

19. El Código Estándar Americano para
el Intercambio de Información (ASCII)
fue desarrollado a partir de los
códigos telegráficos, pero luego fue
adaptado para representar texto en
código binario en los años 1960 y
1970.
La versión original de ASCII utiliza 8
bits (recuerda cada número binario
es un bit) para representar cada letra
o carácter, con un total de 128
caracteres diferentes.
Mientras ASCII se encuentra todavía en uso hoy
en día, el estándar actual para la codificación de
texto es Unicode.
El principio fundamental de Unicode es muy
parecido a ASCII, pero Unicode contiene más de
110.000 caracteres, cubriendo la mayor parte de
las lenguas impresas del mundo.
La relativamente simple versión de 8 bits de
Unicode (referido como UTF-8) es casi idéntica a
ASCII, pero las versiones de 16 y 32 bits (referido
como UTF-16 y UTF-32) le permiten representar
casi cualquier tipo de lenguaje impreso.

27. Octal Binario
1 00001
2 00010
3 00011
4 00100
5 00101
6 00110
7 00111
8 01000
9 01001
10 01010

28. 84 83 82 81 80
4096 512 64 8 1
7 0 2 1 5
Base elevada a la
posición
Dígitos Utilizados
+7*4096 +0*51
2
+2*64 +1*8 +5*1
+28672 0 +128 +8 +5
Multiplicamos la
posición elevada con
su respectivo digito
= 28813
 Primero, Elevaremos los dígitos con
sus posiciones correspondientes
empezando desde la izquierda.
 Segundo, multiplicaremos la posición
elevada con su respectivo digito.
 Tercero Dividiremos el resultado de la
suma de los que nos dio la
multiplicación.
 Cuarto el resultado de la división dará
como resultado el numero binario
28813/10
=111000 010001101

30. 83 82 81 80
512 64 8 1
3584 448 32 3

32. Tabla de Conversiones

35. Podemos llegar a la conclusión que los sistemas de numeración son muy usados en la actualidad, por
ejemplo habitualmente usamos el sistema decimal, y el binario esta presente en todos los sistemas
electrónicos digitales, es por ello que tenemos que tener una noción de lo mucho que significan hoy en
día.
A la hora de realizar las conversiones se puede observar que son un poco complicadas si no se tiene
conocimientos previo del tema, al realizar los ejercicios podemos darnos cuenta que no son tan sencillos
como lo aparentan ya que cada letra y/o número representan un valor absoluto.