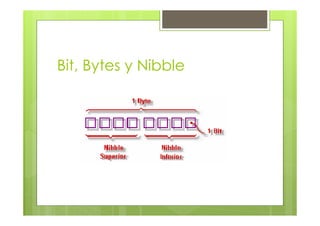
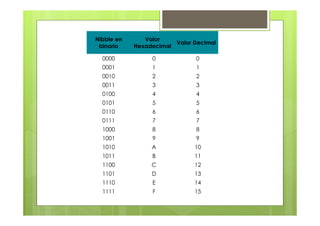
Este documento presenta información sobre un curso de informática, incluyendo el horario, temas, profesora y forma de aprobación. Los temas a cubrir incluyen sistemas de numeración binarios y decimales, conversión entre ellos, el tamaño de las cifras binarias, y la definición de conceptos como bit, byte y nibble.

1. Informática
Carrera: Bioingeniería –Ing.
Agroindustria
Profesora: Lic. S. Vanesa Torres

2. IMPORTANTE
Mail contacto:
informatica.unvime@gmail.com
Blog Materia

3. Horarios
Lunes
19 a 22 hsC1
Teórico/práctico

4. Régimen Aprobación
80% Asistencia
Materia Regularizar % - 1 examen escrito
práctico
Fecha examen 1/7

5. Temas
Sistema de Numeración
Conversión entre números decimales y
binarios.
El tamaño de las cifras binarias
Conversión entre números binarios a
decimal.
Bit, Bytes y Nibble.

6. Sistema de Numeración
El sistema binario, en ciencias e
informática, es un sistema de numeración
en el que los números se representan
utilizando solamente las cifras cero y uno
(0 y 1).
Es el que se utiliza en las computadoras,
debido a que trabajan internamente con
dos niveles de voltaje, por lo cual su
sistema de numeración natural es el
sistema binario (encendido 1, apagado
0).

7. Sistema de Numeración
En una cifra binaria, cada dígito tiene
distinto valor dependiendo de la posición
que ocupe.
El valor de cada posición es el de una
potencia de base 2, elevada a un
exponente igual a la posición del dígito
menos uno.
La base de la potencia coincide con la
cantidad de dígitos utilizados (2) para
representar los números.

8. Sistema de Numeración
De acuerdo con estas reglas, el número
binario 1011 tiene un valor que se calcula
así:
1*23 + 0*22 + 1*21 + 1*20 , es decir:
8 + 0 + 2 + 1 = 11
y para expresar que ambas cifras describen
la misma cantidad lo escribimos así:
10112 = 1110

9. Conversión entre números
decimales y binarios
Convertir un número decimal al sistema
binario es muy sencillo: basta con realizar
divisiones sucesivas por 2 y escribir los
restos obtenidos en cada división en
orden inverso al que han sido obtenidos.

10. Conversión entre números
decimales y binarios
Por ejemplo, para convertir al sistema binario
el número 7710 haremos una serie de divisiones
que arrojarán los restos siguientes:
77 : 2 = 38 Resto: 1
38 : 2 = 19 Resto: 0
19 : 2 = 9 Resto: 1
9 : 2 = 4 Resto: 1
4 : 2 = 2 Resto: 0
2 : 2 = 1 Resto: 0
1 : 2 = 0 Resto: 1

11. Conversión entre números
decimales y binarios
y, tomando los restos en orden inverso
obtenemos la cifra binaria:
7710 = 10011012

12. Conversión entre números
decimales y binarios
A modo de ejemplo realizar:
191
25
67
99
135
276

13. El tamaño de las cifras
binarias
La cantidad de dígitos necesarios para
representar un número en el sistema
binario es mayor que en el sistema
decimal. En el ejemplo del párrafo
anterior, para representar el número 77,
que en el sistema decimal está
compuesto tan sólo por dos dígitos, han
hecho falta siete dígitos en binario.

14. El tamaño de las cifras
binarias
Para representar números grandes harán
falta muchos más dígitos. Por ejemplo,
para representar números mayores de
255 se necesitarán más de ocho dígitos,
porque 28 = 256 y podemos afirmar, por
tanto, que 255 es el número más grande
que puede representarse con ocho
dígitos.

15. El tamaño de las cifras
binarias
Como regla general, con n dígitos binarios
pueden representarse un máximo de 2n,
números. El número más grande que puede
escribirse con n dígitos es una unidad menos, es
decir, 2n – 1. Con cuatro bits, por ejemplo,
pueden representarse un total de 16 números,
porque 24 = 16 y el mayor de dichos números es
el 15, porque 24-1 = 15.

16. El tamaño de las cifras
binarias
Ejercicio 1:
Averigua cuántos números pueden
representarse con 8, 10, 16 y 32 bits y cuál es
el número más grande que puede escribirse
en cada caso.
Ejercicio 2:
Dados dos números binarios: 01001000 y
01000100 ¿Cuál de ellos es el mayor?

17. Conversión de binario a
decimal
El proceso para convertir un número del
sistema binario al decimal es aún más
sencillo; basta con desarrollar el número,
teniendo en cuenta el valor de cada
dígito en su posición, que es el de una
potencia de 2, cuyo exponente es 0 en el
bit situado más a la derecha, y se
incrementa en una unidad según vamos
avanzando posiciones hacia la izquierda.

18. Conversión de binario a
decimal
Por ejemplo, para convertir el número
binario 10100112 a decimal, lo
desarrollamos teniendo en cuenta el
valor de cada bit:
1*26 + 0*25 + 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 83
10100112 = 8310

19. Conversión de binario a
decimal
Expresa, en el sistema decimal, los
siguientes números binarios:
110111
111000
010101
101010
1111110

20. Bit, Bytes y Nibble
BIT. El ordenador se compone de dispositivos
electrónicos digitales, por lo tanto éstos solo
pueden adoptar únicamente dos estados,
que representamos matemáticamente por 0
y 1.
Cualquiera de estas unidades de información
se denomina BIT, contracción de «binary
digit» en inglés.

21. Bit, Bytes y Nibble
BYTE. Cada grupo de 8 bits se conoce
como byte u octeto. Es la unidad de
almacenamiento en memoria, la cual está
constituida por un elevado número de
posiciones que almacenan bytes.
La cantidad de memoria de que dispone
un sistema se mide en Kilobytes (1 Kb =
1024 bytes), en Megabytes (1 Mb = 1024
Kb), Gigabytes (1 Gb = 1024 Mb), Terabytes
(1 Tb = 1024 Gb) o Petabytes (1 Pb = 1024
Tb).

22. Bit, Bytes y nibble
NIBBLE. Cada grupo de cuatro bits de un
byte constituye un nibble, de forma que
los dos nibbles de un byte se llaman
nibble superior (el compuesto por los bits
4 a 7) e inferior (el compuesto por los bits
0 a 3).

23. Bit, Bytes y Nibble

24. Sistema Hexadecimal
Es un sistema posicional de numeración
en el que su base es 16, por tanto,
utilizara 16 símbolos para la
representación de cantidades. Estos
símbolos son:
0 1 2 3 4 5 6 7 8 9 A B C D E F
Es uno de los sistemas más utilizados en
electrónica, ya que además de
simplificar la escritura de los números
binarios, todos los números del sistema se
pueden expresar en cuatro bits binarios al
ser 16 = 24

25. Significado de Nibble
Un bit es la posición que ocupa un número el cual
será "0" o "1" ya que son los únicos valores que
admite.
Si dispones de un bit solo tienes 2 posibilidades.
1ra. Posibilidad - 1
2da. Posibilidad - 0
Si dispones de 2 bits tienes 4 posibles
combinaciones.
1ra. Combinación – 00
2da. Combinación - 01
3ra. Combinación - 10
4ta. Combinación - 11

26. Significado de Nibble
En fin si dispones de 4 bit tienes 16 posibles
combinaciones que son:
Pues bien, estas son las que corresponden a un
NIBBLE, esto es muy importante ya que cada
nibble representa una cifra en el sistema
hexadecimal que van desde el 0 al 9 y luego de
la A a la F.
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

27. Nibble en
binario
Valor
Hexadecimal
Valor Decimal
0000 0 0
0001 1 1
0010 2 2
0011 3 3
0100 4 4
0101 5 5
0110 6 6
0111 7 7
1000 8 8
1001 9 9
1010 A 10
1011 B 11
1100 C 12
1101 D 13
1110 E 14
1111 F 15

28. Nibble
El sistema de numeración hexadecimal
agrupa los bits de a cuatro, es por eso
que aparecen los nibbles (grupos de 4
bits), observa esta equivalencia de
ejemplo; y verifica que sea verdad de
acuerdo...
Byte Valor hexadecimal
0111 0101 75