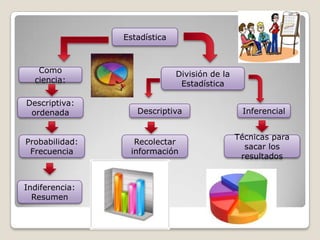
El documento presenta conceptos básicos de estadística. Define población, muestra, muestra aleatoria y variables. Explica que una población es el conjunto total de personas u objetos sobre los cuales se recopilan datos, mientras que una muestra es una parte de la población que representa a toda la población. También describe diferentes tipos de técnicas de muestreo como el muestreo aleatorio, estratificado y sistemático.

1. INSTITUTO UNIVERSITARIO DE TECNOLOGIA
“ANTONIO JOSE DE SUCRE”
EXTENSION BARQUISIMETO
Estadística
Autor:
Leonel Ocanto
Barquisimeto, Abril de 2013

2. C
O
N
C
E
P
T
O
S
B
A
S
I
C
O
S
Población
Suma de personas que conviven
dentro de un pueblo, provincia,
país, u otra área geográfica, y
poseen comúnmente,
características en común. También
se dice “población” a la acción o
acto de poblar. Ejemplo: niños.
Muestra
"Se llama muestra a una parte de
la población a estudiar que sirve
para representarla". Murria R.
Spiegel (1991). Ejemplo:
estudiamos los valores sociales
de una población de 5000
habitantes aprox.
Muestra Aleatoria
Una selección que se escoge
aleatoriamente (puramente por
azar, impredeciblemente).
Ejemplo: si tu quisieras tomar una
muestra aleatoria de agua de un
río, podrías tomar un mapa del río
y escoger un punto con los ojos
vendados ¡y a ver entonces cómo
llegas allí!

3. C
O
N
C
E
P
T
O
S
B
A
S
I
C
O
S
Parámetro
el establecimiento de un condicional
que puede alterar tanto el
comportamiento como la estadística
de un término predeterminado,
modificando el valor que pueda llegar
adquirir o las distintas condiciones
que rodean al mismo.
Estadistico
Dada una población X y una muestra de tamaño
n, es decir, una sucesión de variables aleatorias,
X1,X2,...,Xn , réplicas de X; se entiende por
estadístico cualquier variable aleatoria,
E(X1,X2,...,Xn) (o simplemente E) , que se defina
a partir de las n variables que integran dicha
muestra. La realización de la muestra, lo cual
supone extracción de la población y evaluación de
X en cada uno de los n individuos, aporta n datos
u observaciones x1,x2,...,xn ; que, reemplazados
en la expresión del estadístico, establece el valor
de éste para la muestra en particular.
Variable
Elemento que puede tomar
cualquier valor de los
comprendidos en un
conjunto. Ejemplo: un ser
humano.

4. C
O
N
C
E
P
T
O
S
B
A
S
I
C
O
S
Datos
Son los hechos que describen
sucesos y entidades. Ejemplo:
letras del alfabeto, números,
movimientos de labios, puntos
y rayas, señales con la mano,
dibujos.
Censo
Recuento de individuos que
conforman una población
estadística, definida como un
conjunto de elementos de
referencia sobre el que se
realizan las observaciones
Encuesta
Es un estudio observacional en el
cual el investigador busca
recaudar datos por medio de un
cuestionario prediseñado, y no
modifica el entorno ni controla el
proceso que está en observación.

5. Estadística
Probabilidad:
Frecuencia
Descriptiva:
ordenada Inferencial
División de la
Estadística
Como
ciencia:
Indiferencia:
Resumen
Técnicas para
sacar los
resultados
Descriptiva
Recolectar
información

6. De la lámina 9, exponer su interpretación, esto en una
(1) lámina.
Por análisis se entiende la separación de las partes de un
todo hasta llegar a conocer sus principios o elementos.
Si extendemos esta definición al ámbito estadístico,
podremos afirmar que el análisis estadístico es el
análisis que emplea técnicas estadísticas para
interpretar datos, ya sea para ayudar en la toma de
decisiones o para explicar los condicionantes que
determinan la ocurrencia de algún fenómeno. Allí se
explica el conjunto de factores que intervienen en los
procesos estadísticos.

7. Pasos en un estudio estadístico
• Plantear hipótesis sobre una población.
• Qué individuos pertenecerán al estudio Buscar las
muestras.
• Criterios de exclusión ¿Cómo se eligen? ¿Descartamos
los que padecen enfermedades crónicas?
• Qué datos recoger de los mismos (variables).
• Recoger los datos (muestreo) ¿Estratificado?
¿Sistemáticamente?
• Describir (resumir) los datos obtenidos:
• Realizar una inferencia sobre la población.
• Cuantificar

8. T
E
C
N
I
C
A
S
D
E
M
U
E
S
T
R
E
O
Muestreo Aleatorio:
En un salón hay 20 niñas, se quiere
extraer una muestra y se escogen 5
niñas sin beneficiar a ninguna.
Muestreo Estratificado:
Para un estudio de opinión, puede resultar interesante
estudiar por separado las opiniones de hombres y
mujeres pues se estima que, dentro de cada uno de
estos grupos, puede haber cierta homogeneidad. Así,
si la población está compuesta de un 55% de mujeres
y un 45% de hombres, se tomaría una muestra que
contenga también esa misma proporción.
Muestreo por conglomerado:
Se planea hacer una encuesta entre universitarios de
primer curso de un país. Se quieren entrevistar 5.000
universitarios. Ante la imposibilidad de acceder (de
acuerdo con los costos) a un muestreo estratificado,
se piensa en una muestra de 200 conglomerados de
25 alumnos, identificando el conglomerado con un
grupo de primer curso.
Muestreo sistemático:
si tenemos una población de 100 individuos y queremos seleccionar una
muestra de 20, actuaríamos de la siguiente forma:
Numeramos los elementos o personas.
Tenemos que elegir un elemento de cada 100/20= 5 (coeficiente de
elevación).
Elegimos al azar un elemento o persona entre los 5 primeros.
Supongamos que elegimos el número 2.
Posteriormente seleccionamos un elemento cada 5, es decir, el 2+5=7,
7+5=12, etc. El último sería el elemento número 97.

9. Tipos de Variables
Cuantitativas: estas variables se expresan por medio de un
número, lo que permite utilizarlas para operaciones aritméticas.
Dentro de estas encontramos dos clases:
• Continua: este tipo de variables puede adquirir valores
existentes entre dos números.
• Discreta: esta variable no puede adquirir valores intermedios
entre dos números, sino aislados.
Cualitativas: hace alusión a aquellas cualidades que no se las
puede medir numéricamente. Dentro de estas variables
encontramos dos clases:
• Variable cualitativa ordinal o cuasicuantitativa: este tipo de
variables presentan modalidades no numéricas en las que hay
un orden.
• Variable cualitativa ordinal: en este tipo de variables, en
cambio, las modalidades numéricas no pueden ser ordenadas
bajo ningún criterio.

10. En variables que exploran el grado de acuerdo o desacuerdo frente a una
afirmación los atributos podrían ser:
 1 = muy en desacuerdo
 2 = en desacuerdo
 3 = indiferente
 4 = de acuerdo
 5 = muy de acuerdo
Dependiendo de los valores que puede tener una variable cualitativa, ésta
puede a su vez ser dicotómicas (cuando sólo pueden adoptar un sólo valor sin
jerarquía entre sí; hombre - mujer, positivo-negativo, presente-ausente), o
bien, poli o multicotómicas, si existe la posibilidad de que adopten múltiples
valores (edad, talla, nivel socioeconómico, grupos sanguíneos, calificación
previsional de usuarios).

11. Frecuencia absoluta
La frecuencia absoluta es el número de veces que
aparece un determinado valor en un estudio
estadístico.
Se representa por fi.
La suma de las frecuencias absolutas es igual al
número total de datos, que se representa por N.
Para indicar resumidamente estas sumas se utiliza la
letra griega Σ (sigma mayúscula) que se lee suma o
sumatoria.

12. Frecuencia Relativa
La frecuencia relativa es el cociente
entre la frecuencia absoluta de un
determinado valor y el número total de
datos.
Se puede expresar en tantos por ciento
y se representa por ni.
La suma de las frecuencias relativas es
igual a 1.

13. Frecuencia acumulada
La frecuencia acumulada es la
suma de las frecuencias
absolutas de todos los valores
inferiores o iguales al valor
considerado.
Se representa por Fi.