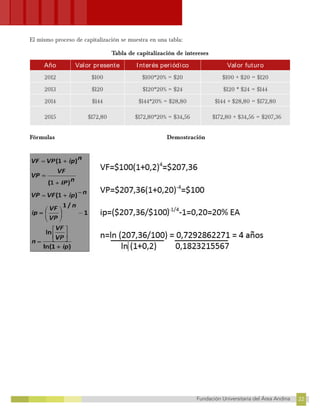
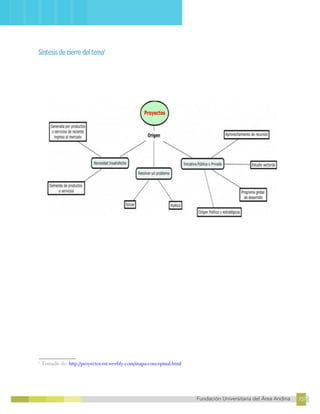
Este documento trata sobre las matemáticas financieras y contiene cuatro unidades temáticas. La primera unidad explica los tipos de interés simple y compuesto. La segunda unidad habla sobre el valor del dinero en el tiempo y los flujos de efectivo. La tercera unidad cubre los temas de anualidades y amortizaciones. La cuarta y última unidad trata sobre títulos de valor y la evaluación de proyectos. El documento provee los conceptos teóricos y metodología para cada unidad con el fin de calcular operaciones financieras