Incrustar presentación
Descargar para leer sin conexión

![Longitud de una curva
La idea para calcular la longitud de una curva contenida en el plano o en el espacio consiste en
dividirla en segmentos pequeños, escogiendo una familia finita de puntos en C, y aproximar la
longitud mediante la longitud de la poligonal que pasa por dichos puntos. Cuantos más puntos
escojamos en C, mejor será el valor obtenido como aproximación de la longitud de C.
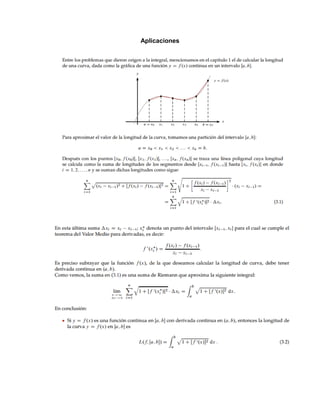
Para ello, escogemos una parametrizacion α : *a, b+ −→ R n de C, y una partición P = ,a = t0 ≤ t1 ≤
t2 ≤ · · · ≤ tk = b-, y calculamos aproximadamente la longitud del arco α(*ti , ti+1+) como la longitud
del segmento *α(ti), α(ti+1)+. Utilizando la norma Euclides en R n , y aplicando a las coordenadas de
α el teorema del valor medio en el intervalo *ti , ti+1].](https://image.slidesharecdn.com/longituddecurvas-200331235757/85/Longitud-de-curvas-2-320.jpg)


El documento describe cómo calcular la longitud de una curva dividiéndola en segmentos pequeños y aproximando la longitud total como la suma de las longitudes de los segmentos individuales. Se elige una partición de puntos en la curva y se calcula la longitud aproximada del arco entre puntos consecutivos como la longitud del segmento que los une. Cuanto más fina sea la partición, mejor será la aproximación.

![Longitud de una curva
La idea para calcular la longitud de una curva contenida en el plano o en el espacio consiste en
dividirla en segmentos pequeños, escogiendo una familia finita de puntos en C, y aproximar la
longitud mediante la longitud de la poligonal que pasa por dichos puntos. Cuantos más puntos
escojamos en C, mejor será el valor obtenido como aproximación de la longitud de C.
Para ello, escogemos una parametrizacion α : *a, b+ −→ R n de C, y una partición P = ,a = t0 ≤ t1 ≤
t2 ≤ · · · ≤ tk = b-, y calculamos aproximadamente la longitud del arco α(*ti , ti+1+) como la longitud
del segmento *α(ti), α(ti+1)+. Utilizando la norma Euclides en R n , y aplicando a las coordenadas de
α el teorema del valor medio en el intervalo *ti , ti+1].](https://image.slidesharecdn.com/longituddecurvas-200331235757/85/Longitud-de-curvas-2-320.jpg)


