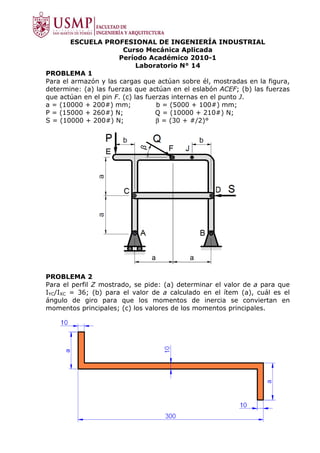
Este documento presenta 3 problemas de mecánica aplicada relacionados con estructuras y momentos de inercia. El Problema 1 pide determinar las fuerzas que actúan en diferentes partes de una estructura dada sus dimensiones y cargas aplicadas. El Problema 2 solicita calcular el valor de una dimensión y el ángulo de giro necesario para que los momentos de inercia se conviertan en principales para un perfil dado. El Problema 3 requiere hallar la dimensión de una zeta, el ángulo de orientación de sus ejes

1. ESCUELA PROFESIONAL DE INGENIERÍA INDUSTRIAL
Curso Mecánica Aplicada
Período Académico 2010-1
Laboratorio N° 14
PROBLEMA 1
Para el armazón y las cargas que actúan sobre él, mostradas en la figura,
determine: (a) las fuerzas que actúan en el eslabón ACEF; (b) las fuerzas
que actúan en el pin F. (c) las fuerzas internas en el punto J.
a = (10000 + 200#) mm; b = (5000 + 100#) mm;
P = (15000 + 260#) N; Q = (10000 + 210#) N;
S = (10000 + 200#) N; β = (30 + #/2)°
PROBLEMA 2
Para el perfil Z mostrado, se pide: (a) determinar el valor de a para que
IYC/IXC = 36; (b) para el valor de a calculado en el ítem (a), cuál es el
ángulo de giro para que los momentos de inercia se conviertan en
momentos principales; (c) los valores de los momentos principales.

2. PROBLEMA 3
Una zeta fabricada de plancha de 3/8” de espesor se une a un ángulo L 5”
x 3” x 1/2” como se muestra en la figura. Si se sabe que el centroide C de
la sección combinada se localiza sobre el eje centroidal y, como se
muestra en la figura y que b = (4 +#/5) pulgadas, determine: (a) la
dimensión a de la zeta; (b) el ángulo θm que determina la orientación de
los ejes principales; (c) los momentos de inercia máximo y mínimo con
respecto a los ejes principales que pasan por el centroide C de la sección
combinada.
Ing. Alejandro Orlando Huapaya Bautista
Profesor de la parte práctica del curso
Junio de 2010