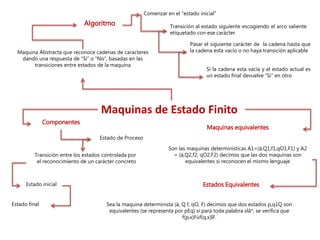
Este documento describe las máquinas de estado finito, que son máquinas abstractas que reconocen cadenas de caracteres y devuelven una respuesta de "sí" o "no" basada en las transiciones entre estados. Comienzan en un estado inicial, pasan al estado siguiente según el carácter actual, y continúan hasta que la cadena esté vacía o no haya más transiciones, devolviendo "sí" si terminan en un estado final.

1. Universidad Fermín Toro
Maquinas de Estado Finito
María Aponte
Estructuras Discretas II
Cabudare 2016

2. Maquina Abstracta que reconoce cadenas de caracteres
dando una respuesta de “Si” o “No”, basadas en las
transiciones entre estados de la maquina
Algoritmo
Comenzar en el “estado inicial”
Transición al estado siguiente escogiendo el arco saliente
etiquetado con ese carácter
Pasar el siguiente carácter de la cadena hasta que
la cadena esta vacío o no haya transición aplicable
Si la cadena esta vacía y el estado actual es
un estado final devuelve “Si” en otro
Componentes
Estado de Proceso
Transición entre los estados controlada por
el reconocimiento de un carácter concreto
Estado inicial
Estado final
Maquinas equivalentes
Son las maquinas determinísticas A1=(ä,Q1,f1,qO1,F1) y A2
= (ä,Q2,f2, qO2,F2) decimos que las dos maquinas son
equivalentes si reconocen el mismo lenguaje
Estados Equivalentes
Sea la maquina determinista (ä, Q f, qO, F) decimos que dos estados p,q1Q son
equivalentes (se representa por pEq) si para toda palabra xlä*, se verifica que
f(p,x)Füf(q,x)IF.
Maquinas de Estado Finito