Matematica Ingreso 2009

Facultad de Agronomía y Veterinaria

INTRODUCCIÓN
Todo alumno interesado en las Ciencias Agropecuarias muestra afinidad con asignaturas
relacionadas con biología, fisiología, morfología, anatomía, patología, maquinarias
agrícolas, producción vegetal o animal. Sin embargo, al comienzo de esta nueva etapa de
formación y crecimiento, la pregunta más frecuente es Matemática, ¿Por qué?, ¿Para
qué? si yo quiero estudiar Medicina Veterinaria o Ingeniería Agronómica.
El objetivo de este material es satisfacer esta inquietud pensando en que la transmisión de
los conocimientos básicos de la asignatura debe hacerse a través de situaciones aplicadas
y contextualizadas a las Ciencias Agropecuarias aumentando el interés y la motivación
para así de esta manera comprender la necesidad de adquirir dichos conocimientos.
En este material, cada concepto matemático es explicado y ejemplificado a través de
situaciones contextualizadas que introduce al alumno en problemas que encontrará a lo
largo de su vida académica y profesional.
Esto se ha logrado por la experiencia adquirida en estos últimos años participando en
proyectos de articulación curricular con el Nivel Medio e interactuando con docentes de
distintas asignaturas de la Facultad de Agronomía y Veterinaria donde se utiliza la
matemática como una herramienta fundamental.
Pretendemos que este módulo sirva como una guía de estudios que permita reflexionar,
analizar, discutir resultados e incorporar conceptos sin reemplazar los libros de texto.

2


ÍNDICE ANALÍTICO
INTRODUCCIÓN 2

CAPITULO I: NÚMEROS
1.1- Números Naturales: Propiedades. 5
1.2- Números Enteros: Propiedades. 5
1.3- Números Racionales: Propiedades. 6
1.4- Números Irracionales: Definición. 7
1.5- Números Reales: Propiedades. 8
1.6- Operaciones en R: Multiplicación, Regla de los Signos, Propiedades;
Potenciación, Potencia de Exponente Natural, Potencia de
8
Exponente Negativo, Propiedades; Radicación,
Propiedades.
1.7- Notación Científica. 14
1.8- Ejercicios de Aplicación. 14

CAPITULO II: RAZÓN Y PROPORCIÓN NUMERICA
2.1- Razón Entre dos Números. 17
2.2- Proporción Numérica. 17
2.3- Magnitudes Directamente Proporcionales. 17
2.4- Regla de Tres Simple Directa. 18
2.5- Porcentaje. 20

CAPITULO III: ECUACIONES
3.1- El Misterio de las Ecuaciones. 23
3.2- Definición. 23
3.3- Resolución de Ecuaciones. 24
3.4- Tipos de Ecuaciones. 26
3.5- Sistema de Ecuaciones. 27
3.6- Resolución de Ecuaciones Racionales. 28

CAPITULO IV: UNIDADES
4.1- Sistema de Unidades. 34
4.2- El Patrón de Longitud. 35
4.3- El Patrón de Masa. 35
4.4- El Patrón de Tiempo. 35
4.5- Introducción al Análisis Dimensional. 37
4.6- Cambios de Unidades. 38

3


CAPITULO V: FUNCIONES
5.1- Introducción. 43
5.2- Funciones: Definición. 44
5.3- Funciones Numéricas: Definición. 45
5.4- Representación Grafica de Funciones. 47
5.5- Clasificación para Funciones Reales: Funciones Crecientes y Decrecientes;
49
Funciones Pares e Impares.
5.6- Función Lineal. 50
5.7- Función Cuadrática. 53

BIBLIOGRAFÌA 62

4


CAPITULO I: NÚMEROS

1.1- NÚMEROS NATURALES
Fue el primer conjunto numérico que se conoció y se lo utilizó fundamentalmente para
contar. Se lo identifica con N

N = {0, 1, 2, 3, 4,........... }

PROPIEDADES

1.- N es un conjunto formado por infinitos elementos
2.- N es un conjunto totalmente ordenado. Es decir, dados dos números naturales, se puede
establecer exactamente cual es el mayor y cual es el menor. O sea, si a y b son números
naturales distintos, entonces:

a<b o b<a

3.- N tiene primer elemento, pero no tiene último elemento. Cualquiera sea el número
natural que se elija, siempre es posible hallar su siguiente; basta con sumar uno al número
elegido. Pero no siempre es posible hallar su anterior; el cero, por ejemplo, tiene siguiente
pero no tiene anterior. Por eso el cero es el primer elemento del conjunto.
4.- N es en conjunto discreto. Es decir, entre dos números naturales hay un número finito
de números naturales.
5.- La suma de dos números naturales es un número natural.
6.- El producto de dos números naturales es un número natural.

1.2- NÚMEROS ENTEROS

El conjunto N no basta para resolver todos los problemas que se plantean a diario ¿Cómo
haríamos para resolver la ecuación: x + 6 = 2? Para ello se crearon los números enteros y se
los identifica con Z
Z = {......., -3, -2, -1, 0, 1, 2, 3,......}

PROPIEDADES

1.- Z es un conjunto formado por infinitos elementos.
2.- Z es un conjunto totalmente ordenado.
3.- Z no tiene primer elemento ni último elemento. Es decir, todo número entero tiene su
anterior y su siguiente.
4.- Z es un conjunto discreto.
5.- La suma de dos números enteros, es un número entero.
6.- El producto de dos números enteros, es un número entero.
7.- Todo número entero a tiene su opuesto b, tal que:
a+b=b+a=0

5


1.3- NÚMEROS RACIONALES

Los números fraccionarios se inventaron como respuesta a la necesidad de expresar partes
de la unidad, en especial, cuando se realizaban mediciones. Por este motivo, tuvieron un
desarrollo apreciablemente anterior al de los números enteros.
Los enteros y las fracciones positivas y negativas forman el conjunto de los números
racionales. Este conjunto se indica por Q.
Los números racionales se pueden escribir como fracción o como expresiones decimales.
Por ej:

3 271
se puede escribir como 0,6 2,71 se puede escribir como
5 100

Dentro de las expresiones decimales, podemos encontrar las exactas y las periódicas. Por
ej:

3
= 0,75 (expresión decimal exacta)
4

2 )
= 0,13 (expresión decimal periódica)
15

En las expresiones decimales periódicas, hay infinitas cifras decimales a la derecha de la
coma, que aparecen con determinada periodicidad (estas cifras se indican dibujándolas
debajo de un arco).
Resumiendo:
Los números racionales son aquellos que se pueden expresar como el cociente o razón de
dos números enteros. De allí su nombre. La única condición es que el denominador sea
distinto de cero.

PROPIEDADES

1.- Q es un conjunto formado por infinitos elementos.
2.- Q es un conjunto totalmente ordenado.
3.- Q no tiene primer elemento ni último elemento.
4.- Entre dos números racionales existen infinitos racionales. Por eso se dice que es un
conjunto denso. Como consecuencia de esto, no tiene sentido hablar del anterior y del
posterior de un número racional.

6


SIMPLIFIQUEMOS NÚMERO RACIONALES

Simplificar una fracción es sustituirla por otra equivalente con los términos más sencillos.
Esto lo podés hacer cuando numerador y denominador se pueden dividir por un mismo
número:
3 1 15 5 180 3
= ; = ; =
60 20 12 4 120 2

Para que te resulte más fácil es conveniente que simplifiques dos fracciones en varios
pasos:
180 18 9
= = =
120 12 6

Cuando una fracción no se puede simplificar más, se dice que es irreducible.

Son fracciones irreducibles, por ejemplo:
5 1 3 17 16
; ; ; ;
4 20 2 20 15

Para ordenar números enteros o por ejemplo números decimales se usa la recta numérica.
Si querés comparar dos expresiones decimales, es necesario que las mismas tengan la
misma cantidad de números después de la coma. Para comparar 0,5 y 0,04.
Como 0,5 = 0,50 entonces comparo 0,50 > 0,04 y luego contesto 0,5 > 0,04.

Si quiero comparar 9,12 y 9,135 entonces:
9,12 = 9,120 luego comparo 9,120 < 9,135 y contesto:
9,12 < 9,135
Si quiero comparar 0,00135 y 0,005 entonces:
0,005 = 0,00500 luego comparo 0,00135 < 0,00500 y contesto:
0,00135 < 0,005

1.4- NÚMEROS IRRACIONALES

Los números irracionales son aquellos que no pueden escribirse como el cociente o razón
de dos números enteros. Se caracterizan porque a la derecha de la coma decimal, poseen
infinitas cifras decimales no periódicas. A este conjunto se lo indica por I. Son números
irracionales las raíces de números naturales que no son enteras, π (la relación entre el
perímetro y el diámetro de una circunferencia), el número e (la base de los logaritmos
naturales), la raíz cuadrada de 2, etc.

7


1.5- NÚMEROS REALES

Es el conjunto formado por los números racionales e irracionales. A este conjunto se lo
indica por “R”.

N
Naturales
Z
Enteros
Naturales Q
Negativos Racionales

Números R
Fraccionarios Reales

I
Irracionales

PROPIEDADES

1.- R es un conjunto formado por infinitos elementos
2.- R no tiene primer ni último elemento
3.- R es un conjunto denso
4.- R es un conjunto totalmente ordenado

1.6- OPERACIONES EN “R”`

MULTIPLICACION
a.b = a + a 4a +4244443
14 + 4 4+ ............... 4a
a +
b veces
Los números a y b se denominan factores, y el resultado, producto. Por ej:

3.4 = 3 +4 + 3 + 3
1 324 3
4 veces

5.2 = 5 + 5
{
2 veces

8


REGLA DE LOS SIGNOS

si se multiplican dos factores positivos o dos factores negativos, el producto es positivo
si se multiplican dos factores de signos distintos, el producto es negativo

PROPIEDADES
1.- Conmutativa:
a.b = b.a

Por ej:

3.4 = 4.3 = 12

2.- La multiplicación es distributiva respecto de la suma y la resta:

a.(b + c) = a.b + a.c

a.(b – c) = a.b – a.c

Por ej:
3.(4 + 5) = 3.4 + 3.5
3.9 = 12 + 15
27 = 27

4.(5 – 3) = 4.5 – 4.3
4.2 = 20 –12
8=8

POTENCIACIÓN
a n = a .a. a44 444. a
14 . a ................3
2
n veces
Al número a se lo denomina base y al número n, exponente. Al resultado, se lo denomina
potencia.

Por ej:
2 3 = 2.2.2
{ 5 2 = 5.5
{
3 veces 2 veces

POTENCIA DE EXPONENTE NATURAL
si el exponente es un número par, la potencia es positiva
si el exponente es un número impar, la potencia lleva el signo de la base

9


Por ej:
32 = 9 33 = 27
(-5)2 = 25 (-2)3 = -8

POTENCIA DE EXPONENTE NEGATIVO
−n n
⎛a⎞ ⎛b⎞ bn
⎜ ⎟ =⎜ ⎟ = n
⎝b⎠ ⎝a⎠ a

Por ej:
−2 2
⎛3⎞ ⎛4⎞ 4 2 16
⎜ ⎟ =⎜ ⎟ = 2 =
⎝4⎠ ⎝3⎠ 3 9

PROPIEDADES

1.- La potencia primera de un número es ese mismo número

a1 =a

Por ej:
51 = 5 , 71 = 7

2.- La potencia cero de cualquier número (distinto de cero), es igual a uno

a0 = 1 (a≠ 0)
Por ej:
50 = 1 (-7)0 = 1

3.- La potencia no es distributiva respecto de la suma y la resta

(a + b)n ≠ an + bn
(a – b) n ≠ an – bn
Por ej:
(3 + 5 )2 ≠ 32 + 52
82 ≠ 9 + 25
64 ≠ 34

(3 - 5 )2 ≠ 32 - 52
(-2)2 ≠ 9 - 25
4 ≠ -16

10


4.- La potencia es distributiva respecto de la multiplicación y la división:
(a.b)n = an.bn
(a:b)n = an:bn
Por ej:
(3.4)2 = 32.42
122 = 9.16
144 = 144

(6:3)2 = 62:32
22 = 36:9
4=4

5.- El producto de dos o más potencias de igual base es otra potencia de la misma base
donde el exponente resulta de la suma de los exponentes de los factores
ax.ay = a(x+y)
Por ej:
23.24 = 2(3+4) = 27

6.- El cociente de dos potencias de igual base es otra potencia de la misma base donde el
exponente resulta de la resta de los exponentes del dividendo y del divisor
ax:ay = a(x-y)
Por ej:
25:22 = 2(5-2) = 23

7.- Potencia de otra potencia. El resultado es otra potencia de la misma base donde el
exponente resulta de la multiplicación de los exponentes
(ax)y = a x.y
Por ej:
(22)3 = 2 2..3 = 26

11


RADICACIÓN
n
a =r
La expresión anterior se lee “la raíz enésima de a es r”, donde n se llama índice, a
radicando y r raíz. El símbolo se llama radical.
Aquí se deben diferenciar los casos en que n es par o impar:

Para n par y a ≥ 0:
n a = r ⇒rn = a

Para n impar:
n a = r ⇒rn = a

Por ej:
29 =3
38 =2

3
−8 =−2

PROPIEDADES

1.- La radicación no es distributiva respecto de la suma y la resta:

n a +b = n a + n b
/

n a−b = n a −n b
/
Por ej:
9 + 16 = 9 + 16
/ 100 − 36 = 100 − 36
/
25 = 3 + 4
/ 64 = 10 − 6
/
5=7
/ 8=4
/

2.- La radicación es distributiva respecto de la multiplicación y la división
n a⋅b = n a ⋅n b

n a ÷b = n a ÷n b

12


Por ej:

4⋅9 = 4 ⋅ 9 100 ÷ 25 = 100 ÷ 25
36 = 2 ⋅ 3 4 = 10 ÷ 5
6=6 2=2

3.- Raíces sucesivas

nm
x = n ⋅m x
Por ej:
32
64 = 3⋅2 64
3
8 = 6 64
2=2

4.- Raíz de exponente racional
m
n
xm = x n

Por ej:
3
2
43 = 4 2

5.- Simplificación de radicales:
n
si n es impar:
n
xn = x n =x

Por ej:
3
3
− 2 3 = (− 2 ) 3 = −2

si n es par:
n
xn = x

Por ej:
− 32 = − 3 = 3

13


1.7- NOTACIÓN CIENTIFICA

La notación científica es una forma de expresar números que resulta muy conveniente
cuando se necesita manipular números muy grandes o muy pequeños. Consiste en expresar
al número como un producto entre un número decimal, cuyo valor absoluto sea mayor o
igual a uno y menor que diez, y una potencia de diez. Por ej:
700 = 7.102 0,0005 = 5.10-4
3
5600 = 5,6.10 0,0921 = 9,21.10-2
¿Qué es la notación científica?
Para definir con total claridad lo que esto significa consideremos el siguiente ejemplo:
La población de cierto microorganismo en un determinado medio de cultivo es de
6.000.000.000.
Veamos si encontramos una forma más abreviada para expresar este valor.
Si te fijás, verás que 6.000.000.000 es lo mismo que multiplicar 6 por 1.000.000.000,
entonces,
6.000.000.000 = 6 1.000.000.000 = 6 10 10 10 10 10 10 10 10 10 = 6 109 este
resultado se lee: “seis por diez a la nueve”

Otro ejemplo sería:
¿Sabías que el tiempo que tarda la luz en atravesar el vidrio de una ventana es de
0,000000000013 segundos?
13 13 -12
0,000000000013 = = 12
= 13 . 10 = 1,3 .10. 10-12 = 1,3 . 10-11
1000000000 000 10
A esta manera de escribir los números se la llama notación científica.

Un número está expresado en notación científica cuando se lo escribe de forma: p . 10 k,
donde p es un número decimal, cuyo valor absoluto es mayor o igual que 1 y menor que 10,
y k es un número entero.

1.8- EJERCICIOS DE APLICACIÓN

Ejercicio N°1: Aplicando las propiedades correspondientes, halla:

3
a) 729 = e)
4
46 =
35
b) x 30 = f)
16
=
81
c)
5
−16 ⋅ 5 2 = g) 12 ⋅ 3 =

5 3 11 1
d) 3 − = h) − =
8 4 4 2

14


Ejercicio N°2: Expresa el radical que corresponda:

1 2
a) 8 2 = b) 5 3 =
3
⎛ 1⎞ 2 1
c) ⎜ − ⎟ = d) 49 2 =
⎝ 4⎠
3 3
e) 2 4 = f) 4 5 =

Ejercicio N°3: Expresa como potencia

5
a) 72 = b) x 4 =
3
c) 7= d) 3 5 =
e) x9 = f) 3
− 125 =

Ejercicio N°4: Calcular las siguientes potencias
−1
⎛ 4⎞ 2 1
a) ⎜ ⎟ = b) (121)− 2 =
⎝ 25 ⎠
c) (− 125)− d) (8)−
1 2
3 = 3 =
−3
⎛1⎞ 2
f) (− 32)−
2
e) ⎜ ⎟ = 5 =
⎝4⎠

Ejercicio N°5: Aplica propiedades para resolver los siguientes ejercicios:
3 −1 1
1
−2
2 ⎛4⎞ 4
⎛4⎞ ⎛4⎞ 4
a) 3 2
⋅3 ⋅3 5
⋅3 = b) ⎜ ⎟ ⋅⎜ ⎟ ⋅⎜ ⎟ =
⎝9⎠ ⎝9⎠ ⎝9⎠
d) (− 4) ÷ (− 4)
−2 −4 1
c) b 3
⋅ b −2 ⋅ b = 5 5 =

[ ]
4
1
e) ⎛ 32 2 ⎞ f) (− 25)
1 5 −4
⎜ ⎟ = 2
=
⎝ ⎠
2 −3 ⎛1⎞ ⎛1⎞
g) x 5
÷x 5
= h) ⎜ ⎟ -1
÷⎜ ⎟ - 2/3
=
⎝5⎠ ⎝5⎠

15


Ejercicio N°6: Resuelve:

a) 8
−2
3
+ (− 32 )
−2
5 = (
b) 8a 3 ÷ b 6 3 = )2
−2 −2
⎛ 8 ⎞ ⎛ 32 ⎞
( )
3 5 2
c) ⎜ ⎟ − ⎜− ⎟ = d) 64a 6 ÷ b 9 3
=
⎝ 27 ⎠ ⎝ 243 ⎠

Ejercicio N°7: Resuelve aplicando las propiedades correspondientes:

a) 3
64 = b) 5 ⋅ 2 ⋅ 10 =
c) 4
46 = d) 3 10
x 30 =
16 1 3
e) = f) 3 ÷ 49 =
81 7
5 3
g) 5
− 16 ⋅ 5 2 = h) 3 − =
8 4
11 1
i) − =
4 2

Ejercicio N°8: Escribe en notación científica los siguientes números:

a) 7980000000 = b) 0,00000000259 =
c) 0,00000007 = d) 7000000000000 =
e) 5789000 = f) 0,00015 =
g) 5800 = h) 79 . 10-10 =
i) 135 . 1010 =

Ejercicio N°9: Resuelve los siguientes cálculos y expresa los resultados en notación
científica:

a) 2,1 ⋅ 10 8 ⋅ 3 ⋅ 10 5 = b) (8 ⋅ 10 9 ) ÷ (2 ⋅ 10 7 ) =
c) (3,12 ⋅ 10 4 ⋅ 5 ⋅ 10 7 ) ÷ (15 ⋅ 10 3 ) = d) 5,2 ⋅ 10 9 ÷ 2,6 ⋅ 10 7 + 1,7 ⋅ 10 3 =

16


CAPITULO II: RAZÓN Y PROPORCIÓN NUMÉRICA
2.1- RAZÓN ENTRE DOS NÚMEROS:
a
La razón entre dos números a y b es el cociente , por ejemplo la razón entre 10 y 2 es 5,
b
10 0,15 1
ya que = 5 y la razón entre los números 0,15 y 0,3 es =
2 0,30 2
2.2- PROPORCIÓN NUMÉRICA:
Los números a, b, c y d forman una proporción si la razón entre a y b es la misma que
a c
entre c y d, es decir = , esto se lee de la siguiente manera: “a es a b como c es a d”.
b d
Por ejemplo, los números 2;5 y 8;20 forman una proporción, ya que la razón entre 2 y 5 es
2 8
la misma que la razón entre 8 y 20, es decir =
5 20
a c
En la proporción = hay cuatro términos; a y d se llaman extremos, c y b se llaman
b d
medios.

La propiedad fundamental de las proporciones es:
“En toda proporción, el producto de los extremos es igual al de los medios”.

2 8
Así en la proporción anterior = se cumple que el producto de los extremos da 2 . 20
5 20
= 40 y el producto de los medios da 5 . 8 = 40
a c
EN GENERAL: = ⇒ a⋅d = b⋅c
b d

2.3- MAGNITUDES DIRECTAMENTE PROPORCIONALES
Si dos magnitudes son tales que a doble, triple ... cantidad de la primera corresponde doble,
triple... de la segunda, entonces se dice que esas magnitudes son directamente
proporcionales.

17


Ejemplo 1:
Una bolsa de fertilizante (urea) pesa 20 Kg ¿Cuánto pesan 2 bolsas?
Un cargamento a granel de urea pesa 520 Kg ¿Cuántas bolsas se podrán llenar?

Número de 1 2 3 ... 26 ...
bolsas
Peso en Kg. 20 40 60 ... 520 ...

Para pasar de la 1ª fila a la 2ª basta multiplicar por 20
Para pasar de la 2ª fila a la 1ª dividimos por 20
1 2 3
= = = ...
Observa que 20 40 60

Las magnitudes número de bolsas y peso en Kg son directamente proporcionales.
La constante de proporcionalidad para pasar de número de bolsas a Kg es 20.

2.4- REGLA DE TRES SIMPLE DIRECTA
La regla de tres es una operación que consiste en encontrar el cuarto término de una
proporción, a la que solo se le conocen tres términos.
Puede ser simple cuando solamente intervienen en ella dos variables o compuesta cuando
intervienen tres o más variables.
Toda regla de tres presenta una incógnita y una hipótesis. La hipótesis está constituida por
los datos del problema que se conocen y la incógnita por el dato que se busca. De acuerdo a
la relación con la incógnita, puede ser directa cuando los aumentos en una variable
provocan aumento en la otra variable o inversa cuando los aumentos en una variable
provocan disminución en la otra variable.

Ejemplo 2:
Determine el % MS (materia seca) y de Humedad de un forraje, cuya alícuota de MV
(materia verde) fue de 250 g Se colocó en estufa obteniéndose un peso de la alícuota de 63
g de MS.
250 g---------- 100%
63
63 g ---------- x = ⋅ 100% = 25,2%
250
% de MS = 25,2 %
% de Humedad = 100 – 25,2 = 74,8 %

18


Ejemplo 3:
Un estudiante debe llegar a un campo para realizar una actividad práctica. Para ello debe
recorrer un trayecto de 85 Km. asfaltados y otro de 35 Km. de tierra.
Si éste en camino asfaltado viaja a 120 Km/h y en camino de tierra lo hace a 90 Km/h,
¿cuánto tardará en llegar al campo?
Primero calcularemos el tiempo para recorrer los 85 kilómetros de asfalto y luego el
tiempo para recorrer los 35 kilómetros de tierra.
Que la velocidad sea de 120 Km/h significa que en una hora recorre 120 Km, o dicho de
otro modo, para transitar los 120 Km. son necesarios una hora, si en lugar de 120 Km. el
estudiante tiene que hacer sólo 85 Km., se puede plantear una sencilla regla de tres simple:
120 Km 85 Km
=
1h Xh
solo queda despejar la incógnita de esta ecuación, Si te animaste, debiste hacer un planteo
como el que sigue:
85Km ⋅1h
X = donde X = 0,708 h , o lo que es equivalente X = 42,48 min
120 Km
120 Km − − − − 1 h
85 Km − − − − X = ?
donde X = 0,708 h , o lo que es equivalente X = 42,48 min
Y ahora seguramente te ánimas a calcular el tiempo que te insumiría hacer los restantes 35
Km. de camino de tierra a 90 Km/h,
Entonces tus cálculos te tienen que haber dado como sigue:
90 Km − − − − 1 h
35 Km − − − − X = ?
donde X = 0,38 h o lo que es equivalente
1h − − − − 60 min
0,38h − − − − X = ?
donde X = 22,8 min .

Ejemplo 4:
La producción de materia verde de un campo en la zona de Río Cuarto es de
aproximadamente 42.500 kilogramos por hectárea y por año.
El porcentaje de agua de esa materia verde es de un 81,5 %, ¿Calcular los kilos de materia
seca (MS) presente en ella?

19


Interpretemos qué significa que la materia verde tenga un 81,5 % de agua, esto quiere decir
que por cada 100 Kg de materia verde tenemos 81,5 Kg de agua y 18,5 Kg de materia seca.
Como nos piden los kilogramos de materia seca por hectárea y por año caemos de nuevo en
una regla de tres:
1 00 % − − − − 42.500 Kg
18,5 % − − − − X = ?
donde X = 7862,5 Kg MS, este valor corresponde a la producción de materia seca de la
pradera.

Ejemplo 5:
En un lote destinado a la siembra de maíz se realiza un análisis de suelo que tiene en tantos
resultados una deficiencia de fósforo, para ello un ingeniero agrónomo aconseja fertilizar
poniendo 20 kilogramos de fósforo por hectárea, si el lote posee una superficie de 84
hectárea, ¿Cuántos kilogramos tendrá que poner el lote?
1 ha − − − − 20 Kg de fósforo
84 ha − − − − X = ?
donde X = 1680 Kg de fósforo.

2.5- PORCENTAJE
En casi todas las asignaturas que curses a lo largo de estos años vas a tener que trabajar con
porcentajes pero entonces ¿Qué es porcentaje?
En líneas generales podemos decir que porcentaje “es una parte de un todo”, por ejemplo:
Si vos tenés una pizza de 8 porciones y te comes 2 porciones, te estás comiendo el 25 % de
tu pizza.
Es muy común que los porcentajes se representen en diferentes formas gráficas acá te
mostramos una de ellas Diagrama de Torta:

Trabajar con porcentajes implica simplemente resolver una regla de tres. Te presentamos
algunos conceptos básicos.

20


Ejemplo 6:
Un cabañero tiene 180 vacas de la raza Hereford y quedan preñadas 140, el índice de
preñez es el porcentaje de animales que quedaron preñados respecto del total de animales
que fueron servidas y viene dado por:
180 Vacas − − − − 100 %
X = 77,7 %
140 Vacas − − − − X = ?
Mientras que para calcular el índice de parición se procede de forma similar a la anterior,
pero ahora es el porcentaje de animales vivos nacidos respecto del total que nacieron, con
lo que:
140 Terneros − − − − 1 00 %
130 Terneros − − − − X = ?
X = 92,85 % éste será el índice de parición.


Ejercicio N°1:
Se necesita comprar herbicida, para pasar en un lote con yuyo colorado, el producto
comercial está formulado al 42,5 % v/v, esto quiere decir que por cada 100 ml de solución
(herbicida) tenemos 42,5 ml del principio activo (soluto). Además se sabe que el volumen
de principio activo recomendado a emplear es de 0,9 litro por hectárea, si el lote tiene 90
hectáreas ¿cuántos litros de herbicida se necesitarían?

Ejercicio N°2:
Las dimensiones de un lote son de 1x103 por 1x103 m o de 1Km por 1 Km, si la cantidad de
surcos a sembrar es de 1923 y por cada pasada del tractor se siembran 14 surcos ¿Podrías
calcular cuántas veces tiene que pasar el tractor para cubrir todo el lote?.

Ejercicio N°3:
¿Cuál es el tiempo que demora en realizar una pasada el tractor del ejercicio anterior si
sabemos que este avanza a 4,5 Km/h y la longitud de cada pasada (el largo del lote) es de 1
Km?

Ejercicio N°4:
Un veterinario tiene que vacunar un grupo de 5 novillos, que poseen problemas
respiratorios, de 90 Kg de peso vivo cada uno. Para ello vacuna con un antibiótico de la

21


marca Nuflor, las dosis recomendadas son dos con un intervalo de 48 horas y el volumen es
de 1 ml por cada 15 Kg de peso vivo. ¿Cuántas dosis tiene que poner el veterinario? Si el
frasco viene en una presentación de 100 ml, ¿Cuantos debo comprar?.

Ejercicio N°5:
Si tenemos un potrero de 20 metros por 36 metros, y se necesita alambrarlo con 5 hilos
¿Cuantos metros de alambre debemos compra? Tener en cuenta que el lote tiene una
tranquera de 4 metros de largo.

Ejercicio N°6:
Para saber la capacidad de un tanque australiano se aplica la siguiente formula:

Volumen (lt ) = π ⋅ radio 2 ⋅ altura del agua = π ⋅ diametro 2 ⋅ altura / 4
Si queremos tener un tanque con una capacidad de 10.900 litros y un diámetro es de 3,74
metros, ¿Qué altura deberá tener?

Ejercicio N°7:
Cuando la mosca de los cuernos comienza a afectar a los vacunos, los veterinarios
recomiendan vacunar con una dosis de 10 centímetros cúbicos por cabeza. Si el bidón en el
cual viene este antiparásito es de 1,5 litros y se tiene una población de 2149 vacunos
¿Cuantos bidones se tendrán que comprar?

Ejercicio N°8:
En relación al ejercicio anterior; si se gastan 925 cm3 del antiparásito ¿Cuál es el porcentaje
que queda en el bidón?

22


CAPITULO III: ECUACIONES

3.1- EL MISTERIO DE LAS ECUACIONES
Antes de hablar de ecuaciones necesitamos identificar el concepto de igualdad.
Llamamos igualdad a elementos que tienen el mismo significado, como podemos ver en los
siguientes ejemplos:
3 + 2 = −5 − 10 ⋅ (−1) = 9 − 4
En cada igualdad hay 2 miembros separados por el signo =
• Primer miembro: en el primer ejemplo es 3 + 2; en el segundo, − 5 − 10 ⋅ (−1)
• Segundo miembro: en el segundo, 9 - 4.
Ahora que conocemos las igualdades, podremos desarrollar el concepto o la definición de
ecuación.

3.2- DEFINICIÓN
Los métodos para resolver ecuaciones datan de los tiempos de los babilonios (2000 a.C.).
La forma que tenemos de enunciar que dos cantidades o expresiones son iguales es
mediante una ecuación (o igualdad). Podemos entonces definir a las ecuaciones como una
igualdad entre expresiones algebraicas (sucesión de términos constituidos de números y
letras, cada término es separado del otro por un signo "+" ó "-"), en la que intervienen una o
más letras llamadas incógnita (cuyo valor hay que averiguar). Las expresiones que están a
ambos lados del signo igual son los miembros de la ecuación: primer miembro el de la
izquierda, segundo miembro el de la derecha. Se denomina solución de una ecuación a un
valor o conjunto de valores de la incógnita (x), para los cuales se verifica la igualdad

Por ej. 2x - 3 = x + 5 que se denomina ecuación en x

Por ejemplo:
5 + x = 12
La x representa al número que sumado con 5 tiene como suma al 12. Para saber cuál es el
término que falta, en este caso aplicamos la operación inversa: sustracción.
x = 12 - 5
x=7
En esta ecuación el valor de x es 7, porque
5 + 7 = 12.

23


• Observamos que este enunciado tiene dos partes o expresiones separadas por el
signo =, una en el lado izquierdo (LI), y otra en el lado derecho (LD).
• Es una expresión de igualdad con una variable, la x.
• La solución, o raíz, de la ecuación es un número a que produce una expresión cierta
al sustituirlo por la x, es decir a satisface la ecuación.
• Llamamos ecuaciones equivalentes a un conjunto de ecuaciones que tienen
exactamente las mismas soluciones.
• Resolver una ecuación consiste en hallar todas las soluciones de dicha ecuación.
• Una ecuación algebraica en x contiene sólo expresiones algebraicas como
polinomios, expresiones racionales, radicales y otras.
• Si todo número de los dominios de las expresiones de una ecuación algebraica es
una solución, la ecuación se denomina identidad, por ej. x2+2x+1 = (x+1)2.
Si hay números que no sean solución, la expresión se llama simplemente
ecuación, por ej. 5x-10 = 2x+8.
• Dos ecuaciones se llaman equivalentes si tienen las mismas soluciones o ambas
carecen de solución. Así, la ecuación 3x – 7 = x + 1 es equivalente a 2x – 8 = 0
porque ambas tienen como solución única x = 4.

3.3- RESOLUCIÓN DE ECUACIONES
Resolver una ecuación es hallar su solución (soluciones), o podemos llegar a la conclusión
que no tiene solución. Para resolver una ecuación, se pasa a otra equivalente cuya
apariencia sea más sencilla. Para averiguar el valor de x debe despejarse la letra incógnita.
Para ello nos valemos de una propiedad matemática (propiedad uniforme) que nos permite
poner un mismo número en ambos miembros de la expresión algebraica, siempre y cuando
se mantenga la igualdad.
Sin embargo, hay tipos de ecuaciones para cuya resolución se requieren técnicas especiales.
Es el caso, por ejemplo, de las ecuaciones cuadráticas y bicuadradas.
¨Generalmente, para resolver ecuaciones, elaboramos una lista de ecuaciones equivalentes
(cada una más sencilla que la precedente), terminando con una ecuación cuya solución
podemos hallar con facilidad¨.

- Podemos sumar o restar la misma expresión en ambos lados de la ecuación.
- Podemos multiplicar o dividir ambos lados de una ecuación por una expresión
que representa un número real distinto de cero.

24


MÉTODO :
- Eliminamos paréntesis
- Eliminamos denominadores
- Agrupamos términos semejantes
- Despejamos la variable
- Comprobamos la solución

Si hay, eliminamos todos los niveles de paréntesis que aparezcan comenzando por
el más interno, resolviendo las operaciones indicadas.
Si hay, eliminamos todos los denominadores multiplicando por el m.c.m.(de los
denominadores) ambos lados de la ecuación.
Agrupamos las expresiones con la variable en un lado (generalmente el izquierdo) y
las expresiones numéricas en el otro lado.
Despejamos la variable, obteniendo así la solución.
Comprobamos si la solución satisface la ecuación propuesta, es decir si aparece una
identidad verdadera.
Si una ecuación contiene expresiones racionales, a menudo eliminamos
denominadores multiplicando ambos lados por el m.c.m. de estas expresiones. Si
multiplicamos ambos lados por una expresión que es igual a cero para algún valor
de x, quizá la ecuación resultante no equivalga a la original.

6⋅x−7 = 2⋅x+5 (8⋅ x − 2) ⋅ (3⋅ x + 4) = (4 ⋅ x + 3) ⋅ (6 ⋅ x − 3)
6⋅x− 2⋅x = 5+ 7 24⋅ x2 + 32⋅ x − 6 ⋅ x − 8 = 24⋅ x2 −12⋅ x +18⋅ x − 9
4 ⋅ x = 12 26⋅ x − 6 ⋅ x = −9 + 8
12 12⋅ x = −1
x =
4 −1
x=
x = 3 12

3⋅ x 6
= 1+ 3 5 2
x−2 x−2 − =
2⋅ x − 4 x + 3 x − 2
3⋅ x 6 3 ⋅ ( x + 3) − 5 ⋅ (2 ⋅ x − 4) = 2 ⋅ (2 x + 6)
⋅ ( x − 2) = 1 ⋅ ( x − 2) + ⋅ ( x − 2)
x−2 x−2
3 ⋅ x + 9 − 10 ⋅ x + 20 = 4 ⋅ x + 12
3 ⋅ x = ( x − 2) + 6
− 11⋅ x = −17
2⋅ x = 4
17
x = 2 → No valida x=
11

25


¡¡¡cuidado!!!!!! El m.c.m. es (2x-4)(x+3), luego los
No se permite la división por cero, x=2 números 2 y -3 si aparecen en la solución
no es una solución, por tanto la ecuación no serían válidos, pero no es el caso.
dada no tiene soluciones.

3.4- TIPOS DE ECUACIONES
Las ecuaciones con una incógnita suelen tener un número finito de soluciones, mientras que
en las ecuaciones con varias incógnitas encontramos infinitas soluciones, las que suelen ser
estudiadas cuando forman sistemas de ecuaciones.

A las ecuaciones polinómicas de primer grado, ax + b = 0, se las llama lineales.
5x + 7 = 3 (es lineal).
(x – 5)2 + 3 = x2 – 1 (No hay que dejarse engañar por las apariencias, esta ecuación también
es lineal. Al desarrollar y simplificar se obtiene: –10x + 29 = 0).
A las ecuaciones polinómicas de segundo grado que responden a la estructura: ax2 + bx + c
= 0, se las denomina cuadráticas. Son ecuaciones de este tipo: x2+5x+3, ó (x – 2)2 + 7x
=5 + x. (En este caso, se despeja x de manera que al final queda una ecuación cuadrática, o
sea, un polinomio de grado dos).
Las ecuaciones radicales son aquellas en las que la incógnita está bajo un signo radical,
como
2 ⋅ x −1 = 3
Las ecuaciones racionales son ecuaciones en las que aparecen cocientes de polinomios; por
ejemplo:
1 2 5
+ = 2
x −1 x +1 x −1
En las ecuaciones exponenciales la incógnita está en un exponente: 2x = 8
En las ecuaciones logarítmica (inversa de las de tipo exponencial) la incógnita se encuentra
afectada por el logaritmo, acordarse que la solución debe estar de acuerdo con el dominio
de la función logarítmica): Log (x + 1) = 10.

26


3.5- SISTEMA DE ECUACIONES:
Conjunto de ecuaciones cuyas soluciones comunes se pretende hallar. Para indicar que
varias ecuaciones forman un sistema, se abarca el conjunto de todas ellas con una llave.
Sistemas de Ecuaciones Lineales:
Una ecuación con varias incógnitas es lineal si es de la forma ax + by = c, ax + by + cz
= d,…, es decir, si las incógnitas aparecen elevadas a la potencia 1 (sin exponentes).
Un sistema de ecuaciones lineales compatible o bien tiene solución única (es determinado),
o tiene infinitas soluciones (es indeterminado).
Existen varios métodos elementales para resolver sistemas de ecuaciones: el método de
sustitución, el método de igualación y el método de reducción. A continuación se aplican en
la resolución de sistemas de dos ecuaciones con dos incógnitas.
El método de sustitución consiste en despejar una de las incógnitas en una de las
ecuaciones y sustituir su expresión en la otra, la cual se transformará en una ecuación con
una incógnita que se puede resolver. Una vez conocido el valor de dicha incógnita se
obtiene, de inmediato, el valor de la otra.
Para resolver el sistema
⎧2 ⋅ x − 5 ⋅ y = 16
⎨
⎩4 ⋅ x + y = 10
por el método de sustitución conviene despejar la y de la segunda ecuación:
y = 10 − 4 ⋅ x (ahora se sustituye su valor en la primera)  2 ⋅ x − 5 ⋅ (10 − 4 ⋅ x) = 16
Se resuelve la ecuación resultante, pues sólo tiene una incógnita:
2 ⋅ x − 50 + 20 ⋅ x = 16 ⇒ 22 ⋅ x = 66 ⇒ x = 66 ⇒ x=3
22
Ahora el valor de x se sustituye en la expresión de y obtenida antes:
y = 10 – 4x = 10 – 4 · 3 = 10 – 12 = – 2
Se ha obtenido así la solución x = 3, y = – 2.
El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones e
igualar sus expresiones, obteniendo así una ecuación con una incógnita. Una vez resuelta se
obtiene fácilmente el valor de la otra incógnita.
Para resolver por igualación el sistema anterior, se puede despejar x ó y en ambas
ecuaciones e igualar sus expresiones:
(despejamos x en cada una de las expresiones para igualarlas y de esa manera poder hallar
el valor de y)

27


16 + 5 ⋅ y ⎫
x= ⎪ 16 + 5 ⋅ y 10 − y
2 ⎪
⎬ = ⇒ 4 ⋅ (16 + 5 ⋅ y ) = 2 ⋅ (10 − y ) ⇒ 64 + 20 ⋅ y = 20 − 2 ⋅ y ⇒
10 − y ⎪ 2 4
x= ⎪
4 ⎭
⇒ 20 ⋅ y + 2 ⋅ y = 20 − 64 ⇒ 22 ⋅ y = −44 ⇒ y = − 44 ⇒ y = −2
22
Por último, se sustituye el valor de y en alguna de las expresiones de x y se obtiene la
solución x = 3, y = – 2.
El método de reducción consiste en procurar que una de las incógnitas tenga el mismo
coeficiente en las dos ecuaciones para que, al restarlas miembro a miembro, se elimine
dicha incógnita, dando lugar a una ecuación con sólo la otra incógnita. Se resuelve dicha
ecuación y el valor de la incógnita se sustituye en una de las ecuaciones primitivas, y con
ello se puede obtener el valor de la otra incógnita.

3.6- RESOLUCIÓN DE ECUACIONES RACIONALES:
En este caso tenemos "fracciones" con polinomios. Se recomienda factorizar siempre el
denominador para poder buscar el denominador común y reducir la operación a un
polinomio (generalmente de primer o segundo grado) al que se lo resuelve como una
ecuación común.
Pongamos un ejemplo:
1 2 5
+ = 2
x −1 x +1 x −1
Factorizando:
Como no se repite ningún binomio en la suma, tomamos ambos como "común
denominador". Se opera igual que en una suma de fracciones, se divide ( x − 1) ⋅ ( x + 1) por
cada uno de los denominadores y el resultado se lo multiplica por el numerador.
Se simplifican los denominadores quedando una ecuación lineal.
Se despeja x.

28


1 2 5
+ = 2
x −1 x +1 x −1
1 2 5
+ =
x − 1 x + 1 ( x − 1) ⋅ ( x + 1)
1⋅ ( x + 1) + 2 ⋅ ( x − 1) 5
=
( x − 1) ⋅ ( x + 1) ( x − 1) ⋅ ( x + 1)
( x + 1) + 2 ⋅ ( x − 1) = 5
x +1+ 2 ⋅ x − 2 = 5
3⋅ x = 5 −1+ 2
3⋅ x = 6
x=6 3
x=2


Ejercicio Nº 1: Hallar el conjunto solución de las siguientes ecuaciones lineales.

a) 3.x + 2 = 7
b) x+3=x+3
c) –x+5=0
d) x + 7 – 3.x = 2.x +1
e) x+3–5=x
f) 5.x = 6

Ejercicio Nº 2: Resolver las siguientes ecuaciones:

4.x − 2
a) = x+3
5
3 ⋅ (x − 2)
b) = 4 ⋅ x −1
5
x − 2 2⋅ x −5
c) =
3 4

x−3
d) 2 − = 3 ⋅ ( x − 5)
4
x −3
e) −1 = 2 ⋅ x + 3
4

29


x x x
f) + − +1 = 2
4 3 2
2 ⋅ x x −1
g) − =1
3 4
3⋅ x −1 2 ⋅ x + 3
h) + =5
4 2
2 ⋅ x − 4 x −1 x − 3
i) − = −1
5 6 2
2 4
j) =
x − 5 3⋅ x + 7

1 1
k) = −5
2⋅ x − 6 2
3 x 2 +1 x +1
l) − + =0
1+ x 1− x 2 1− x
2 ⋅ x −1 10 1+ 2 ⋅ x
m) − =
2 ⋅ x +1 4 ⋅ x −1 1− 2 ⋅ x
2

Ejercicio Nº 3: Resolver los siguientes sistemas de ecuaciones
⎧2 ⋅ x − 3 ⋅ y = 0 ⎫
a) ⎨ ⎬
⎩4 ⋅ x + y = 14 ⎭
⎧2 1 ⎫
⎪ ⋅ x + ⋅ y = 5⎪
b) ⎨ 3 4 ⎬
⎪2 ⋅ x − y = 6 ⎪
⎩ ⎭
⎧x +1 y − 4 ⎫
⎪ 10 + 6 = x − 1 ⎪
⎪ ⎪
c) ⎨ ⎬
⎪ x + 5 − y − 7 = 3 ⋅ y − x⎪
⎪ 7
⎩ 3 ⎪
⎭
⎧2 ⋅ x − 3⋅ y 3⋅ x + y 7⎫
⎪ + =− ⎪
⎪ 4 3 3⎪
d) ⎨ ⎬
⎪x + 2⋅ y − 5⋅ x + 2⋅ y = 5 ⎪
⎪ 3
⎩ 4 4 ⎪
⎭

Ejercicio Nº 4:
El triplo de un número es igual al número aumentado en 8. Hallar el número.

30


Ejercicio Nº 5:
Cuatro veces un número es igual al número aumentado en 30. Hallar el número.

Ejercicio Nº 6:
En un gallinero hay gallinas y conejos. ¿Cuántos animales hay de cada clase si hay 144
patas y 50 cabezas?

Ejercicio Nº 7:
Un estanciero vendió los 5/7 de su tropilla de caballos; en seguida compró 12; teniendo
entonces 48 caballos menos que al principio. ¿Cuántos tenía antes de la primera venta?

Ejercicio Nº 8:
La capacidad efectiva (Ce) de una maquinaria agrícola, que es el tiempo que tardara una
maquina en trabajar una superficie exacta y conocida, cuya ecuación es la siguiente:
Ce(ha / hora) = a(m) ⋅ v(km / hora) ⋅ r ⋅ 0,1
Donde a = ancho efectivo (ancho realmente cubierto por cada pasada), v = velocidad, r =
coeficiente de tiempo efectivo, 0,1 coeficiente para adecuar unidades.
Si v =1 m/s, Ce = 4,8 y a = 6 m. ¿Cuál será el valor del coeficiente de tiempo efectivo?

Ejercicio Nº 9:
Uno de los insectos defoliadores más importantes es la oruga lagarta, se alimenta de plantas
de sombra, de bosque y de árboles frutales. Una persona vive en un área en la que oruga se
ha convertido en un problema y desea rociar los árboles de su propiedad antes de que
ocurra una mayor defolación. Necesita 128 onzas de una solución compuesta de 3 partes de
insecticida A y 1 parte de insecticida B. Después de preparada la solución se mezcla con
agua. ¿Cuántas onzas de cada insecticida deben ser usadas?

Ejercicio Nº 10:
Existen varias reglas para determinar las dosis de medicina para terneros especificadas las
de los novillos. Tales reglas pueden basarse en el peso, la altura a la cruz, etc. Si A= edad

31


del ternero (años) , D= dosis para novillo y C= dosis para terneros (en años), ¿a que edad la
dosis para terneros es la misma usando estas reglas? A continuación se presentan dos reglas
para el cálculo
A⋅ D
Re gla de Young C=
12
A +1
Re gla de Covulinig C = ⋅D
24

Ejercicio Nº 11:
El perímetro de un lote rectangular que va a ser alambrado es de 200 pies y su largo es 3
veces el ancho. ¿Determine las dimensiones del lote?

Ejercicio Nº 12:
Para regular su temperatura en relación con el calor ambiental, las ovejas aumentan su
ritmo respiratorio r (por minuto) cuando la longitud de la lana l (en centímetros) disminuye.
Supongamos que una oveja con una longitud de lana de 2 cm tiene un ritmo (promedio)
respiratorio de 160, y aquellas con una longitud de lana de 4 cm tienen un ritmo respiratorio
de 125. Supongamos que ``r`` y ``l`` están relacionadas linealmente (a) determine el ritmo
respiratorio de una oveja con una longitud de lana de 1 cm y (b) determine la longitud de la
lana si el ritmo respiratorio es de 105.
∆y ∆y 160 − 125 160 − 125
Ayuda: r= ⋅ l + B donde = , B = 160 − ⋅2
∆x ∆x 2−4 2−4

Ejercicio Nº 13:
En una granja de 1000 acres se siembra maíz y soja. El costo por acre para cultivar maíz es
de U$U 65 y para la soja de U$U 45. Si el presupuesto disponible es de U$U 54.325 y hay
que utilizar todo el terreno ¿cuántos acres se deben asignar a cada cultivo?

32


Ejercicio Nº 14:
Un aspersor que rocía agua con un patrón circular es colocado en el centro de un terreno
cuadrado con área de 1250 pies2. ¿Cuál es el radio más pequeño que puede usarse si el
campo debe estar totalmente contenido dentro del circulo?, ¿Cuál es la superficie de más
que estoy fulmigando?
Ayuda: calculo de la hipotenusa de un triángulo rectángulo (cateto más largo)

hip 2 = a 2 + b 2

33


CAPITULO IV: UNIDADES
“Cuando se puede medir aquello de que se habla y expresarlo en números se sabe algo acerca de ello; pero nuestro
saber es deficiente e insatisfactorio mientras no seamos capaces de expresarlo en números, lo otro puede significar el
comienzo del conocimiento, pero nuestros conceptos apenas habrán avanzado en el camino de la Ciencia...”

Lord Kelvin.

4.1- SISTEMAS DE UNIDADES
Llamamos magnitud a cualquier propiedad física susceptible de ser cuantificada
objetivamente en el proceso de medición.
Medir es comparar una magnitud con otra de su misma especie que se toma como unidad.
En toda medición intervienen necesariamente dos partes: el sistema que queremos medir y
el aparato de medida. Es importante reconocer que por mucho cuidado que pongamos en
realizar una medida, nunca obtendremos el valor exacto de una magnitud, por ello todas las
medidas están afectadas por un error.
En la XIV Conferencia General del Comité Internacional de Pesas y Medidas (1971) se
decidió adoptar un conjunto de magnitudes fundamentales (aquellas magnitudes que no
pueden ser definidas o expresadas a partir de otras) de tal manera que todas las demás,
llamadas magnitudes derivadas, pudieran expresarse en función de las primeras. Además
se adoptaron también las unidades correspondientes a cada una de las magnitudes
fundamentales, este proceso dio origen a lo que conocemos como Sistema Internacional,
abreviadamente SI (del francés Système International d’Unités).
El SI fue adoptado en casi todos los países salvo los de lengua inglesa, donde se utilizan
por norma las unidades británicas. Cabe aclarar que en el trabajo científico se emplean en
todo el mundo unidades del SI aunque es necesario a veces realizar el pasaje de un sistema
a otro, este mecanismo será descrito oportunamente en este capítulo.
A continuación se muestran las magnitudes fundamentales junto a sus unidades básicas en
el sistema Internacional:
Magnitud Unidad Símbolo unidad Símbolo dimensión

Longitud metro m L

Masa kilogramo Kg M

Tiempo segundo s T

Intensidad eléctrica amperio A A

Temperatura kelvin K K

Cantidad de sustancia mol mol S

Tabla Nº1: Magnitudes Fundamentales del Sistema Internacional

34


4.2- EL PATRÓN DE LONGITUD:
El metro es la longitud de trayecto recorrido en el vacío por la luz durante un tiempo de
1/299.792.458 de segundo. El resto del sistema métrico se puede derivar simplemente del
metro, las áreas se miden en metros cuadrados, los volúmenes se miden en metros cúbicos,
etc. El litro es una medida métrica de volumen de uso común. Equivale a la capacidad de
una décima de un metro cúbico. Hay por consiguiente 1000 litros en un metro cúbico.
4.3- EL PATRÓN DE MASA:
El kilogramo (Kg) es igual a la masa del prototipo internacional del kilogramo. La
verdadera norma de peso está representada por el peso de una barra de una aleación de
iridio y platino que se conserva en París. Los pesos se definen tomando un volumen
unitario y llenándolo con agua. Un metro cúbico de agua es igual a una tonelada métrica.
Un centímetro cúbico de agua es igual a un gramo. Un decímetro cúbico de agua es
equivalente a un kilogramo. Un litro de agua es equivalente a un kilogramo, puesto que el
volumen de un litro es un decímetro cúbico.
4.4- EL PATRÓN DE TIEMPO:
El segundo (s) es el tiempo ocupado por 9.192.631.770 vibraciones de la radiación (de una
longitud de onda específica) emitida por un átomo de cesio.
Además de las unidades básicas existen lo que se denomina “Unidades SI derivadas” se
definen de forma que sean coherentes con las unidades básicas. Varias de estas unidades SI
derivadas se expresan simplemente a partir de las unidades SI básicas. Otras han recibido
un nombre especial y un símbolo particular.
TABLAS
A continuación se muestran tablas con las unidades derivadas y su representación en el
sistema internacional
Magnitud Nombre Símbolo
Superficie Metro cuadrado m2
Volumen Metro cúbico m3
Velocidad Metro por segundo m/s
Aceleración Metro por segundo cuadrado m/s2
Masa en volumen Kilogramo por metro cúbico Kg/m3
Velocidad angular Radián por segundo Rad/s
Aceleración angular Radián por segundo cuadrado Rad/s2
Tabla Nº2: Magnitudes Derivadas del Sistema Internacional

35


Tabla No 3: Las unidades del sistema internacional derivadas con
nombres y símbolos especiales.
Expresión en otras Expresión en
Magnitud Nombre Símbolo
unidades SI unidades SI básicas
Frecuencia Hertz Hz s-1
Fuerza Newton N m·Kg·s-2
-2
Presión Pascal Pa N·m m-1·Kg·s-2
Energía, trabajo, cantidad de
Joule J N·m m2·Kg·s-2
calor
Potencia Watt W J·s-1 m2·Kg·s-3
Cantidad de electricidad Coulomb C s·A
carga eléctrica
Potencial eléctrico Volt V W·A-1 m2·Kg·s-3·A-1
fuerza electromotriz
Resistencia eléctrica Ohm Ω V·A-1 m2·Kg·s-3·A-2
Capacidad eléctrica Farad F C·V-1 m-2·Kg-1·s4·A2
Flujo magnético Weber Wb V·s m2·Kg·s-2·A-1
Inducción magnética Tesla T Wb·m-2 Kg·s-2·A-1
Inductancia Henry H Wb·A-1 m2·Kg s-2·A-2
Tabla Nº3: Magnitudes Derivadas del Sistema Internacional con Nombres Propios.

Los prefijos, como kilo, deci, etc., se usan mucho en el sistema métrico. Un prefijo indica la
multiplicación o división de la unidad básica por 10 ó uno de sus múltiplos, 100, 1000, etc.
Los prefijos utilizados se describen en la siguiente tabla:

Aumentativos Diminutivos
x 10 Deca da x 10-1 Deci d

x 102 Hecto h x 10-2 Centi c

x 103 Kilo K x 10-3 Mili m

x 106 Mega M x 10-6 Micro µ

x 109 Giga G x 10-9 Nano N

x 1012 Tera T x 10-12 Pico P

x 1015 Peta P x 10-15 Femto F

Tabla Nº4: Prefijos del Sistema Internacional.

36


4.4- INTRODUCCIÓN AL ANÁLISIS DIMENSIONAL.

Asociada con cada cantidad medida hay una dimensión, como lo muestra la tabla Nº1.
Toda ecuación debe ser dimensionalmente compatible, es decir, las dimensiones en ambos
lados de la ecuación deben ser las mismas.
La atención a las dimensiones puede a menudo evitar que se cometan errores al escribir las
ecuaciones.
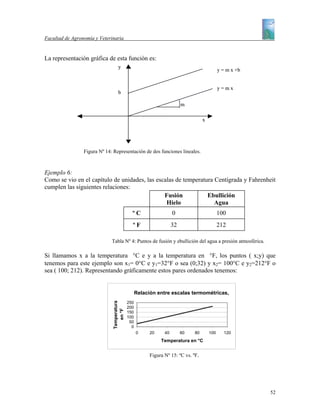
Como ejemplo, consideremos que se dispone de la siguiente ecuación para calcular la
l l
superficie de un potrero: S = l1 l 2 + 3 2
2

La representación esquemática del mismo puede verse en la figura Nº1:
l1

l2

l3

Figura No 1

Si los lados (l) están en metros y debido a que la dimensión correspondiente es L
podríamos expresar:
l3 ⋅ l 2
S = l1 ⋅ l 2 +
2
[S ] = [m 2 ]= L ⋅ L + L ⋅ L
[S ] = L2 + L2
[S ] = L2
↓ ↓
[m ] = [m ]
2 2

Esto está de acuerdo con las unidades de superficie expresadas en la tabla N° 2.
l
Si la ecuación hubiese estado escrita de la siguiente manera: S = l1 ⋅ l 2 + 3 el análisis
2
dimensional sería de utilidad para poner en evidencia el error, esto es:

37


l3
S = l1 ⋅ l 2 +
2
[S ] = [m 2 ]= L ⋅ L + L
[S ] = L2 + L
↓ ↓
[m ] = [m ]+ [m]
2 2

144 2444
4 3
ERROR

4.6- CAMBIO DE UNIDADES
Existen dos formas de trabajar con el cambio de unidades, la primera de ella utiliza la regla
de tres y en la segunda se recurre al hecho de que cualquier cantidad puede ser multiplicada
por 1 sin que ésta cambie su valor. Explicaremos a continuación esta segunda forma de
trabajo.

Supongamos que un animal corre a una velocidad de 45 km/h y se desea convertir este
valor a m/min, veamos como es posible efectuar este cambio.
Como 1000 m = 1 km y además 1 h = 60 min podemos plantear:
k m 1000 m 1h 1000m 1h
Velocidad = 45 notar que = 1 y que =1
h 1 k m 60 min 1 km 60 min
m
con lo que: Velocidad = 750
min

Aunque por lo general utilizamos unidades del SI, en ocasiones necesitamos cambiar
unidades de éste al sistema de unidades británicas o viceversa, para ello se debe disponer
de una “Tabla de Conversión de Unidades”.
A continuación se adjuntan las principales tablas de conversión de unidades:

LONGITUD
Centímetro Metro Kilómetro Pulgada (in) Pie (ft) Milla (mi)
-2
1 centímetro = 1 10 10-5 0,3937 3,281x10-2 6,214x10-6
1 metro = 100 1 10-3 39,37 3,281 6,214x10-4
1 kilómetro = 105 1.000 1 3,937x104 3281 0,6214
-2 -5
1 pulgada (in) = 2,540 2,540x10 2,540x10 1 8,333x10-2 1,578x10-5
1 pie (ft) = 30,48 0,3048 3,048x10-4 12 1 1,894x10-4
1 milla (mi) = 1,609x105 1.609 1,609 6,336x104 5.280 1

Tabla Nº5: Tabla de conversión para longitud.

38


MASA
gramo kilogramo Onza (oz) Libra (lb) Tonelada (ton)
1 gramo = 1 0,001 3,527x10-2 2,205x10-3 1,102x10-6
1 kilogramo = 1.000 1 35,27 2,205 3,125x10-5
1 onza = 28,35 2,835x10-2 1 6,250x10-2 1,830x10-30
1 libra = 453,6 0,4536 16 1 0,0005
1 tonelada = 1x106 1000 3,527x104 2.205 1
Tabla Nº6: Tabla de conversión para masa.

FUERZA
dina Newton (N) 1 kilogramo-fuerza (kgf)
1 dina = 1 10-5 1,020x10-6
1 Newton = 105 1 0,1020
1 kilogramo-fuerza = 9,807x105 9,807 1
Tabla Nº7: Tabla de conversión para fuerza.

ENERGÍA, TRABAJO, CALOR

Joule (J) Caloría (cal) Kilowatt-hora (kW.h)
1 Joule = 1 0,2389 2,778x10-7
1 caloría = 4,186 1 1,163x10-6
1 kilowatt-hora = 3,6x106 8,6x105 1
Tabla Nº8: Tabla de conversión para energía, trabajo y calor.

PRESIÓN
Centímetro de
Atmósfera Libra por pulgada2
mercurio Pascal
(atm) (lb/in2)
(cm Hg)
1 atmósfera = 1 76 1,013x105 2.116
1 centímetro de mercurio a
1,316x10-2 1 1333 27,85
0°C =
1 pascal = 9,869x10-6 7,501x10-4 1 2,089x10-2
1 libra por pulgada2 = 6,805x10-2 5,171 6,895x103 1
Tabla Nº9: Tabla de conversión para presión

POTENCIA
Libra-pie por Caballo de Caloría por segundo Watt (W)
segundo(ft.lb/s) fuerza(hp) (cal/s) (W=N.m/s)
1 libra-pie por segundo = 1 1,818x10-3 0,3239 1,356
1 caballo de fuerza = 550 1 178,1 745,7
1 caloría por segundo = 3,088 5,615x10-3 1 4,186
1 watt = 0,7376 1,341x10-3 0,2389 1
Tabla Nº10: Tabla de conversión para potencia.

39


TEMPERATURA

° F = 1,8 °C + 32 donde °F = Grados Fahrenheit y °C = Grados Celsius

°C = 0,555 (° F − 32)

° K = °C + 273,15 donde °K = Grados Kelvin
Tabla Nº11: Tabla de conversión para temperatura.

UNIDADES AGRARIAS DE USO CORRIENTE:
1 hectárea (ha) = 10.000 m2
100 hectáreas = 1 km2
1 quintal = 100 kg
1 hectárea = 2,471 acres = 107.640 pies
1 cm2 = 0,00155 pulgadas2
1 pie2 = 929 cm2 = 144 pulgadas2
1 kg/cm2 = 14,223 libras/pulgadas2
1 atmósfera = 1,033 kg/cm2
1 m3 = 1.000 litros
1 legua = 5 km
Tabla Nº12: Tabla de unidades agrarias comunes.

A continuación se ejemplifica su uso:
Un Ingeniero Agrónomo debe sembrar un lote de 100 ha con alfalfa, éste sabe que la
densidad de siembra de la misma es de 1,838 x10-3 lb/ft2. ¿Cuántos kilogramos de semillas
debe comprar?
Solución:

1,838 x10 −3
lb
= 1,838 x10 −3
lb 1 Kg (1 ft )2 10.000m 2
ft 2 ft 2 2,205 lb (0,3048m )2 1ha

−3 lb −3 lb 1 Kg 1 ft 2 10.000m 2
1,838 x10 = 1,838 x10
ft 2 ft 2 2,205 lb 0,0929m 2 1ha
lb Kg
1,838 x10 −3 = 89,73
ft 2 ha

Para 100 ha nos da un total de 8973 Kg de semillas.

40


4.7- EJERCICIOS DE APLICACION

Ejercicio Nº 1:
La potencia necesaria para que un colibrí pueda revolotear viene dada por la siguiente
expresión:

w3
P=
2 ρA

donde:
P = potencia en Kg m2/s3
w = Peso del pájaro.

ρ = Densidad del aire en Kg/m3.
A = Área barrida por las alas del animal en m2.
a) ¿En qué unidades debe estar expresado el peso del animal para que la ecuación sea
dimensionalmente correcta?

Ejercicio Nº 2:
La temperatura aproximada T de la piel en términos de la temperatura Te del medio
ambiente está dada por la siguiente ecuación:
T = 32,8 + 0,27(Te − 20)

donde ambas temperaturas están expresadas en grados centígrados.
a) ¿Que términos de la ecuación debería modificar si se tiene el valor de la temperatura
ambiente en °K?
b) ¿El primer término del segundo miembro es adimensional, o tiene unidades?, en caso de
tenerlas especifíquelas.

Ejercicio Nº 3:
Suponga que un indicador radioactivo, como un tinte colorante, se inyecta
instantáneamente al corazón de un animal en el tiempo t = 0 y se mezcla de manera
uniforme con la sangre dentro del corazón. Sea C0 la concentración inicial del indicador en
el corazón y suponga que el corazón tiene un volumen constante V. Conforme sangre fresca
fluye al corazón suponga que la mezcla diluida (de sangre e indicador) sale a una razón
constante positiva r. La concentración C(t) del indicador en el corazón en el tiempo t está
dada por la siguiente ecuación:

41


⎛ r⋅t ⎞
−⎜ ⎟
C (t ) = C 0 e ⎝V ⎠
⎛ r ⎞
−⎜ ⎟
a) ¿El término e ⎝ Vt ⎠ deberá tener unidades? Justifique con los cálculos que considere
necesarios.

b) Si C 0 está expresada en µg/l, ¿qué unidades tendrá C (t ) ?

c) ¿Podría expresar C (t ) en g/m3 si C 0 tiene las mismas unidades que en el inciso b?,
¿cómo quedaría la ecuación anterior?

Ejercicio Nº 4:
En un estudio sobre plantas arraigadas en cierta región geográfica, se determinó que en
terrenos de tamaño A (en metros cuadrados), el número promedio de especies encontradas
fue S y viene dado por:
S = 3,224 A
a) ¿Qué unidades tiene la constante 3,224?
b) ¿Cuántas plantas se encontrarán en 0,10 ha?
c) Si se ha encontrado un total de 8064 plantas, ¿cuántos acres se habrán estudiado?

42


CAPÍTULO V: FUNCIONES.

En este tema se retomará el concepto de función que se incorporó en el secundario para
luego profundizar sobre algunas funciones de utilidad en las Ciencias Agropecuarias.

5.1- INTRODUCCIÓN
Pensemos en dos conjuntos, el conjunto A y el conjunto B, donde algunos elementos del
conjunto A se “relacionan” con elementos del conjunto B. Esta situación se esquematiza en
la siguiente figura:
R
A B

Figura Nº 1: Representación esquemática de una relación.

Cuando necesitamos “vincular ó relacionar” elementos de dos conjuntos surge la idea de
Relación.
Como las flechas “parten” del conjunto A y “llegan” a B, estos conjuntos se llaman partida
y llegada de la relación respectivamente.
Observemos que pueden existir elementos del conjunto A que no están relacionados con
ningún elemento de B.
Entonces el conjunto de los elementos de la partida que están asociados a algunos de la
llegada, forman un subconjunto que se denomina Dominio de la relación.
Así como hemos agrupado los elementos que son “partida” de alguna flecha, agrupamos los
elementos que son llegada o “punta” de alguna flecha en el conjunto B para formar el
subconjunto de la llegada llamado Imagen de la relación.

Formalizando:
Una relación R de A en B hace corresponder a elementos del primer conjunto, elementos
del segundo conjunto.

El dominio y la imagen de la relación quedan definidos por comprensión de la siguiente
manera:

Dom (R) = {x∈ A / existe y ∈ B∧ x R y}
Img (R)={ y∈ B / existe x ∈ A ∧ x R y}

43


Esto se lee: el dominio de la relación está formado por x que pertenece al conjunto A, tal
que existe un y que pertenece al conjunto B y x está relacionado por la relación R con el
elemento y (del mismo modo se lee imagen de R).
Si ahora consideramos la siguiente figura:
f
A B

Figura Nº 2: Representación esquemática de una función.

En este caso vemos que el dominio de esta relación coincide con el conjunto de partida, es
decir de todos los elementos de la partida salen flechas.
Vemos además, que de cada elemento de la partida sale una sola flecha.
Concentraremos nuestra atención en estas relaciones particulares que tienen un nombre
especial, el de “FUNCIÓN”.

5.2- DEFINICION DE FUNCIÓN

Una función de A en B es una relación que asocia a cada elemento de A uno y solo uno
de B, llamado su imagen.

En síntesis:
De cada elemento de la partida salen flechas.
De cada elemento de la partida sale una sola flecha.
En base a la definición, los siguientes diagramas representan funciones.
1 2

3 4

Figura Nº 3: Representación esquemática de diferentes funciones.

44


A continuación damos expresiones en lenguaje coloquial y la correspondiente notación en
lenguaje simbólico:

1) “f es una función de A en B” ⇒ f: A→B
2) “ f hace corresponder al x ∈ A, el y ∈ B” ⇒ f: x→y
3) “ y es la imagen por f de x” ⇒ y = f(x)

5.3- FUNCIONES NUMÉRICAS

Veremos ahora algunas funciones particulares, las funciones numéricas, aquellas donde su
dominio e imagen están compuestos por números.

Ejemplo 1:
La población de vacas en un establecimiento ganadero según los años, a esta situación la
podemos expresar mediante tablas:

Año N° de Vacas
2000 180
2001 150
2002 200
2003 180
Tabla Nº1: Población de vacas.

Ejemplo 2:
La producción de leche en un tambo. Esta puede variar según la hacienda y también según
la época del año por lo tanto podemos tener así distintas funciones.

N° de Vacas Cantidad promedio de
Leche diaria ( lt/día)
15 300
20 400
Tabla Nº2: Población de vacas versus producción de leche.

Producción promedio
Mes De leche diaria de una vaca
(lt/ día)
1 20
2 23
3 21
4 19
5 20

45


6 18
7 17
8 22
9 23
10 19
11 20
12 17
Tabla N3: Producción de leche versus meses del año.

Como vemos en estos ejemplos las funciones van desde un conjunto de números (Reales o
Complejos) a otro conjunto también formado por números (Reales o Complejos). A estas
funciones que relacionan conjunto de números las llamaremos “funciones numéricas”, esto
es:

DEFINICIÓN:
Una función numérica es una regla que asocia a cada número del primer conjunto uno
y solo uno del segundo conjunto.

Ejemplo 3:
Si el conjunto A es igual al conjunto B y es igual al conjunto de los números naturales (o
sea A = B = Naturales) y la regla que asocia a ambos conjuntos es “a un número del primer
conjunto le asignamos su triplo”.
La representación es la siguiente:

A B
1 3

2 6
3 9
. .
. .
. .
x y =3x

Figura Nº4: Representación esquemática de una función numérica.

Vemos que es imposible completar los diagramas pues el conjunto de los números naturales
tiene infinitos elementos, por lo tanto es necesario especificar para un x genérico cual es el
y que le corresponde:

f: x→3x ó f (x) =3x ó y =3x

46


Observamos que y depende de x, por lo cual usualmente a x se la llama variable
independiente y a y variable dependiente.
En general suele darse solo la regla que asocia a un número x del dominio, uno de la
llegada, expresada mediante una ecuación sin especificar el dominio. En este caso, el
dominio se debe tomar como el mayor conjunto donde, dado x, podamos resolver las
operaciones indicadas.
Ejemplo 4:

1) Si f ( x ) = 2 x 3 − 3x 2 ó y = 2 x 3 − 3x 2 ⇒ Dom(f)={ todos los números
reales}

2) Si f ( x) = 2 x − 5 ó y = 2x − 5 ⇒ Dom(f)={ x ∈ Reales / 2x-5≥ 0}
o Dom(f)={ x ∈ Reales / x≥ 5/2}

ya que 2x-5 puede resolverse siempre, pero la 2 x − 5 existe solo si 2x-3≥ 0 (no podemos
resolver la raíz cuadrada de un número negativo ya que el resultado sería un número
complejo, no un número real).

5.4- REPRESENTACIÓN GRÁFICA
Si consideramos ahora la función real dada por el siguiente diagrama:
A B

1 1
1/ 2 ⇔ f ( x) = x 2 o y = x2
1/ 4

π/2
π 2 /4

2 4

Figura Nº 5: Representación esquemática de y = x
2

Vemos que la relación y = x , permite vincular un par de números, que es el par que
2

verifica la ecuación. Así, para cada x del dominio, tenemos el valor de y que le corresponde
al calcular el cuadrado.
Podemos indicar los pares: (1;1), (1/2 ; 1/4), (π/2 ; π2/4), (2 ; 4) escribiendo como primer
elemento uno del dominio y como segundo su imagen. Estos pares se denominan pares
ordenados y los elementos que lo forman, sus coordenadas.

DEFINICIÓN:
Un par ordenado es una dupla de elementos, denotado por (a;b), tal que (a;b) = (c;d) si y
solo si a=c y b=d.

47


Para representar gráficamente una función se toma un sistema de ejes cartesianos
ortogonales (dos rectas que se cortan formando 4 ángulos iguales, graduados en unidades
no necesariamente iguales). El punto de intersección es el origen del sistema y las flechas
indican el sentido positivo de los ejes.
En el eje horizontal llamado eje de las x ó eje de las abscisas, se ubican los puntos del
dominio y en la recta vertical, llamada eje de las y ó eje de las ordenadas, los elementos de
la imagen. Luego el par (a;b) corresponderá al punto del plano que se obtiene al intersecar
la recta vertical que pasa por a y la recta horizontal que pasa por b.

y
(a;b)
b

a
x
Figura Nº 6: Representación de un par ordenado.

Notar que estos dos ejes dividen al plano en cuatro cuadrantes, numerados en sentido
antihorario.
y

2do Cuadrante 1er Cuadrante

x

3er Cuadrante 4to Cuadrante

Figura Nº 7: Cuadrantes de un plano cartesiano.

Ejemplo 5:
Teniendo un gráfico ¿Cómo sabemos si corresponde o no a una función?
La respuesta se obtiene trazando una recta vertical, si ésta corta al gráfico mas de una vez
entonces no representa una función ya que para un mismo valor de x tendíamos más de un
valor de y.
En la figura Nº 8 se dan diferentes representaciones donde algunas de ellas corresponden a
funciones y otras no. Ahora, ¿Cuales de los siguientes gráficos corresponden a una
función?

48


1 y 2 y

x x

3 y 4 y

x x
Figura Nº 8: Gráficos de relaciones y funciones.

5.5- CLASIFICACIÓN PARA FUNCIONES REALES

Funciones crecientes y decrecientes.
Decimos que f(x) es una función creciente cuando, para un a < b se verifica que
f(a) <f(b).
y

f (b)

f (a)

a b
x
Figura Nº 9: Representación de una función creciente.

Y decimos que f(x) es una función decreciente cuando, para un a < b se verifica
que f(a) > f(b). y

f (a)
f (b)

a b
x
Figura Nº 10: Representación de una función decreciente.

49


Funciones pares e impares.
Decimos que f(x) es una función par si para todo x que pertenece al dominio se
verifica que
f(x) = f(-x).
y

Función par

f (x)
- f (x)
()
-x x x
Figura Nº 11: Representación de una función par.
Y decimos que f(x) es una función impar si para todo x que pertenece al dominio se
verifica que f(x) = -f(-x).

Algunas funciones que se utilizan frecuentemente en las Ciencias Agropecuarias:

5.6- LA FUNCIÓN LINEAL

Si se sabe que un pollo para consumo pesa 2,100 kg. ¿Cuántos pollos se deben comprar si
se quiere tener en total 10,5 kg.? El problema podría plantearse con una regla de tres, cuyo
resultado obvio sería 5 pollos. Pero si ahora si se compran por ejemplo 8 pollos, 9 pollos,
10 pollos, etc. y se desea saber cuantos kilogramos se tiene sería muy poco práctico
plantear una regla de tres para cada situación.
Una solución más simple es encontrar la función que relacione la cantidad de pollos con los
kg. Si recordamos lo que ya vimos sobre pares ordenados, podemos graficar los datos de
este problema de la siguiente forma:
Peso total de pollos

30
25
20
(kg)

15
10
5
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Cantidad de pollos

Figura Nº 12: Peso total vs. Cantidad de pollos.

50


La línea que une estos puntos será la función que vos estás buscando y tendrá la forma
y = mx, las ecuaciones de esta forma representan rectas que pasan por el origen, ya que si
no se compra ningún pollo la cantidad de kg. es cero, significa que la función lineal en este
caso pasa por el punto (0;0).
Así si es necesario saber cuantos kg. se tiene se traza una recta vertical, por ejemplo por 8
pollos, hasta cortar la gráfica y desde allí se traza una recta horizontal y se obtienen los kg.
deseados, o sea 16,8 kg.

Peso total de pollos
30
25
(kg) 20
15
10
5
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Cantidad de pollos

Figura Nº 13: Peso total vs. Cantidad de pollos para un valor particular de x.

Si ahora el peso de cada pollo fuera mayor ¿Cómo sería la recta? Si se analiza el gráfico se
vería que ésta sería más vertical, esto se debe a que en nuestro caso en la ecuación, y = m x,
“m” me da la inclinación o “pendiente” de la recta y representa el peso promedio de
cada pollo.
Podemos pensar ahora en independizarnos del gráfico, como ya sabemos que la función que
une estos dos puntos es:
y=mx o sea y = 2,100 ⋅ x

vemos que sin hacer el gráfico ni regla de tres, podemos saber los kg. que tenemos
solamente reemplazando la cantidad de pollos en x.
Por ejemplo si x =12 pollos:

y = 2,100 ⋅ 12 ⇒ y = 25,2 kg.

Este sencillo ejemplo ilustra claramente la utilidad de trabajar con funciones.
Cuando estudiamos algún fenómeno relacionado con la Ingeniería Agronómica o con la
Medicina Veterinaria, contar con la función que lo describe significa disponer de una
herramienta poderosísima para predecir o pronosticar que va a ocurrir.
En general las ecuaciones de la forma, y = mx +b, representan rectas. La inclinación de
estas rectas viene dada por su pendiente “m”. Para valores positivos de m, la recta es
creciente, y tanto más inclinada cuanto mayor es el valor de m. Para valores negativos de m,
la recta es decreciente, y tanto más inclinada cuanto mayor sea m en valor absoluto.
El corte de la recta con el eje y (cuando x = 0) viene dado por el valor de la “ordenada al
origen”, “b”. Cuando la recta pasa por el origen de coordenadas el valor de b es cero y la
ecuación es de la forma y = mx.

51


La representación gráfica de esta función es:
y
y = m x +b

y=mx
b

m

x

Figura Nº 14: Representación de dos funciones lineales.

Ejemplo 6:
Como se vio en el capítulo de unidades, las escalas de temperatura Centígrada y Fahrenheit
cumplen las siguientes relaciones:
Fusión Ebullición
Hielo Agua
ºC 0 100
ºF 32 212

Tabla Nº 4: Puntos de fusión y ebullición del agua a presión atmosférica.

Si llamamos x a la temperatura °C e y a la temperatura en °F, los puntos ( x;y) que
tenemos para este ejemplo son x1= 0°C e y1=32°F o sea (0;32) y x2= 100°C e y2=212°F o
sea ( 100; 212). Representando gráficamente estos pares ordenados tenemos:

Relación entre escalas termométricas,
Temperatura

250
200
en °F

150
100
50
0
0 20 40 60 80 100 120
Temperatura en °C

Figura Nº 15: ºC vs. ºF.

52


Como vemos, podemos unir estos puntos por medio de una recta, por lo tanto la función
que relaciona estas dos temperaturas es una función lineal de la forma y = mx+b.
Ahora explicaremos como encontrar los valores de m y b para armar la ecuación. Se dijo
que la pendiente daba la inclinación de la recta (la variación en y con respecto a la
variación en x.), esto es:

∆y y 2 − y1 212 − 32
m= = = = 1,8
∆x x 2 − x1 100 − 0

y la ordenada al origen es b =32, ya que es el corte con el eje de las y (o sea cuando x =0).

⇒ y = mx +b ∴ y = 1,8 x + 32 ∴ °F = 1,8 °C + 32

La utilidad de esta expresión es que podemos obtener el valor de la temperatura en °F
para cualquier valor de temperatura en °C.

5.7- LA FUNCIÓN CUADRÁTICA

Analice el siguiente ejemplo:
Se necesita averiguar el área de un corral cuadrado sabiendo que tiene 2 metros de
cada lado.
La solución es inmediata:
Área = lado por lado ⇒ A= l l = l2 ⇒ A1 = 22 = 4, ¿Y si tuviera 3m de lado? ¿4m de lado?,
etc.
En este caso se podría calcular:
A2 = 32 =9
A3 = 42 = 16
Si se analizan los resultados obtenidos se podría pensar que ahora, para cualquier medida
del corral tendríamos:
y = x2
graficando los datos del ejemplo:
Area del corral (m 2)

30
25
20
15
10
5
0
0 1 2 3 4 5 6
Longitud de cada lado (m)

Figura Nº 16: Área del corral vs. longitud del lado.

53


Evidentemente, a estos puntos ya no los podemos unir con una recta, la línea que los une
tendrá una forma particular llamada “parábola” que es la representación gráfica de la
función cuadrática.

Definición:
Una función f (x) es una función cuadrática si y solo si, se puede expresar en la forma:

f(x) = ax2+bx+c , en donde a, b y c son constantes y a ≠ o

La gráfica de una función cuadrática queda determinada por los valores que toman los
parámetros (a, b y c) y es simétrica respecto de un eje llamado “eje de simetría”.

Vamos a analizar ahora como es dicha gráfica con respecto a cada uno de los parámetros:

Primer caso: análisis del parámetro “a”
Si consideramos la función y = x2, con unos pocos valores obtenidos de la tabla, daremos
su gráfica:
x -3 -2 -1 0 1 2 3
2
y=x 9 4 1 0 1 4 9

Tabla Nº 6: Efecto del parámetro “a” para y= x2.

10
8
6
y

4
a=1
2
0
-4 -3 -2 -1 0 1 2 3 4
x

Figura Nº 17: Gráfico de la función y=x2.

Si ahora consideramos y = 2 x2, tenemos:

x -3 -2 -1 0 1 2 3
y = 2 x2 18 8 2 0 2 8 18

Tabla Nº 7: Efecto del parámetro “a” para y= 2x2.

54


20
15
10
y
a=2
5
0
-4 -3 -2 -1 0 1 2 3 4
x

Figura Nº 18: Gráfico de la función y=2x2.

Por último podríamos considerar y = -2 x2 en cuyo caso el gráfico sería:

20

10
a=-2
0
y

-4 -3 -2 -1 0 1 2 3 4
-10

-20
x

Figura Nº 19: Gráfico de la función y=-2x2.

Si ahora superponemos las tres gráficas obtenemos:

20
a=2
10
a=1
0
y

-4 -3 -2 -1 0 1 2 3 4
-10
a=-2
-20
x

Figura Nº 20: Gráfico de las funciones y=x2, y=2 x2 e y =-2 x2.

55


Vemos que:

a) Si a >0 , la parábola tiene ramas hacia arriba y la función y = ax2 toma el menor valor
(valor mínimo) en el origen.
b) Si a < 0 , la parábola tiene ramas hacia abajo y la función toma el mayor valor ( valor
máximo) en el origen.
Estos mínimos y máximos se toman sobre el “eje de simetría” de la parábola (de ecuación
x = 0) en un punto llamado vértice.
c) El coeficiente del término cuadrático “ a”, produce:

Cierre de las ramas de la parábola hacia el eje y , si

⎜a ⎢> 1 por ejemplo si: a > 1 ⇒ a x2 > x2 y si a < -1 ⇒ a x2 < - x2

Apertura de las ramas hacia el eje x, si

⎜a ⎢< 1 por ejemplo si: 0 < a < 1 ⇒ a x2 > x2 y si -1 < a < 0
⇒ -x2 < a x2 < 0

Segundo caso: análisis del parámetro “c”.

Si consideramos la función y = ax2+c, vemos que el valor de y se obtiene sumándole c al
valor obtenido por la función y = ax2, lo que produce un desplazamiento de esta parábola en
sentido vertical, hacia arriba o hacia abajo según si c > 0 ó c< 0.

30
20 y=2x 2+10
y=2 x 2
10
y

0
-4 -3 -2 -1 -10 0 1 2 3 4
y=2x 2-10
-20
x

Figura Nº 21: Efecto del parámetro “c”.

Realiza el gráfico de la función cuadrática y = ax2+c Si a < 0 y c >0 y si a< 0 y
c <0

56


Tercer caso: analizamos el parámetro “b”.

Hasta ahora en las ecuaciones consideradas no hay término lineal o sea que b = 0 y el eje de
simetría de la parábola coincide con el eje y. Nos preguntamos ahora ¿Qué sucede si el
parámetro b ≠ 0 ?
Consideremos la siguiente función: y = x2 -2 x, graficándola tendríamos:

4
3
2
y=x 2-2 x
1
y

b=-2
0
-4 -3 -2 -1 -1 0 1 2 3 4
-2
x

Figura Nº 22: Efecto del parámetro “b”.

En este caso el eje de simetría no es el eje y.
En el gráfico anterior vemos que el vértice se encuentra en el punto de coordenadas (1;-1).
Así es que nos interesa encontrar cuál es la ecuación de la parábola con vértice en ( xv;yv)
y eje de simetría distinto del eje y.

Por medio del planteo de ecuaciones matemáticas, que no desarrollaremos, se llega a que
una parábola cuya función cuadrática es y = ax2+bx+c, tiene por coordenadas del vértice
los siguientes valores:
b
xv = −
2a

2 b 2 4ac − b 2
y v = c − axv = c − =
4a 4a

Para la última función considerada, y = x2 -2 x, existen dos valores de x para los cuales la
función toma el valor cero o sea y = 0, estos puntos (0 y 2) son los puntos de corte de la
parábola con el eje de las x.
Que la parábola y = ax2+bx+c corte al eje x significa que existen valores de x que hacen
que la ecuación se iguale a cero, es decir:
a x2 + b x + c =0
esto se expresa diciendo que los valores de x son la solución a dicha ecuación de segundo
grado.
La fórmula para el cálculo de los valores de x que hacen que y = 0 viene dada por:

57


− b ± b 2 − 4ac
x=
2a
a través de ésta obtenemos los de x1 y x2 que son los puntos de corte de la parábola con el
eje de las abscisas.
Es interesante analizar por donde va a pasar la parábola mirando solamente los valores que
toma el discriminante (llamamos discriminante a ∆ = b 2 − 4ac ):
1) Si el discriminante > 0, la parábola corta al eje x en dos puntos.
2) Si el discriminante = 0, la parábola corta al eje x en un solo punto.
3) Si el discriminante < 0, la parábola no corta al eje x.

La utilidad que tienen todas estas herramientas es que se puede analizar la forma que tendrá
una función cuadrática cualquiera y graficarla solamente con estos puntos particulares que
hemos visto, sin necesidad de realizar punto a punto la tabla correspondiente.

Ejemplo 7
Dada la siguiente función cuadrática:

y = x2-2x+2
Calcular:

1) ¿Hacia donde van las ramas de la parábola?
2) ¿Dónde está el vértice de la parábola?
3) ¿Cuál es el corte con el eje x?
4) ¿Cuál es el corte con el eje y?
5) ¿La parábola alcanza un valor máximo ó un mínimo?

Solución:

1) En esta parábola , tenemos que:
a = 1 ; b =-2 ; c =2

Como a >0, la parábola tiene ramas hacia arriba.

− (− 2 )
y v = (1) − 2(1) + 2 = 1
2
2) x v = =1 y
2 ×1

3) Para saber cuando la parábola corta al eje x, entonces y =0 calculamos:

− (− 2 ) ± (− 2)2 − 4 ⋅ 1 ⋅ 2 2± −4
x= =
2 ⋅1 2

58


vemos que el discriminante es menor que cero, por lo tanto la parábola nunca corta al eje x.

4) De la misma manera que el inciso anterior, para determinar cuando la parábola corta al
eje y, entonces x=0, y de la ecuación:

y = 0-0+2 =2

Como la parábola tiene ramas que abren hacia arriba, entonces ésta tiene un mínimo. El
valor mínimo es yv =1
Con todos estos puntos ahora estamos en condiciones de ver la forma aproximada que
tendrá el gráfico de la parábola.

15
Eje de simetría
10
y

5
y=x2-2 x+2
0
-3 -2 -1 0 1 2 3 4 5
x

Figura Nº 23: Gráfico ejemplo Nº 7.

5.8- EJERCICIOS DE APLICACION

Función lineal

Ejercicio N°1:
¿Cuál es la función que relaciona los litros de leche diarios producidos en función del
número de vacas del establecimiento, teniendo presente la siguiente tabla de datos:

Cantidad promedio de leche diaria
Nº de vacas
(lt/día)
150 3.000
200 4.000
250 5.000
300 6.000

Tabla Nº 5: Cantidad de leche obtenida vs. cantidad de vacas.

59


Ejercicio N° 2:
Grafique cada una de las siguientes rectas, decir además cuál es la pendiente y cuál es la
ordenada en el origen.
a) y = 5x – 2
b) y = 2x
c) 2y = -6x + 2
d) y = 3

Ejercicio N° 3:
La energía del alimento consumido por un animal es el factor determinante para el tiempo de
sobrevivencia en inedia grave, pero bajo ciertas condiciones el calor puede prolongar la
vida en la inedia.
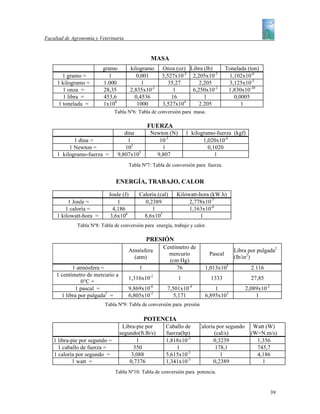
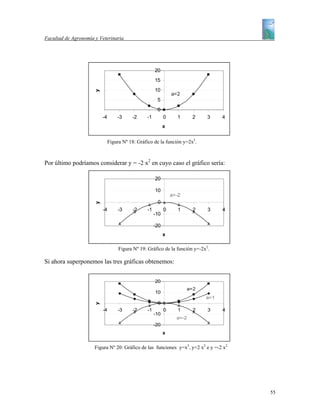
La siguiente figura muestra el efecto de la temperatura ambiente en el tiempo de sobrevivencia
en ratas en inedia grave (con agua solamente) a la edad aproximada de 100 días.
16
sobrevida (días)

14
Tiempo de

12
10
8
6
4
2
0
15 20 25 30 35 40

Temperatura ambiente (°C)

Figura Nº 15: Tiempo de sobrevida vs. Temperatura ambiente.
a) ¿Cuál es la ecuación que relaciona el tiempo de sobrevivencia en función de la
temperatura ambiente en el intervalo [20;30] ?
b) Si el objetivo es prolongar la vida del animal ¿Convendrá aumentar la temperatura de
30 °C hasta 35 °C? ¿Por qué?

Ejercicio N° 4:
El aire mantenido en la cavidad bucal de la anguila eléctrica pierde O2 oxígeno gradualmente según
éste va siendo utilizado por el pez.
La siguiente tabla muestra los valores obtenidos de la presión parcial de O2 medida en mm Hg
(PO2) para diferentes valores del tiempo entre respiraciones en segundos (t) durante la realización de
un experimento:

PO 2 t Encontrar la ecuación para la
presión parcial de oxígeno en
110 10 función del tiempo entre
100 20 respiraciones.
90 30
80 40
70 50
Tabla Nº 6: Presión parcial de oxigeno vs. tiempo.

60


Función cuadrática
Ejercicio Nº 5:
Graficar cada una de las siguientes funciones cuadráticas indicando el valor de “a”,”b” y
“c”, decir además si poseen un valor máximo o un valor mínimo y dar ese valor: y = x 2 − 3
a) y = ( x − 3) 2 + 2 c) y = x 2 + 8 x e) y = − x 2
b) y = x 2 − 3x + 7 d) y = −4 x 2 + x − 6

Ejercicio Nº 6:
En un medio caliente, la temperatura del cuerpo de un animal puede aumentar, pero seguir
regulándose a este nivel superior. Este fenómeno se denomina hipertermia controlada.
Cuando se introdujeron cerdos en un recinto con la temperatura del aire de 32,2 °C su
temperatura corporal desde los 120 minutos hasta los 210 minutos evolucionó según la
siguiente función:

Te = 0,0003 ti2 - 0,0912 ti + 30,788
donde:
Te = Temperatura rectal (°C)
ti = Tiempo de exposición (min.).

Obtener la grafica de dicha función.

Ejercicio Nº 7:
La siguiente gráfica muestra la evolución de la contracción isotónica del músculo sartorius
del sapo Bufo marinus. Obtenga los datos necesarios de manera tal que le permita escribir
la ecuación cuadrática que ajuste tales datos.

Contracción isotónica del músculo Sartorius del
sapo Bufo marinus.
acortamiento (cm)

1
Distancia de

0,8
0,6
0,4
0,2
0
0 10 20 30 40 50 60 70 80 90
Fuerza (g)

Figura Nº 24: Distancia de acortamiento muscular vs. fuerza aplicada.

61


BIBLIOGRAFÍA:

Matemática 1 – COU; Autores: J. M. Martinez-Mediano, Cuadra López Rafael,
Jiménez Villanueva J.L.; Editorial: Mc Graw-Hill, Año 1996.
Matemática 2 – COU; Autores: Fernado Garjo, Delgado Miguel, Tabuenca Jaime;
Editorial: Mc Graw-Hill, Año 1995.
Matemática Básica para las Ciencias de la Vida; Autores: Bocco Mónica; Editorial:
Trianfar, Año 2001.
Matemática para Administración, Economía, Ciencias Sociales y de la Vida;
Autores: Ernest F. Haeussler J.R., Paúl Richard S.; Editorial: Prentice Hall, Año
1997, Octava edición.
Cálculo; Autores: Larson, Hostetler, Edwards; Editorial: Mc Graw-Hill, Año 2001,
Sexta edición, Volumen 1.
Física; Autores: Resnick-Holliday, Kane; Editorial: Cecsa, Año 1997, Cuarta
edición, Volumen 1.

62


63

Matematica Ingreso 2009

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Matematica Ingreso 2009

Último

Matematica Ingreso 2009