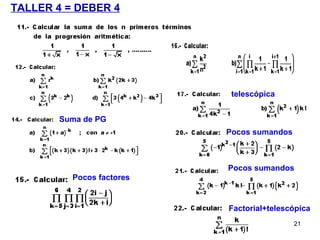
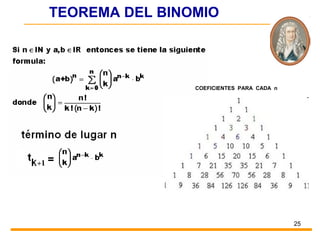
Este documento trata sobre sucesiones matemáticas. Explica que una sucesión es un conjunto de números dispuestos uno después del otro. Define progresiones aritméticas y geométricas, y da ejemplos de sus términos generales y cálculo de sumas parciales. También incluye ejercicios prácticos sobre sucesiones para resolver.

1. MATEMATICAS I Campus Guayaquil MBA-MG. Nelson Córdova

2. SUCESIONES Se llama sucesión a un conjunto de números dispuestos uno a continuación de otro. El término general es a n es un criterio que nos permite determinar cualquier término de la sucesión EJEMPLO 1 : a n = 2n-1 3, 6, 9,..., 3n EJEMPLO 2 : a n = -3n+5 EJEMPLO 3 : a n = n!

3. Sucesiones ( Progresiones) aritméticas (Definición) Una sucesión aritmética (SA) es de la forma El número es el primer término y es la diferencia entre los términos de la sucesión, el término n-ésimo de una sucesión arítmética está dado por Ejemplos : (1) (2) El 11-ésimo término de una SA es 52 y el 19 es 93 , calcular el 1000-ésimo término

4. Sumas parciales en una PA La n-ésima suma parcial de una SA es Se puede calcular de las dos formas siguientes (1) (2) Ejemplos : ¿Cuántos términos de la SA : 5,7,9,…. Hay que sumar para obtener 572? (1) (2)

5. TALLER 1-DEBER 1 NIVEL REPRODUCTIVO 1.- Encuentre el término décimo quinto : 3 , 7 , 11 , 15 , 19 2.- Encuentre la suma 51 + 48 + 45 + 42 +……..+18

6. TALLER 1-DEBER 1 NIVEL TRANSFERENCIAL Determine la suma indicada de las progresiones siguientes: 1.- 1+4+7+10+……..; 30 t érminos 2.- Si los términos tercero y séptimo de una P.A. son 18 y 30 respectivamente . Encuentre La suma hasta el décimo quinto término

7. TALLER 1-DEBER 1 NIVEL CR Í TICO Invente una PA que todos los números sean impares y que la suma sea igual al doble del término central NIVEL CR EATIVO ( Incrementos en los salarios) El salario mensual de Carla se incremento anualmente formando una P.A. . Ella ganó $440 al mes durante el séptimo año y $1160 Al mes durante el vigésimo año : Calcule su salario inicial y su incremento anual Cuál sería su salario de jubilación al completar 38 años de servicio?

8. (Definición) Una sucesión Geométrica (SG) es de la forma El número es el primer término y es la razón entre los términos de la sucesión. El término n-ésimo de una sucesión está dado por Ejemplo : (1) (2) Sucesiones ( Progresiones) Geométricas (3)

9. Respuestas (Definición) La Suma de los primeros n términos de sucesión Geométrica (SG) es de la forma Ejemplos de suma 1 . En una progresión geométrica, se tiene: t1 = 4 y t6 = 972. Determine la suma hasta el 6º término. R : = 1456 2.- Encontrar la suma hasta el 7mo término de la siguiente progresión que cumple con que t 3 = 20 y t 7 = 1620 R : 2,428.88 (1) (2) (3)

10. TALLER 2-DEBER 2 NIVEL REPRODUCTIVO I Encuentre el término específico 1.- El noveno término de la sucesión 3, 6 , 12 , 24 2.- El n-ésimo término de la sucesión II Que lugar ocupa en la sucesión el último término dado? 3.- 96 , 48 , 24 , 12 ,…….., 4.- 18 , 12 , 18 , …………,

11. TALLER 2-DEBER 2 NIVEL CR Í TICO NIVEL CR EATIVO Intercalar tres números entre los números 8 y 128. de manera que se obtenga una PG de 5 términos. (plan de ahorro) Al inicio de cada mes, Jos é deposita $200 en una cuenta de ahorros que gana un interés a una tasa de 0.5% al mes sobre el mínimo balance mensual . Cual es el valor de la inversión después De 2 años ) esto es en 25 depósitos?

12. INDUCCION

13. INDUCCION EJEMPLOS : Demuestre las siguientes igualdades usando Inducción

14. TALLER 3 =DEBER 3

15. INDUCCION EJERCICIOS DE DIVISIBILIDAD EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 1

16. TALLER 3B = DEBER 3B 1.- 2.- 3.- 4.- 5.-

17. SUMATORIAS Notación Sigma Dada la sucesión se puede representar con la notación sigma de la siguiente manera: Ejemplos : (1) Calcular las siguientes sumas (i) ( ii ) (2) Expresar en notación sigma (i) (ii)

18. Ejemplos : Calcular (1) (2) (F1) (F2) (F3) (F4) (3) (4) FORMULAS DE LAS SUMATORIAS (F5) p p p p p

19. SUMA DOBLE DOBLE INDICE VARIABLE DIFERENTE CONSTANTE DE POCOS SUMANDOS

20. DEFINIDA POR PARTES

21. TALLER 4 = DEBER 4 Factorial+telescópica Pocos sumandos Pocos sumandos telesc ópica Pocos factores Suma de PG

22. Series infinitas Una serie infinita es una expresión de la forma A una serie infinita de la forma se denomina serie Geométrica Si en una serie geométrica entonces Demostración

23. (1) Determinar (2) (Aplicación-Taller) Ejemplo ¿Cuánto dinero se tiene que invertir ahora al 10% anual, compuesto Anualmente, para proporcionar una anualidad a perpetuidad de 5000 dólares por año ? .El primer pago de 5000 se efectúa ahora.

24. TALLER 5 = Deber 5 a) Calcule la suma infinita: b) 11.- = c) Una pelota siempre rebota de la altura desde la que cae. Si se deja caer desde la altura de 9 pies . ¿ Qué distancia recorre hasta que se para?

25. TEOREMA DEL BINOMIO COEFICIENTES PARA CADA n

26. TEOREMA DEL BINOMIO

28. TALLER 6 = DEBER 6

29. Principios de Conteo (1)

30. (2) (3)

31. Permutaciones Una permutación de un conjunto de objetos distintos , es un ordenamiento de esos objetos Ejemplo1 : Tome las letras de la palabra CUADERNO y encuentre cuantas palabras distintas se pueden formar con esas letras La cantidad de permutaciones de n objetos es ¿Cuántas permutaciones se pueden realizar con 5 letras de la palabra CUADERNO ?

32. En general si un conjunto tiene n elementos, el número de maneras de ordenar r de ellos es Así en el ejemplo anterior :

33. Ejemplo 2 Ejemplo 3

34. El número de permutaciones de n objetos con repetidos es Ejemplos : (1) Determine cuantas palabras diferentes se pueden formar con las letras de la palabra PARALELEPIPEDO (2) Determine el número de formas distintas de colocar en fila 15 bolas en una fila, si 4 son rojas 3, son amarillas ,6 son negras y 2 son azules

35. TALLER 7 = DEBER 7

36. COMBINACIONES

37. Ejemplo 1 : Ejemplo 2 :

38. Ejemplo 3: Ejemplo 4 :

39. TALLER 8 = DEBER 8 1.- Un estudiante recibe una lista de lectura de 10 libros, de los cuales debe elegir dos para su lectura ¿ De cuántas formas puede hacerse la elección? 2.- Un estudiante presenta un examen donde debe contestar 10 de 15 preguntas a) ¿De cuantas formas puede elegir las 10 preguntas? b) ¿ de cuantas maneras puede escoger las 10 preguntas , si debe contestar exactamente dos de las tres primeras? 3.-De 7 físicos y 4 matemáticos se va a formar un comité de 6 ¿ de cuantas maneras puede formarse? a) Cuando haya en el comité 2 matemáticos b) Cuando haya como mínimo 2 matemáticos

40. 4.- Una empresa necesita 14 personas para hacer un trabajo, distribuidas de la siguiente manera : 4 mujeres , 5 hombres y los restantes pueden ser de uno u otro sexo. De cuantas maneras puede elegir la empresa las 14 personas si hay 18 candidatos de los cuales 8 son mujeres y 10 son hombres. 5.- Cu ántas combinaciones diferentes pueden formarse tomando cuatro de los dígitos 3 , 4 , 7, 5 , 8 ,1 6. Se desea dividir un curso de 40 alumnos en 4 grupos ; de 8; 9; 11; 12 alumnos respectivamente de modo que los alumnos ANA , BERNARDO, CARLOS, Y DELIA queden en un grupo diferente . De cuantas maneras puede hacerse ?