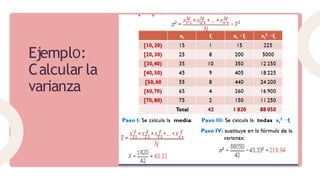
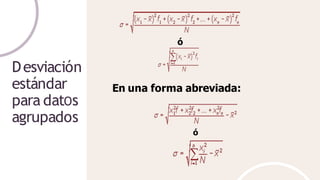
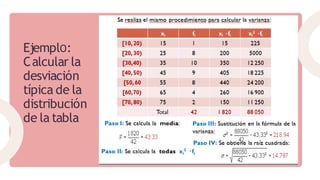
Este documento describe diferentes medidas de dispersión estadísticas como la desviación media, varianza, desviación estándar y coeficiente de variación. Explica las fórmulas para calcular cada medida y sus propiedades. También incluye ejemplos numéricos para ilustrar cómo calcular estas medidas a partir de conjuntos de datos.

1. UNIDAD V.
MEDIDAS DE
DESVIACIÓN
ANALISIS DE DATOS ESTADISTICOS Y USO DE LAS
TIC´S
E.E. Lizette Gonzalez Guarello

2. Desviación media.
La desviación media es
la media de los valores
absolutos
de la diferencia de cada valor de
la distribución con la media
aritmética.
La desviación media es igual o
menor que la desviación
estándar :
Fórmulaparadatos
no agrupados:
Fórmulapara
datos agrupados:

3. EjemplO En el paso 1 se ha obtenido la media ,
después la columna con las diferencias y a la
derecha,las diferencias en valor absoluto.
Finalmente, en el paso 2, aplicamos
la fórmulade ladesviación
media:
Se verifica aquí que la desviación
media nuncasuperaaladesviación
estándar:

4. Varianza
La varianza es la
media aritmética del
cuadrado de las
desviaciones respecto
a la media de una
distribución
estadística.
La varianza se
representa por σ2. La
fórmulaestádadapor:
paradatosno agrupados:
ó
Enunaformaabreviada:
ó

5. EjemplO
CALCULAR LAVARIANZA DE LADISTRIBUCIÓN
9, 3, 8, 8, 9, 8, 9, 18
Paso I: Se calculala media:
Paso II: Sustituimosen lafórmulade lavarianza:

6. EjemplO:
Calcular la
varianza

7. Propiedades de la varianza
1.La varianza será siempre un valor positivo o cero, en
el caso de que laspuntuaciones sean iguales.
2.Si atodos los valores de la variable se les suma
un número lavarianzano varía.
3.Si todos los valores de la variable se multiplican por
un número la varianza queda multiplicada por el
cuadrado de dicho número.
4.Si tenemosvariasdistribuciones con lamismamediay
conocemossusrespectivas varianzasse puede calcular
lavarianzatotal.

8. O bservaciones de la varianza
La varianza, al igual que la media, es uníndice muy
sensible alaspuntuacionesextremas.
vEn los casos que no se puede hallar la media
tampoco seráposible hallar lavarianza.
vLavarianzano viene expresadaen lasmismas
unidadesque los datos, ya que las desviaciones
están elevadasal cuadrado.

9. Desviación Estándar
La desviación estándar o
desviación típica es la
raíz cuadrada de la
varianza. Es decir, la raíz
cuadrada de la media de
los cuadrados de las
puntuaciones de
desviación.
La desviación estándar
se representa por σ. La
fórmulaestádadapor:
paradatos no agrupados:
ó
En unaformaabreviada:
ó

10. Desviación
estándar
para datOs
agrupados
En una forma abreviada:
ó
ó

11. EjemplO
CALCULAR LA DESVIACIÓN ESTÁNDAR DE LA DISTRIBUCIÓN:
9,3,8,8,9,8,9,18
Paso I: Se calculala media:
Paso II: Sustituimos en la fórmulade la desviación estandar:

12. EjemplO:
Calcular la
desviación
típica de la
distribución
de la tabla

13. Propiedades de la desviación estándar
1.La desviación estándar será siempre un valor positivo
o cero, en el caso de que las puntuaciones sean
iguales.
2.Si atodos los valores de la variable se les suma
un número la desviación estándar no varía.
3.Si todos los valores de la variable se multiplican por
un número la desviación estándar queda multiplicada
por dicho número.
4.Si tenemosvariasdistribuciones con lamismamedia
y conocemos sus respectivas desviaciones estándar
se puede calcular la desviación estándar total.

14. Observaciones de la desviación estándar
Ladesviación estándar,al igual que lamediay la
varianza,esun índice muy sensible alas
puntuacionesextremas.
En loscasosque no se puede hallar lamedia
tampoco seráposible hallar la desviación estándar.
Cuanta máspequeña sea la desviación estándar
mayorserálaconcentración de datosalrededor de
lamedia.

15. COeficiente de variación
Es unamedidade la dispersión relativa de un conjunto de datos, que se
obtiene dividiendo la desviación estándar del conjunto entre su media
aritméticay se expresageneralmente en términosporcentuales.
Esunamedidaque se empleafundamentalmente para:
Comparar la variabilidad entre dos grupos de datos referidos a
distintos sistemas de unidades de medida.Por ejemplo, kilogramosy
centímetros.
Comparar la variabilidad entre dos gruposde datos obtenidos por
doso máspersonas distintas.
Comparar dosgruposde datosque tienen distintamedia.
Determinar si cierta mediaes consistente con cierta varianza.

16. COeficiente de variación
EL COEFICIENTE DE VARIACIÓN ES LA RELACIÓN ENTRE LA
DESVIACIÓN TÍPICA DE UNA M UESTRA Y SU M EDIA.
El coeficiente de variación se suele expresar en porcentajes:
El coeficiente de variación permite comparar las dispersiones de
dos distribuciones distintas, siempre que sus medias sean
positivas.