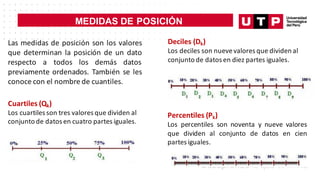
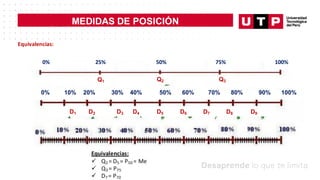
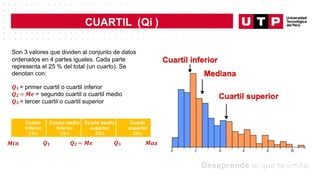
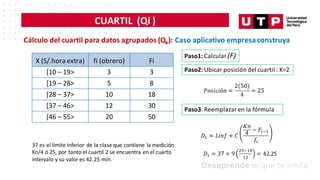
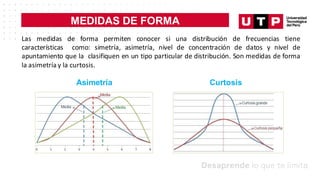
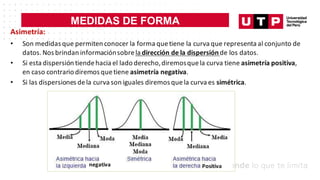
Este documento trata sobre medidas de posición y probabilidades. En la sesión, el estudiante aprende sobre medidas de posición como cuartiles, deciles y percentiles, y cómo calcular e interpretar estas medidas para un conjunto de datos. El objetivo de la sesión es que el estudiante sea capaz de calcular e interpretar medidas de posición y de forma para analizar un conjunto de datos.

1. SESIÓN 6
ESTADÍSTICA DESCRIPTIVA
Y PROBABILIDADES

2. MEDIDAS DE POSICIÓN Y
FORMA

3. Las medidas de posición, son bastante útiles, porque
permiten dividir a conjunto de datos o muestra en partes
iguales. Se utilizan para clasificar a un individuo o elemento
dentro de dicha muestra o población. Ejemplos: el peso de
las personas tomando en cuenta su edad, al momento de
caminar en línea recta, al lanzar una pelota de baloncesto,
etc.

4. Al finalizar la sesión de clase, el
estudiante calcula e interpreta
las medidas de posición y de
forma para un conjunto de datos.
LOGRO DE LA SESIÓN

5. Las medidas de posición, son bastante útiles, porque
permiten dividir a conjunto de datos o muestra en partes
iguales. Se utilizan para clasificar a un individuo o elemento
dentro de dicha muestra o población. Ejemplos: el peso de
las personas tomando en cuenta su edad, al momento de
caminar en línea recta, al lanzar una pelota de baloncesto,
etc.

6. MEDIDAS DE
POSICIÓN
MEDIDAS DE FORMA:
ASIMETRÍA Y
CURTOSIS
TEMARIO

7. MEDIDAS DE POSICIÓN
Si el peso del bebé es inferior al percentil
10 para su edad gestacional (lo que
significa que el 90% de los bebés de la
misma edad gestacional pesan más), al
bebé también se le denomina "pequeño
para su edad gestacional".

8. MEDIDAS DE POSICIÓN
Las medidas de posición son los valores
que determinan la posición de un dato
respecto a todos los demás datos
previamente ordenados. También se les
conoce con el nombre de cuantiles.
Cuartiles (Qk)
Los cuartiles son tres valores que dividen al
conjunto de datos en cuatro partes iguales.
Deciles (Dk)
Los deciles son nuevevalores que dividen al
conjunto de datos en diez partes iguales.
Percentiles (Pk)
Los percentiles son noventa y nueve valores
que dividen al conjunto de datos en cien
partes iguales.

9. MEDIDAS DE POSICIÓN
Equivalencias:
0% 25% 50% 75% 100%
Q1 Q2 Q3
0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
D1 D2 D3 D4 D5 D6 D7 D8 D9
Equivalencias:
ü Q2 = D5 = P50 = Me
ü Q3 = P75
ü D7 = P70

10. PERCENTIL
Son 99 valores que dividen al conjunto de datos
ordenados en 100 partes iguales. Cada parte
representa el 1 % del total. Se denotan con:
𝑷𝟏 = primer percentil
𝑷𝟐𝟓 = 𝑸𝟏 = percentil 25
𝑷𝟓𝟎 = 𝑸𝟐 = 𝑴𝒆 = percentil 50
𝑷𝟕𝟓 = 𝑸𝟑 = percentil 75
𝑷𝟗𝟗 = percentil 99
1% 𝟏% … … … … 𝟏% 𝟏%
𝑴𝒊𝒏 𝑷𝟏 𝑷𝟐 𝑷𝟓𝟎 𝑷𝟗𝟖 𝑷𝟗𝟗 𝑴𝒂𝒙
si el puntaje alcanzado es 19, entonces se encuentra en el percentil
67, esto significa que este examinado está mejor posicionado que el
66% de los examinados

11. PERCENTIL (Pi)
𝑥
Cálculo de percentiles para datos no agrupados (Pk)
Procedimiento a seguir:
1. Ordenar los datos en
forma ascendente
2. Calcular la posición del
percentil k-ésimo mediante
la siguienteexpresión:
Posición = k (n + 1)
100
3. Ubicar el percentil buscado en
la posición calculada si éste es
un número entero, de lo
contrario dicho valor se calcula
en forma proporcional en base a
la siguientefórmula:
Pk = Li + partedecimalx (Ld– Li)
Donde:
Pk: Percentil k-ésimo.
Li: Valor del dato ubicado en la posición con el valor de k aproximado a entero.
Ld: Valor del dato superior o inmediato a Li

12. PERCENTIL
𝑥
Cálculo de percentiles para datos no agrupados (Pk)
Caso: Duración de una batería
Un fabricante de componentes electrónicos se interesa en determinar el tiempo de vida útil
de cierto tipo de batería. Se presenta a continuación una muestra de 24 horas de vida
registradas:
134 122 122 125 126 172 131 180
134 120 136 161 140 140 140 145
146 153 155 159 139 162 128 132
¿Cuál es el valor a partir del cuál se encuentra el 30% superior de los tiempos en
horasde vida útil de las baterías?

13. PERCENTIL
Cálculo de percentilespara datosno agrupados(Pk)
Caso: Duración de una batería
Solución
1. Ordenando los datos en forma ascendente
120 122 122 125 126 128 131 132
134 134 136 139 140 140 140 145
146 153 155 159 161 162 172 180
n=24
2. Cálculo de la posición del percentil70: (k=70)
Posición = 70 (24+1) =17.5
100
Pidenhallar:
Posición = 17.5
Nota:Partedecimal=0.5

14. PERCENTIL
Cálculo de percentilespara datosno agrupados(Pk)
El valor de 17.5 se encuentra entre las posiciones 17 y 18 de los datos ordenados en forma ascendente:
X17 = 146, entonces:Li =146
X18 = 153, entonces:Ld =153
3. Cálculo de P70:
Pk = Li + partedecimal x (Ld – Li) P70 = 146
+ 0.5 x (153 – 146)
P70 = 149.5 horas
120 122 122 125 126 128 131 132
134 134 136 139 140 140 140 145
146 153 155 159 161 162 172 180
Interpretación:
El 70% de los tiempos de vida útil registrados son
menores iguales a 149.5 horas.

15. PERCENTIL
Caso: Tiempo de espera de clientes
Solución
Se presentan los tiempos de espera (en
minutos) de 11 clientes para ser atendidos en la
ventanilla de un banco:
1. Ordenando los datos en forma ascendente
𝒙𝟏 𝒙𝟐 𝒙𝟑 𝒙𝟒 𝒙𝟓 𝒙𝟔 𝒙𝟕 𝒙𝟖 𝒙𝟗 𝒙𝟏𝟎 𝒙𝟏𝟏
15 10 20 13 8 15 9 12 18 11 14
𝒙𝟏 𝒙𝟐 𝒙𝟑 𝒙𝟒 𝒙𝟓 𝒙𝟔 𝒙𝟕 𝒙𝟖 𝒙𝟗 𝒙𝟏𝟎 𝒙𝟏𝟏
8 9 10 11 12 13 14 15 15 18 20
3. Cálculo de P30:
2. Cálculo de la posición del percentil30: (k=30)
Pk = Li + partedecimal x (Ld – Li) P70 = 10 +
0.6 x (11 – 10)
P70 = 10.6 minutos

16. PERCENTIL
Cálculo de percentilespara datosagrupados (Pk)
Procedimiento a seguir:
Paso1: Calcular frecuencia absoluta acumulada (F)
Paso2: Ubicar posición del percentil
Paso3: Reemplazar en la fórmula
Recuerda!
Donde:
k: Valor k-ésimo según el cuantil Ck: k-ésimo valor del cuantil.
Li: Límiteinferior del intervalo donde se encuentra el valor del cuantil Ck:
c: Amplitud dela clase
Fi-1: Frecuencia acumulada.
fi: Frecuencia absoluta del intervalo donde se encuentra el valor del cuantil Ck:

17. PERCENTIL
Cálculo de percentiles para datos agrupados (Pk): Caso aplicativo
Si se ha registrado en el siguientecuadro los pagos adicionales (soles) por concepto de horas
extras duranteuna semana de todos los trabajadores deuna empresa constructora
X (S/.hora extra) fi (obrero)
[50 – 70> 30
[70 – 90> 50
[90 – 110> 65
[110 – 130> 30
[130 – 150> 25
¿Cuál es el valor a partir del cuál se encuentra el 55% de los obreros con
menores o inferiores montos por horas extras en semana?

18. PERCENTIL
Cálculo de percentiles para datos agrupados (Pk): Caso aplicativo empresa construya
X (S/.hora extra) fi (obrero) Fi
[50 – 70> 30 30
[70 – 90> 50
[90 – 110>
[110 – 130> 30 175
[130 – 150> 25 200
Para el 55% inferior de los datos correspondek = 55.
Paso1: Calcular (F)
Paso2: Ubicar posición del percentil : K=55
Paso3: Reemplazar en la fórmula
el 55% de los obreros tienen un tiempo de extra menor a 99.23 soles
Y el otro 45% de los obreros tiene un tiempo extra mayor a 45%

19. PERCENTIL
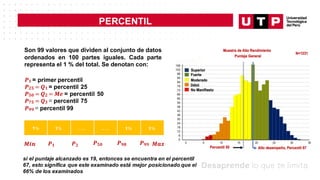
Cálculo de percentiles para datos agrupados (Pk): Caso aplicativo en Android
La empresa SYSTEM S.A.C. se dedica al desarrollo de aplicativos desarrollados en ANDROID para
dispositivos móviles. A la empresa le interesa desarrollar aplicaciones de calidad que tengan el menor
tamaño en MB posible para que los usuarios puedan hacer las descarga más rápidamente en sus
dispositivos móviles. A continuación se presentan los tamaños registrados en MB de 40 aplicaciones
desarrolladas:
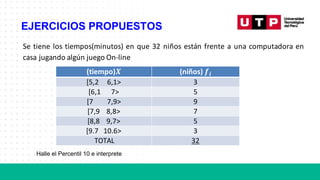
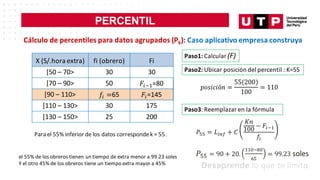
Tamañodel aplicativo (MB) N° de aplicativos
[0; 10> 8
[10; 20> 12
[20; 30> 7
[30; 40> 10
[40; 50] 3
Total 40
El área de calidad de software de la empresa indicó que si el promedio del tamaño registrado de las
aplicaciones desarrolladas pertenece al 45% inferior de los datos, se le dará un bono a los programadores
a fin de mes. ¿Cuál es la decisión final que tomará el gerentede la empresa?

20. PERCENTIL
Cálculo de percentiles para datos agrupados (Pk): Caso aplicativo en Android
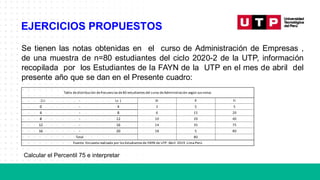
Solución:
1. Cálculo de la marca de clase y de la media: (condición delgerente)
Tamañodel aplicativo
(MB)
N° de
aplicativos (fi)
Marca de
clase (Xi)
Xi. fi
[0; 10> 8 5 40
[10; 20> 12 15 180
[20; 30> 7 25 175
[30; 40> 10 35 350
[40; 50] 3 45 135
Total 40 880
+
𝑋
9 =
∑𝑋;𝑓;
𝑛
=
880
40
= 22 𝑀𝑏

21. PERCENTIL
Cálculo de percentiles para datos agrupados (Pk): Caso aplicativo en Android
Solución:
2. Cálculo de la posición del percentil:(k=45)
Tamañodel aplicativo
(MB)
N° de
aplicativos (fi)
Frecuencia
acumulada (Fi)
[0; 10> 8 8
[10; 20> 12 20
[20; 30> 7 27
[30; 40> 10 37
[40; 50] 3 40
Total n=40
Para el45% inferior de los datos correspondek =45.
Paso1: Calcular (F)
Paso2: Ubicar posición del percentil :K=45
𝑘 𝑖𝑛
𝑓
𝑃 = 𝐿 + 𝐶
𝐾𝑛
100 − 𝐹𝑖−1
𝑓𝑖
Paso3: Reemplazar en la fórmula
100
45(40)
𝑝𝑜𝑠𝑖𝑐𝑖ó𝑛 = = 18

22. PERCENTIL
Tamaño del aplicativo
(MB)
N° de
aplicativos (fi)
Frecuencia
acumulada (Fi)
[0; 10> 8 Fi-1 = 8
[10; 20> fi = 12 Fi = 20
[20; 30> 7 27
[30; 40> 10 37
[40; 50] 3 40
Total n=40
45
𝑃 = 10 + 10
18 − 8
12
Cálculo de percentiles para datos agrupados (Pk): Caso: Aplicativosen Android
Ubicamos la posición calculada (Posición = 18) en la columna de frecuencias acumuladas(Fi).
Reemplazando
𝑃45 = 18.3 MB
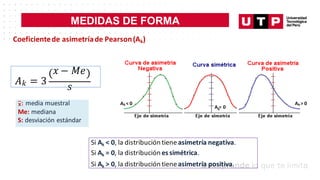
Conclusión: Como el valor de la media ( 𝑋 = 22 MB) es mayor que el valor de P45= 18.3 MB,
no se entregará el bono a los programadores a fin de mes; teniendo en cuenta las
indicaciones del área de calidad del software de la empresa.

23. DECIL (Di )
Son valores que dividen al conjunto en diez
partes iguales son los deciles y se denotan
𝑫𝟏, 𝑫𝟐, 𝑫𝟑, … , 𝑫𝟗
𝑫𝟓 =𝑴𝒆 = quinto decil o decil medio
El histograma muestra la distribución de calificaciones en una
prueba (de 60 puntos) que intentaron 600 estudiantes. El puntaje
de cada alumno está representada por un cuadrado en el
histograma.
El primer decil es 17.5, por lo que la décima parte más débil
de los estudiantes en la clase tenía una marca debajo de esto.
Por lo tanto, este decil resume el desempeño de los
estudiantes más débiles.
Se dice que los estudiantes con calificaciones inferiores a 17.5
están en el decil 1. Aquellos con calificaciones entre 17.5 y 26.5
están en el decil 2, y así sucesivamente, hasta los estudiantes con
calificaciones superiores a 54.5 que están en el decil 10.

24. DECIL (Di )
Cálculo del decil para datosagrupados (Dk)
Procedimiento a seguir:
Paso1: Calcular frecuencia absoluta acumulada (F)
Paso2: Ubicar posición del Decil
Paso3: Reemplazar en la fórmula
Recuerda!
Donde:
k: Valor k-ésimo según el decil Dk: k-ésimo valor del decil.
Li: Límiteinferior del intervalo donde se encuentra el valor del decil Dk:
c: Amplitud dela clase
Fi-1: Frecuencia acumulada.
fi: Frecuencia absoluta del intervalo donde se encuentra el valor del decil Dk:
Ubicar la posición calculada en los
valores de la frecuencia acumulada
Fi. (Se sigue el mismo procedimiento
que el percentil)

25. Cálculo de deciles con datos agrupados
𝑫𝒌 = 𝑳𝒊 + 𝑪
𝒌𝒏 − 𝑭𝒊0𝟏
𝟏𝟎
𝒇𝒊
, 𝒌 = 𝟏,𝟐, …, 𝟗
Ejemplo:
Paralos salarios de 65 empleados de la empresa P&R
determinar e interpretar 𝑫𝟑
Cuadro 1. Salarios de empleados de P&R
𝑺𝒂𝒍𝒂𝒓𝒊𝒐𝒔 𝒇𝒊 𝑭𝒊
[𝟐𝟓𝟎; 𝟐𝟔𝟎 > 8 8
[𝟐𝟔𝟎; 𝟐𝟕𝟎 > 10 18
[𝟐𝟕𝟎; 𝟐𝟖𝟎 > 16 34
[𝟐𝟖𝟎; 𝟐𝟗𝟎 > 14 48
[𝟐𝟗𝟎; 𝟑𝟎𝟎 > 10 58
[𝟑𝟎𝟎; 𝟑𝟏𝟎 > 5 63
[𝟑𝟏𝟎; 𝟑𝟐𝟎 > 2 65
𝑫𝟑 =𝟐𝟕𝟎 + 𝟏𝟎
𝟑×𝟔𝟓 − 𝟏𝟖
𝟏𝟎
𝟏𝟔
⇒ 𝑫𝟑 =𝟐𝟕𝟎. 𝟗𝟒
𝟏𝟎 𝟏𝟎 𝟑
𝒌𝒏
=
𝟑×𝟔𝟓
= 𝟏𝟗. 𝟓 ⇒ 𝑭 = 𝟑𝟒 > 𝟏𝟗. 𝟓
El 3𝟎% de los empleados tiene un salario inferior a
$ 270.94
El 7𝟎% de los empleados tiene un salario superior a
$ 270.94
DECIL (Di )

26. DECIL (Di )
Cálculo del deciles para datos agrupados (Dk): Caso aplicativo
La siguiente tabla muestra el tiempo requerido para auditor saldos decuentas.
Tiempo de
Auditoria
Número de
Registros
(fi )
[10 – 19> 3
[19 – 28> 5
[28 – 37> 10
[37 – 46> 12
[46 – 55> 20
¿Cuál es el primer decil?

27. DECIL (Di )
Cálculo del deciles para datos agrupados (Pk): Caso aplicativo empresa construya
X (S/.hora extra) fi (obrero) Fi
[10 – 19> 3 3
[19 – 28> 5 8
[28 – 37> 10 18
[37 – 46> 12 30
[46 – 55> 20 50
Paso1: Calcular (F)
Paso2: Ubicar posición del decil : K= 1
Paso3: Reemplazar en la fórmula
19 es el límite inferior de la clase que contiene la medición
Kn/10 ó 5, por tanto el decil 1 se encuentra en el segundo
intervalo y su valor es 22.6 min.

28. Son 3 valores que dividen al conjunto de datos
ordenados en 4 partes iguales. Cada parte
representa el 25 % del total (un cuarto). Se
denotan con:
𝑸𝟏 = primer cuartil o cuartil inferior
𝑸𝟐 = 𝑴𝒆 = segundo cuartil o cuartil medio
𝑸𝟑 = tercer cuartil o cuartil superior
Cuarto
inferior
𝟐𝟓%
Cuarto medio
Inferior
𝟐𝟓%
Cuarto medio
superior
𝟐𝟓%
Cuarto
superior
𝟐𝟓%
𝑴𝒊𝒏 𝑸𝟏 𝑸𝟐 = 𝑴𝒆 𝑸𝟑 𝑴𝒂𝒙
CUARTIL (Qi )

29. CUARTIL (Qi )
Cálculo de cuartiles (Qi) para datos agrupados
Procedimiento a seguir:
Paso1: Calcular frecuencia absoluta acumulada (F)
Paso2: Ubicar posición: según el cuartil
Paso3: Reemplazar en la fórmula
Recuerda:
Ubicar la posición calculada en los
valores de la frecuencia acumulada
Fi. (Se sigue el mismo procedimiento
que el percentil)

30. Cálculo de cuartiles con datos agrupados
𝟐. Para calcular el cuartil 𝑸𝒌
𝑸𝒌 = 𝑳𝒊 + 𝑪 𝟒
𝒌𝒏 − 𝑭𝒊0𝟏
𝒇𝒊
, 𝒌 = 𝟏, 𝟐,𝟑
S𝐞 𝐫𝐞𝐚𝐥𝐢𝐳ó 𝐮𝐧 𝐞𝐬𝐭𝐮𝐝𝐢𝐨 𝐜𝐨𝐧 𝐥𝐚 𝐟𝐢𝐧𝐚𝐥𝐢𝐝𝐚𝐝 𝐝𝐞 𝐜𝐨𝐧𝐨𝐜𝐞𝐫 𝐥𝐚
𝐞𝐝𝐚𝐝 𝐞𝐧 𝐪𝐮𝐞 𝐥𝐨𝐬 𝐭𝐫𝐚𝐛𝐚𝐣𝐚𝐝𝐨𝐫𝐞𝐬 𝐝𝐞 𝐮𝐧 𝐝𝐢𝐬𝐭𝐫𝐢𝐭𝐨 𝐩𝐢𝐝𝐢𝐞𝐫𝐨
𝐧 𝐬𝐮 𝐣𝐮𝐛𝐢𝐥𝐚𝐜𝐢ó𝐧. 𝐂𝐚𝐥𝐜𝐮𝐥𝐚𝐫 𝐞 𝐢𝐧𝐭𝐞𝐫𝐩𝐫𝐞𝐭𝐚𝐫 𝑸𝟑
Ejemplo:
Cuadro 2. Edad de Jubilación
𝑬𝒅𝒂𝒅 𝒇𝒊 𝑭𝒊
[𝟔𝟑; 𝟔𝟖 > 71 71
[𝟔𝟖; 𝟕𝟑 > 162 233
[𝟕𝟑; 𝟕𝟖 > 91 324
[𝟕𝟖; 𝟖𝟑 > 79 403
[𝟖𝟑; 𝟖𝟖 > 47 450
𝑸𝟑 = 𝟕𝟖 + 𝟓
𝟑×𝟒𝟓𝟎 −𝟑𝟐𝟒
𝟒
𝟕𝟗
⇒ 𝑸𝟑 = 𝟕𝟖. 𝟖𝟓
𝒌𝒏 𝟑×𝟒𝟓𝟎
𝟏𝟎
=
𝟒
= 𝟑𝟑𝟕. 𝟓 ⇒ 𝑭𝟒 = 𝟒𝟎𝟑 > 𝟑𝟑𝟕. 𝟓
El 75% de los trabajadores se jubiló con una edad
inferior a 78.85 años
CUARTIL (Qi )

31. CUARTIL (Qi )
Cálculo del cuartil para datos agrupados (Qk): Caso aplicativo
La siguiente tabla muestra el tiempo requerido para auditor saldos decuentas.
Tiempo de
Auditoria
Número de
Registros
(fi )
[10 – 19> 3
[19 – 28> 5
[28 – 37> 10
[37 – 46> 12
[46 – 55> 20
¿Cuál es el segundo cuartil?

32. CUARTIL (Qi )
Cálculo del cuartil para datos agrupados (Qk): Caso aplicativo empresaconstruya
X (S/.hora extra) fi (obrero) Fi
[10 – 19> 3 3
[19 – 28> 5 8
[28 – 37> 10 18
[37 – 46> 12 30
[46 – 55> 20 50
Paso1: Calcular (F)
Paso2: Ubicar posición del cuartil : K=2
Paso3: Reemplazar en la fórmula
37 es el límite inferior de la clase que contiene la medición
Kn/4 ó 25, por tanto el cuartil 2 se encuentra en el cuarto
intervalo y su valor es 42.25 min.

33. MEDIDAS DE FORMA
Las medidas de forma permiten conocer si una distribución de frecuencias tiene
características como: simetría, asimetría, nivel de concentración de datos y nivel de
apuntamiento que la clasifiquen en un tipo particular de distribución. Son medidas de forma
la asimetría y la curtosis.
Asimetría Curtosis

34. MEDIDAS DE FORMA
Asimetría:
• Son medidas que permiten conocer la forma quetiene la curva que representa al conjunto de
datos. Nos brindan informaciónsobrela dirección de la dispersiónde los datos.
• Si esta dispersión tiendehacia el lado derecho,diremosquela curva tiene asimetría positiva,
en caso contrario diremos quetiene asimetría negativa.
• Si las dispersiones dela curva son iguales diremos quela curva es simétrica.
negativa Positiva

35. MEDIDAS DE FORMA
Si Ak < 0, la distribución tieneasimetría negativa.
Si Ak = 0, la distribución essimétrica.
Si Ak > 0, la distribución tieneasimetría positiva.
Coeficientede asimetríade Pearson(Ak)
: media muestral
Me: mediana
S: desviación estándar
Ak < 0 Ak > 0
k
A = 0
𝑥 − 𝑀𝑒
𝐴𝑘 = 3
𝑠

36. MEDIDAS DE FORMA
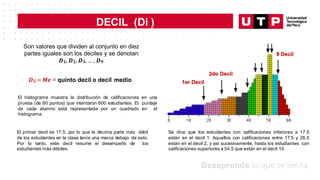
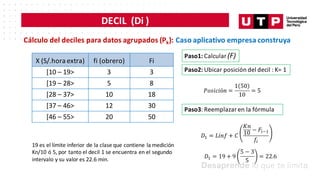
Tiempo de vida útil (Horas) N° de componentes(fi)
[500; 700> 6
[700; 900> 12
[900; 1100> 10
[1100; 1300> 8
[1300; 1500] 4
Total 40
Calcular e interpretar el coeficientedeasimetría correspondientea los tiempos en horas devida útil
de la muestrade40 componentes electrónicos.
Coeficiente de asimetría de Pearson (Ak)
Caso: Componenteelectrónico
Se realiza un estudio sobre el tiempo de vida útil de un componente electrónico. A continuación
se presenta la tabla de datos agrupados por intervalos para una muestra de 40 tiempos en horas
de vida útil de los componentes electrónicos en estudio:

37. MEDIDAS DE FORMA
1. Completando la tabla de frecuencias
Tiempo de vida
útil (Horas)
N° de
componentes(fi)
Marca de clase
(Xi)
Frecuencia
acumulada(Fi)
𝒇𝒊 .𝑿𝒊 𝑥𝑖
2𝑓𝑖
[500; 700> 6 600 6 3600 2160000
[700; 900> 12 800 18 9600 7680000
[900; 1100> 10 1000 28 10000 10000000
[1100; 1300> 8 1200 36 9600 11520000
[1300; 1500] 4 1400 40 5600 7840000
Total 40 38400 39200000
Coeficientede asimetríade Pearson(Ak)
Solución: Caso: Componenteelectrónico
+
Media
Varianza
Desviación estándar
S = 244.74
Mediana: Paso1: F
Paso2:
Paso3:
2. Calculando los estadísticos:
𝑃𝑜𝑠𝑖𝑐𝑖ó𝑛 =
𝑛
2
=
40
2
= 20
𝑀• = 900 + 200
20 − 18
10
= 940
𝑋
9 =
∑𝑋;𝑓;
𝑛
=
38400
40
= 960
𝑆…
=
∑ 𝑋;𝑓; − 𝑛𝑋
9…
𝑛 − 1
𝑆…
=
39200000 − 40 960 …
40 − 1
𝑆…
= 59897.44
𝑆 = 59897.44

38. MEDIDAS DE FORMA
Coeficientede asimetríade Pearson(Ak)
Caso: Componenteelectrónico
3. Reemplazando en la fórmula deAsimetría:
4. Interpretación: La distribución de los datos presenta una asimetría positiva.
𝑥 − 𝑀𝑒
𝐴𝑘 = 3
𝑠
𝐴𝑘 = 3
960 − 940
244.74
= 0.245

39. MEDIDAS DE FORMA
P10, P25, P75, P90: percentiles
𝑢
𝑃75 − 𝑃25
𝐾 =
2(𝑃90 − 𝑃10)
Curtosis
Estas medidas nos brindan información sobre el grado de deformación vertical
de una distribuciónde frecuencias en comparacióncon la curva normal que le
corresponde.Tipos de distribucionessegún su grado de curtosis:

40. MEDIDAS DE FORMA
a) Si Ku < 0.263, la distribución es Platicúrtica.
b) Si Ku = 0.263, la distribución es Mesocúrtica.
c) Si Ku > 0.263, la distribución es Leptocúrtica.
Coeficientede curtosis
Si el grado de apuntamiento es
menor que el de la distribución
normal.
Si el grado de apuntamiento es
igual que el de la distribución
normal.
Si el grado de apuntamiento es
mayor que el de la distribución
normal.

41. MEDIDAS DE FORMA
Caso: Casa prefabricada
La resistencia es una característica importante de los materiales utilizados en casas prefabricadas.
Cada uno de los 50 elementos de placa prefabricados se sometieron a prueba de esfuerzo severo
y se registró el ancho máximo (mm) de las grietas resultantes. Los datos registrados para la
muestra en estudio fuela siguiente:
Ancho máximo de la grieta (mm) N° de elementos de placa (fi)
[0.4; 0.5> 6
[0.5; 0.6> 14
[0.6; 0.7> 10
[0.7; 0.8> 9
[0.8; 0.9] 4
[0.9; 1] 7
Total 50
Calcular e interpretar el coeficientedecurtosis correspondientea los anchos máximos (mm) de las
grietas resultantes para la muestrade50 elementos deplaca prefabricados.
Coeficientede curtosis

42. MEDIDAS DE FORMA
2. Cálculo de las medidas de posición:
Ancho máximo de
la grieta (mm)
N° de
elementos de
placa (fi)
Frecuencia
acumulada
(Fi)
[0.4; 0.5> 6 6
[0.5; 0.6> 14 20
[0.6; 0.7> 10 30
[0.7; 0.8> 9 39
[0.8; 0.9] 4 43
[0.9; 1] 7 50
Total 50
Percentil Posición Fórmula Valor
P75 37.5 = 0.7+0.1x(37.5-30)/9 0.78
P25 12.5 = 0.5+0.1x(12.5-6)/14 0.55
P90 45 = 0.9+0.1x(45-43)/7 0.93
P10 5 = 0.4+0.1x(5-0)/6 0.48
Recuerde: para P75
Paso1: F
Paso2: Posición
𝐾
𝑛
100
=
75(50)
100
= 37.5 (4𝑡𝑜 𝐼𝑛𝑡𝑒𝑟𝑣)
Paso3:
𝑃75 = 0.7 + 0.1.
37.5 − 30
9
= 0.78
P90
P10
P25
P75
Coeficientede curtosis
Caso: Casa prefabricada
Solución:
1. Completandola tabla de frecuencias:

43. MEDIDAS DE FORMA
4. Interpretación: Losdatos presentan una distribuciónPLATICÚRTICA.
Percentil Valor
P75 0.78
P25 0.55
P90 0.93
P10 0.48
75 25
u
90 10
(P -P )
K =
2(P -P )
Ku =0.255556
Coeficientede curtosis
Caso: Casa prefabricada
3. Reemplazando en la fórmula decurtosis:

44. LISTO PARA MIS EJERCICIOS

45. MEDIDAS DE POSICIÓN Y
DE FORMA

46. EJERCICIOS PROPUESTOS
Se tiene los tiempos(minutos) en que 32 niños están frente a una computadora en
casa jugando algún juego On-line
[5,2 6,1> 3
[6,1 7> 5
[7 7,9> 9
[7,9 8,8> 7
[8,8 9,7> 5
[9.7 10.6> 3
TOTAL 32
Halle el Percentil 10 e interprete

47. EJERCICIOS PROPUESTOS
Se tienen las notas obtenidas en el curso de Administración de Empresas ,
de una muestra de n=80 estudiantes del ciclo 2020-2 de la UTP, información
recopilada por los Estudiantes de la FAYN de la UTP en el mes de abril del
presente año que se dan en el Presente cuadro:
Tabla dedistribución defrecuencias de80 estudiantes del curso deAdministración según sus notas
[Li - Ls ) Xi fi Fi
0 - 4 2 5 5
4 - 8 6 15 20
8 - 12 10 20 40
12 - 16 14 35 75
16 - 20 18 5 80
Total 80
Fuente: Encuesta realizada por los Estudiantes de FAYN de UTP. Abril 2019 .Lima-Perú
Calcular el Percentil 75 e interpretar

48. EJERCICIOS PROPUESTOS
El gerente General por víspera del aniversario de la empresa decide otorgar un Bono de reconocimiento siempre y
cuando se cumpla algunas condiciones. Se muestra los minutos adicionales que en los últimos 3 meses los
empleados se han quedado trabajando, una vez finalizada la jornada laboral, de manera voluntaria para cumplir las
metas.
X (minutos adicionales) fi (empleado)
[50 – 70> 30
[70 – 90> 50
[90 – 110> 65
[110 – 130> 30
[130 – 150> 25
Si el 55% de los empleados tiene un tiempo de permanencia adicional menor o igual a aproximadamente a 99.231
minutos, entonces el gerente general otorgara un bono de compras de mil soles a todos los empleados, sino pasa
ello. Todos se quedarán sin Bono este año. ¿Los empleados recibirándicho bono?

49. Y ahora nos toca interactuar en CANVAS. Usaremos el
foro de consulta para estar en comunicación
permanente, también tendrás que completar algunas
actividades programadas.

50. 1. ¿Cuál es la diferencia de dato agrupado y no agrupado?
2. Ventajasy desventajas de las medidas de posición.
¿QUÉ HEMOS APRENDIDO HOY?

51. FINALMENTE
IMPORTANTE
1.Medidas de posición
2.Medidas de forma:
Asimetria y curtosis.
Excelente tu
participación
Desaprende tus
limitaciones y estate
listo para aprender.
J
Ésta sesión
quedará
grabada para tus
consultas.
C
PARA TI
1.Realiza los
ejercicios
propuestos de
ésta sesión y
práctica con la
tarea
domiciliaria.
2.Consulta en
el FORO tus
dudas.

52. INDICACIONESA TENER EN CUENTE EN ESTASESIÓN
P
3
T
2
U
1
Video
La clase queda
grabada para que
puedas repasar
Materiales
Consulta la
diapositiva y lista
de ejercicios
Foro-Tarea
Resolución de
ejercicios y
comentarios