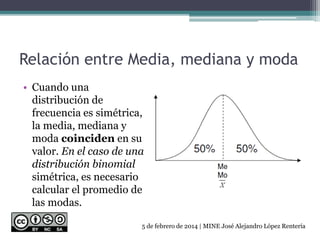
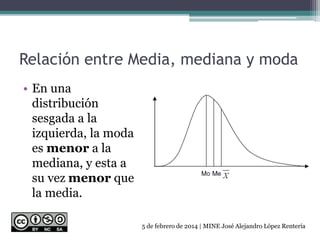
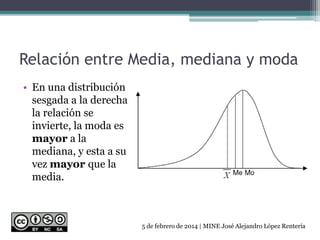
El documento describe las medidas de forma que permiten caracterizar las distribuciones de frecuencia. Explica que las medidas de forma incluyen la simetría, asimetría, concentración de datos y apuntamiento para clasificar la distribución. También define varios tipos de distribuciones como uniforme, simétrica, triangular, binomial y asimétrica. Por último, discute la relación entre la media, mediana y moda, así como cómo calcular el coeficiente de asimetría y curtosis.