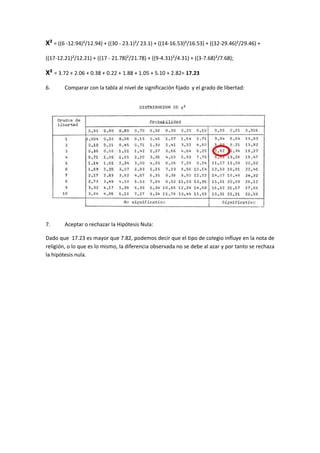
Este documento presenta los pasos para realizar una prueba de chi cuadrado para determinar si existe una relación entre la nota obtenida en religión y el tipo de colegio. Se proporciona una tabla de contingencia con los datos observados y se formulan las hipótesis nula y alternativa. Luego se calculan las frecuencias esperadas, el grado de libertad, el estadístico chi cuadrado y su comparación con un valor crítico. El resultado lleva al rechazo de la hipótesis nula, indicando que el tipo de coleg

1. Tenemos la siguiente tabla de contingencia que refleja los datos de la asignatura de religión
en centros escolares. ¿Influye el tipo de colegio en la nota obtenida . Margen de error 0,05:
1. Tabla con los datos observados:
2. Formular las hipótesis:
 Ho (Hipótesis Nula): La nota de los dos colegios es igual ó lo que es lo mismo no hay
diferencia en la nota en relación al tipo de colegio.
 H1 (Hipótesis Alternativa): La titularidad del colegio influye en la nota de religión.
3. Calcular las frecuencias esperadas o teóricas:
6 36×46/ 128= 12.94 17 34×46/128= 12.21
3036 ×82/128= 23.1 17 34×82/128= 21.78
1446×46/128= 16.53 9 12×46/128= 4.31
3246×82/128= 29.46 3 →12×82/128= 7.68
4. Calcular el grado de libertad:
Para calcular el grado de libertar, hay que restar el número de filas a 1 y el número de
columnas a 1, multiplicando esta resta:
(4-1)(2-1) = 3
5. Se calcular Chi Cuadrado. La fórmula es la siguiente:

2. X² = ((6 -12.94)²/12.94) + ((30 - 23.1)²/ 23.1) + ((14-16.53)²/16.53) + ((32-29.46)²/29.46) +
((17-12.21)²/12.21) + ((17 - 21.78)²/21.78) + ((9-4.31)²/4.31) + ((3-7.68)²/7.68);
X² = 3.72 + 2.06 + 0.38 + 0.22 + 1.88 + 1.05 + 5.10 + 2.82= 17.23
6. Comparar con la tabla al nivel de significación fijado y el grado de libertad:
7. Aceptar o rechazar la Hipótesis Nula:
Dado que 17.23 es mayor que 7.82, podemos decir que el tipo de colegio influye en la nota de
religión, o lo que es lo mismo, la diferencia observada no se debe al azar y por tanto se rechaza
la hipótesis nula.