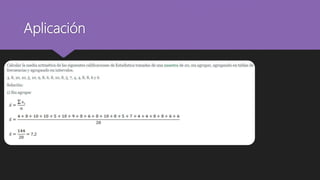
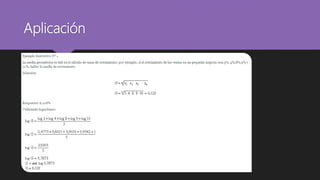
Este documento describe las medidas de tendencia central como la media, mediana y moda. Explica que estas medidas se usan para resumir conjuntos de datos y describir los valores típicos o promedios. También discute los diferentes tipos de promedios como la media aritmética, media ponderada, media geométrica y media armónica.

1. Hermary Florez C.I: 26.265.661
ESTADISTICA YV
Republica Bolivariana de Venezuela
Ministerio del poder popular para la educación
Instituto universitario Politécnico
“Santiago Mariño”
Sede- Barcelona

2. Medidas de tendencia central
 Las medidas de Tendencia Central son empleadas para resumir a los conjuntos de datos que
serán sometidos a un estudio estadístico, se les llama medidas de tendencia central porque
general mente la acumulación más alta de datos se encuentra en los valores intermedios. Estas
medidas son utilizadas con gran frecuencias como medidas descriptivas de poblaciones o
muestras.
Las mas empleadas
1. Moda - Es el valor con una mayor frecuencia en una distribución de datos.
2. Mediana – Representa el valor de la variable que deja por debajo de sí a la mitad de los datos
en un conjunto ordenados de menor a mayor.
3. Media – Promedio o valor obtenido por la suma de todos los datos (valores) dividida entre el
número de sumandos.

3. Importancia de las medidas de tendencia
central
Principalmente es de vital importancia saber que
estas medidas describen un conjunto de elementos
por la forma en que se comporta el centro de su
distribución.
Las medidas de tendencia central (media, mediana y
moda) sirven como puntos de referencia para
interpretar las calificaciones que se obtienen en una
prueba
Al describir las características típicas de conjuntos de
datos y, como hay varias formas de hacerlo, existen
y se utilizan varios tipos de promedios. Se les llama
medidas de tendencia central porque general mente
la acumulación más alta de datos se encuentra en
los valores intermedios.
Estas se destinan a resumir un conjunto de datos respecto a una
característica conservada o investigada, en solo número
considerado representativo Los resultados obtenidos con la
aplicación de estas medidas, pretenden explicar un conjunto de
datos mediante el valor representativo o típico.
El valor representativo es un valor que se calcula para describir
una característica que suele agrupar muchas clases de datos y
que se diferencian en la forma en que se definen típicamente, en
la cantidad y tipo de información. En resumen, los objetivos de
las medidas de tendencia central son: Mostrar en qué lugar se
ubica un dato promedio o típico del grupo de datos.
Sirve como un método para comparar o interpretar cualquier
posición en relación con las posiciones centrales o típicas.
Sirve como un método para comparar la posición obtenida por
un mismo parámetro en dos diferentes ocasiones, sirve como un
método para comparar los resultados medios obtenidos por dos
o más grupos

4. Tipos de promedios
 Los promedio más comunes conocidos en estadística son
 1).- La media aritmética,
 2).- la mediana,
 3).- la moda,
 4).- la media geométrica y
 5).- la media armónica.
Cada promedio tiene sus características particulares. La determinación de cuál de los
diferentes tipos de promedios deberá ser usado bajo diferentes circunstancias
depende grandemente de las características de los promedios. En general, los tres
primeros promedios son usados más frecuentemente los dos últimos son usados
solamente en casos muy especiales.

5. Tipos de promedios
 La media aritmética, o simplemente la media: es el tipo más comúnmente usado entre los cinco tipos
de promedios. Los métodos para calcular la media para datos no agrupados y para datos agrupados.
 media ponderada: A veces puede ser útil otorgar pesos o valores a los datos dependiendo de su
relevancia para determinado estudio. En esos casos se puede utilizar una media ponderada. es un
conjunto de datos o media muestral y son números reales positivos, llamados "pesos" o factores de
ponderación.
 La media geométrica es un promedio muy útil en conjuntos de números que son interpretados en
orden de su producto, no de su suma (tal y como ocurre con la media aritmética). Por ejemplo, las
velocidades de crecimiento.
 La media armónica :es un promedio muy útil en conjuntos de números que se definen en relación con
alguna unidad, por ejemplo la velocidad (distancia por unidad de tiempo).
 La moda: de un conjunto de datos es el dato que más veces se repite, es decir, aquel que tiene mayor
frecuencia absoluta.

6. Aplicación

7. Aplicación

8. Aplicación

9. Aplicación

10. Aplicación

11. Aplicación

12. Aplicación

13. Aplicación

14. Conclusión
 Los conceptos antes mencionados han sido analizados e
investigados de tal manera de hacer más fácil su comprensión y
entendimientos ya que la estadística es la ciencia que trata de
entender, organizar y tomar decisiones que estén de acuerdo
con los análisis efectuados.

15. Bibliografía
 CAMACHO, J. (2000) Estadística con SPSS versión 9 para Windows. Madrid: Ra-Ma.
 DIAZ de RADA, V. (1999) Técnicas de análisis de datos para investigadores sociales: aplicaciones
prácticas con SSPS para Windows. Madrid: Ra-Ma
 CANAVOS, G. (1988) Probabilidad y Estadística. Aplicaciones y Métodos. México: McGraw-Hill.
 Armando, Soto Negrin. Principios de Estadística. Editorial Panapo. 1999. Pág.: 71-81.
 Ernesto, Rivas González. Estadística General. Ediciones de la Biblioteca. Caracas. 2000. Pág.: 164-169.
 Conceptos Básicos de Estadística (S.F). Texto completo en:
http://www.gestiopolis.com/recursos/experto/catsexp/pagans/eco/44/estadistica.htm