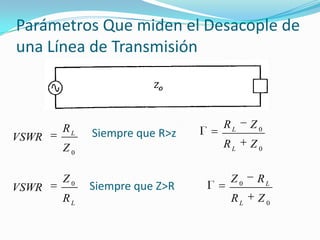
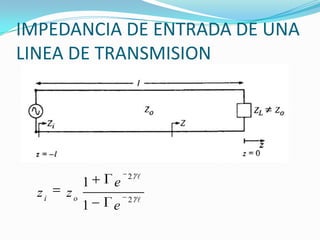
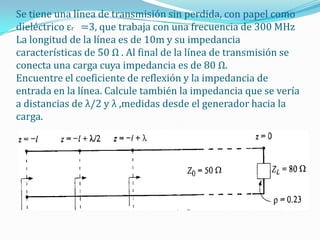
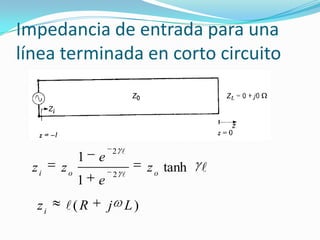
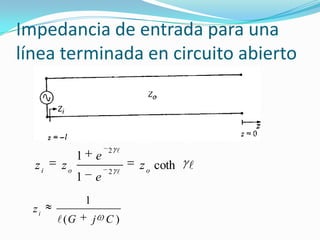
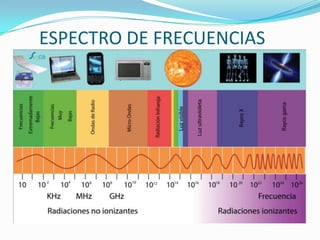
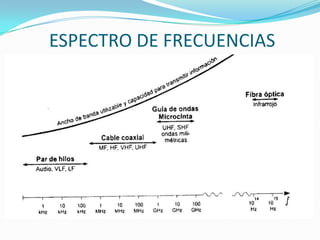
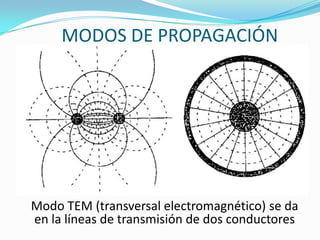
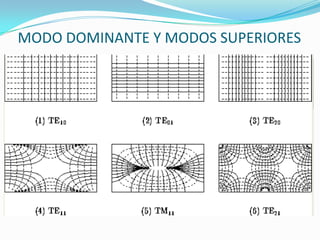
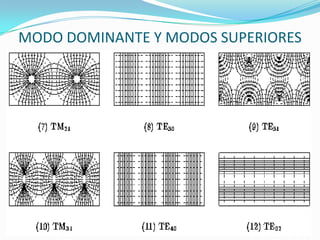
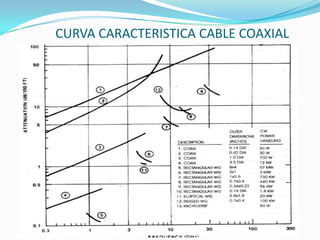
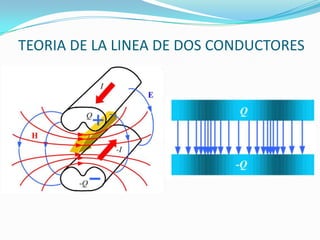
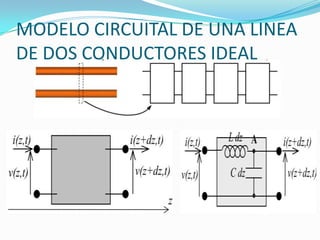
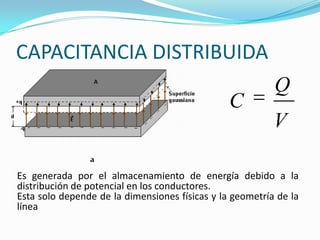
El documento trata sobre líneas de transmisión y sus características. Explica conceptos como modos de propagación, capacitancia e inductancia distribuida, impedancia característica, atenuación y velocidad de propagación en líneas de transmisión. También incluye ejemplos para calcular estas propiedades para cables coaxiales y bifilares.

2. GUIADOS
NO GUIADOS

3. MEDIOS NO GUIADOS

4. MEDIOS GUIADOS
BIFILAR COAXIAL UTP
GUIA DE ONDA FIBRA OPTICA

5. LINEAS BALANCIADAS /DESBALANCIADAS
DIAGRAMA DE UN BALUN
BALUN

6. ESPECTRO DE FRECUENCIAS

7. ESPECTRO DE FRECUENCIAS

8. MODOS DE PROPAGACIÓN
Modo TEM (transversal electromagnético) se da
en la líneas de transmisión de dos conductores

9. MODO DOMINANTE Y MODOS SUPERIORES

10. MODO DOMINANTE Y MODOS SUPERIORES

11. FRECUENCIA DE CORTE

12. PROPAGACIÓN MULTIMODO
CANAL
Cuando se propaga mas de un modo la energía se distribuye en
los diferentes modos los cuales tienen diferentes velocidades de
propagación y en consecuencia llegaran en distintos tiempos

13. INTERFERENCIA INTERSIMBOLO (ISI)
CANAL
ISI

14. CURVA CARACTERISTICA CABLE COAXIAL

15. TEORIA DE LA LINEA DE DOS CONDUCTORES

16. MODELO CIRCUITAL DE UNA LINEA
DE DOS CONDUCTORES IDEAL

17. CAPACITANCIA DISTRIBUIDA
Es generada por el almacenamiento de energía debido a la
distribución de potencial en los conductores.
Esta solo depende de la dimensiones físicas y la geometría de la
línea
V
Q
C
a

18. EJEMPLO: Deduzca la expresión matemática para
calcular la capacitancia distribuida de un cable
coaxial a altas frecuencias
a
b
aislante

19. EJEMPLO: Deduzca la expresión matemática para
calcular la capacitancia distribuida de un cable
coaxial a altas frecuencias
a
b
r
r
Q
D
2
Q
Densidad de flujo eléctrico
r
QD
E
2
Campo Eléctrico
b
a
r
Qdr
r
Qdr
V
22
)ln(
2
)]ln()[ln(
2
ab
Q
ab
Q
V
mF
ababQ
Q
V
Q
C /
)ln(
2
)ln(
2

20. EFECTO PIEL (SKIN)
Es el fenómeno en el cual, a una alta frecuencia la corriente
eléctrica tiende a circular en la mayor proporción sobre la
superficie (piel) del conductor y no en el interior de este.

21. INDUCTANCIA DISTRIBUIDA
I
L B
B Flujo Magnético
I Corriente
Es generada por el almacenamiento de energía debido a la
distribución de corrientes en los conductores.
Esta solo depende de la dimensiones físicas y la geometría de la
línea

22. EJEMPLO: Deduzca la expresión matemática para
calcular la inductancia distribuida de un cable
coaxial a altas frecuencias
a
b
aislante

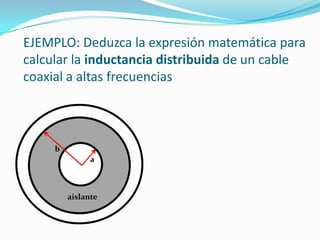
23. EJEMPLO: Deduzca la expresión matemática para
calcular la inductancia distribuida de un cable
coaxial a altas frecuencias
a
b
r
r
I
B
2
Q
Densidad de campo magnético
ABB
Flujo magnético
b
a
B
dr
r
I
dr
r
I
22
)ln(
2
)]ln()[ln(
2
ab
I
ab
I
B
mHab
I
ab
I
I
L B
/)ln(
2
)ln(
2

24. EJEMPLO: Determine la capacitancia e inductancia distribuida de
un cable coaxial RG-8 que posee un diámetro del conductor de
0,108’’ y un material dieléctrico semisólido de polietileno de
0,286’’ de diámetro
a
b
aislante
Material dieléctrico
Dieléctrico
Constante
(E)
Aire 1,00
Polietileno - espuma
celular (PE)
1,4
Polietileno - sólido (PE) 2,3
Poly tetrafluoroetileno
(PTFE)
2,1
Tetrafluoroetileno celular
poli
(PTFE))
1,4
Etileno propileno fluorado
(FEP)
2,1
Celular etileno fluorado
propileno (FEP)
1,5
Caucho de butilo 3,1
El caucho de silicona 2,08 a 3,50

25. Ecuaciones De Inductancia y
Capacitancia Para Un Cable Bifilar
)ln( adL )ln( ad
C

26. EJEMPLO: Una Línea Bifilar tiene conductores de Cobre
con radio igual a 2mm. La separación entre centros es
de 2cm y el material aislante es polietileno

27. MODELO CIRCUITAL DE UNA LINEA
DE DOS CONDUCTORES CON
PERDIDAS

28. RESISTENCIA DISTRIBUIDA
Es Ocasionada a razón que los conductores no son perfectos. Y dicho
valor depende de la conductividad del material, su geometría y de la
distribución de la densidad de corriente (que es función de la
frecuencia)
2

: La profundidad de penetración de la corriente
La densidad de distribución de
corriente es función de la
profundidad de penetración
mS /10
8

29. CONDUCTANCIA DISTRIBUIDA
Es Ocasionada a razón que los dieléctricos utilizados no son perfectos. Ya
que estos poseen cierta conductividad que crece con la frecuencia de
corrientes alternas y produce perdidas denominadas como histéresis del
dieléctrico

30. TABLA DE DIELECTRICOS

31. ECUACIONES PARA DETERMINAR
RESISTENCIA Y CONDUCTANCIA
DISTRIBUIDA
)
11
(
2
1
ba
R
C
 )ln(
2
ab
G d
CABLE COAXIAL
C
a
R

1
CABLE BIFILAR
)2(cosh
1
ad
G d

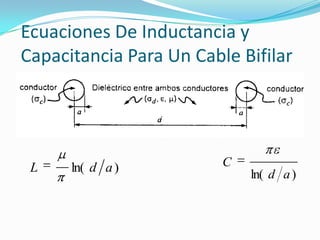
32. CONSTANTES DE UNA LINEA DE
TRANSMISION
))(( CjGLjR
CONSTANTE DE PROPAGACION
j
Constante de
atenuación
Constante de
Fase
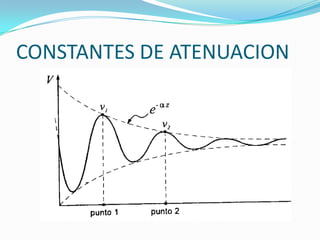
α indica la atenuación que sufre la onda de voltaje o de
corriente conforme se propaga a lo largo de la línea. Sus
unidades son [nepers/metro] 1nepers = 8,686 dB
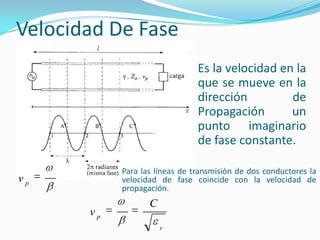
β indica la rapidez de cambio de la fase de la onda
conforme se propaga. Sus unidades son [radianes/metro]

33. CONSTANTES DE ATENUACION

34. IMPEDANCIA CARACTERISTICAS
)(
)(
CjG
LjR
ZO
Cada Línea de transmisión tendrá su propio valor
particular de impedancia características Zo ,
dependiendo de la geometría y las dimensiones de
la línea, así como la frecuencia de operación
Tenga en Cuenta

35. Encuentre la constante de Atenuación para
una línea de transmisión de 500 metros
w1500
W1250
m500

36. Velocidad De Propagación
Las ondas electromagnéticas no siempre se propagan a la
velocidad de la Luz (300000Km/s) si no que esta velocidad varia
dependiendo de la densidad del medio donde se propaguen,
disminuyendo en los medios mas densos
r
C
v
smC /103
8
relativaadpermitividr
__

37. Velocidad De Fase
Es la velocidad en la
que se mueve en la
dirección de
Propagación un
punto imaginario
de fase constante.
p
v
Para las líneas de transmisión de dos conductores la
velocidad de fase coincide con la velocidad de
propagación.
r
p
C
v

38. Parámetros Que miden el Desacople de
una Línea de Transmisión
0
Z
R
VSWR L Siempre que R>z
L
R
Z
VSWR 0
Siempre que Z>R
0
0
ZR
ZR
L
L
0
0
ZR
RZ
L
L

39. Perdidas de Retorno
Es una medida
que indica cuanta
potencia incidente
en la carga se esta
reflejando
2
Incidente
reflejada
P
P
LR

40. 100W de potencia de RF es aplicada a una línea de
transmisión sin perdidas con una impedancia
características de 50 Ω, terminada en una carga
resistiva de 25 Ω.
Calcule la potencia reflejada y la potencia en la carga

41. IMPEDANCIA DE ENTRADA DE UNA
LINEA DE TRANSMISION


2
2
1
1
e
e
zz oi

42. Se tiene una línea de transmisión sin perdida, con papel como
dieléctrico εr =3, que trabaja con una frecuencia de 300 MHz
La longitud de la línea es de 10m y su impedancia
características de 50 Ω . Al final de la línea de transmisión se
conecta una carga cuya impedancia es de 80 Ω.
Encuentre el coeficiente de reflexión y la impedancia de
entrada en la línea. Calcule también la impedancia que se vería
a distancias de λ/2 y λ ,medidas desde el generador hacia la
carga.

44. Impedancia de entrada para una
línea terminada en corto circuito


tanh
1
1
2
2
ooi
z
e
e
zz
)( LjRzi


45. Impedancia de entrada para una
línea terminada en circuito abierto


coth
1
1
2
2
ooi
z
e
e
zz
)(
1
CjG
zi
