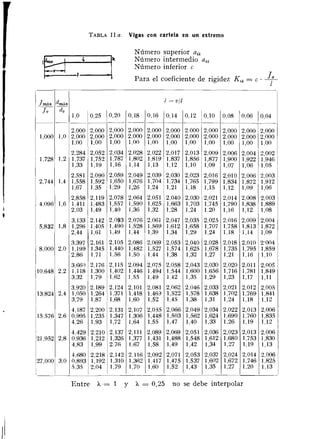
1) Este documento presenta un método simplificado y rápido para calcular estructuras de varios pisos teniendo en cuenta el desplazamiento de los nudos. 2) El método divide el cálculo en etapas sucesivas considerando primero nudos rígidos e ignorando el desplazamiento, y luego incorporando este factor. 3) El método ofrece ventajas como cálculos correctivos en cada nudo, facilidad para actualizar cargas o dimensiones de barras, y precisión comparable a métodos más complejos.

1. Dr. Ing. G . KANI
D E VARIOS P I S O S
METODO DE CALCULO SENCILLO Y RAPIDO
TENIENDO EN CUENTA EL DESPLAZAMIENTO
DE LOS NUDOS
E D I T O R I A L R E V E R T E , S . A.
Barcelona - Buenos Aires - MCxico
M C M L V l l l

2. T I T U L O D E L.4 O U R A OKIGIS.31.
DIE BERECHNUNG MEHRSTOCKIGER R A H M E N
(6: rtlicion)
Editada por
VERLAC,KOXRADWITTWER
Stuttgsrt
V E R S I ~ N E S P A ~ ~ O L AF O R
ENRIQUE R O D ~ N
Ingeniero industrial, Jefe dcl serviric~tecnico de
~Cubiertasy Tejados, S. A , , Compafila Grneral de Construcci.>ncs
@ E D I T O R I A L REVERT^, S . A.
DEP~SITOLEGAL B. 18307 - 1958
Reirnpresidn offset. - EDITORIAL LUIS VIVES. S. A. -ZARAGOZ.~

3. N O T A C I O N E S E M P L E A D A S
Mik Momento flector en el extren~o7 de la barra 2-k
-
Aftk Momento de empotramiento perfecto en el estretno I producido por
las cargas esteriores.
-
Ill, Momento de sujecion.
Momento en extremo i debido a1 giro del mismo
M'ki Momento en extrelno i debido a1 giro del extremo K
M"ik Momento dehido a1 desplazatniento del extremo z dc la barra 1-k.
--
MY
Q r h3Momento dcl piso =
3
Qr Fuerza cortante en piso r.
hr Xltura de la columna del piso r.
h Altura de una columna.
I
K = -
1
Coeficiente de rigidez (K = - - en barras de secci6n constante)
1 2
/Lik Coeficiente de reparto o factor de giro.
3
Factor de corrimiento o coeficiente de desplazamiento ( 1 1 = - -
2
en barras de secci6n constante).
hYc = - Factor de reduction en coluninas.
h
H Fuerza de fijaci6n a1 deslizaniiento
KANI.-1

4. Z Y B Lkngulosde giro de 10s extren~oscle una barra
T i k Akngu~ode giro total del estrerno 1 de la barra i-k
7‘'k ringulo de giro producido :,or la carga exterior en el extrelno z de la
barra I-k
m Factor de correccion.
o Desplazamiento de UII nudo
tingulo de desplazalniento transversal de uiia colulnnn
- - -
a i k h , k cih Coeficientes de barra
I'
11 '-L- Ordenada de :a linea de ii~fluencia.
0
0 hngulo de inflexion para la elistica.
'P P' Funciones para el cAlculo de la linea de influencia.
i Factor de acartelanliento.
/ D ~Iomentode inercia ell centro de la barra.
I Yalores tabulados para harra de inercia variable
'1,
-- Ya!or especifico de harra
hlk
Li Coeficiente cle elasticidad

5. In troduccion
Existen varios mCtodos para el calculo cle estructuras reticuladas.
En estos 6ltimos aiios el mhs difundido de todos ha sido el metodo de
CROSS, o de aproximaciones sucesivas.
En el caso de porticos de varios pisos, existe !a posibilidad del despla-
zanliento horizontal de 10s nudos. En su calculo, se supone a veces que
10s nudos rio pueden desplazarse, o sea que son fijos, lo cual abrevia dicho
cAlculo extraordinariamente, pero no permite estudiar la action de las
fuerzas horizontales (viento), pues &stasson, en esencia, fuerzas horizonta-
les clue producen un desplazamiento de 10s nudos.. 1,os chlculos estiticos requieren a veces gran precision (hasta el 1 O , ) ,
y el hecho de despreciar el desplazamiento horizontal de 10s riudos puecle
dar errores tar1 gralldes que lleguen i~iclusoa cambiar el sign0 de 10s
moinentos; por este nlotivo, y esto es lo que se trata ell este libro, se ha
buscado un nuevo rnCtodo de cilculo de 10s desplazamientos horizolltales
que simplifique su obtencion.
Debo advertir, desde un principio, que es erroneo supoiler clue u11
nit:todo de ccaproximaciones sucesivas))sea por ello un m6todo aprosirtlado,
pues un mCtodo aproximado, es aqui.1 que proporciona en realidad resul-
tados aproximados, y 10s mktodos de ccaproximaciones sucesivaso dan
resultados con la precision que se desee, cuando se continua el cilculo
hasta llegar a apurar estos resultados
En uii mktodo calificado conlo ccexactou, resuelto, por ejemplo, rne-
cliante el planteamiento' de las ecuaciones de deformacibn, 10s resultados
ol~tenidosson tambiCn hasta cierto punto aproximados, pues dependen
tlt.1 iiumero de cdras decimales con que ccllculen~os10s resultados de las
rncoqnitas. Cn metodo de naproximaciones sucesivaso (como por ejen~plo
t-1 rn&todode CROSS) puede llegar a la nlisnla exactitud en 10s resultrdos
i!ue un miltodo c,esacto)), continuando las iteraciones liasta donde que-
r.ilrlos. Es, por 10 tanto, absurdo, designar a dos procedimientos de cilculo

6. 4 P d R T l C O S DE 1'.4 RIOS PISO.5
que llegan a 10s mismos resultados, uno como ccexacto))y el otro como
ccapro~imado))~.
El mittodo de calculo expuesto en este estudio es, por lo tanto, un
mktodo de ccaproximaciones sucesivas)) y tiene, comparado con otros mk-
todos, las siguientes ventajas:
1. En el supuesto de nudos fijos, o sea sin considerar el posible des-
plazamiento de 10s mismos, el calculo es, en este mktodo, cccorrectivo))en
cada nudo, pasando luego de kste a otro cualquiera, con lo cual, ademhs
de un ahorro de tiempo, supone lnuy poca probabilidad de que se cometan
errores en el mismo.
2. La introducci6n en el c~lculode la hip6tesis de iiudos desplaza-
bles supone una pequeca variaci6n en el desarrollo del mismo, que no tiene
gran importancia.
3. Este mktodo, por ser cccorrectivo)),puede llanlarse con ccelirninacion
automatics de 10s erroreso, debido a que dicho error desaparece a1 produ-
cirse sucesivas iteraciones.
4. La comprobaci6n de 10s resultados (que se obtiene por suma de
unos pocos valores) puede hacerse en cualquier nudo y en cualquier mo-
mento, sin que sea necesario para 10s t6cnicos inspectores el conocer el
detalle del calculo que ha llevado a1 resultado definitivo.
5. Para el caso de que deban variarse 10s tipos de cargas o seccion
de las barras posteriormente a1 cAlculo efectuado, no es necesario l~olver
a empezar el mismo, sino s6l0 anotar 10s cambios y repetirlos unicamente
en parte.
ti. I,a variaci6n de inercia de las barras puede teilerse fAciln~ente
en cuenta (conlo se vera en el cap. VI). El tener en cuenta la existencia de
cartelas, frecuentes en obras de hormig6n armado, representa un aumento
de trabajo muy pequeiio en el calculo, sin que esto signifique clue la exis-
tencia de ellas tenga pequeiia importancia en 10s resultados.
Todo lo dicho para las estructuras de varios pisos puede tambiPn
aplicarse a1 caso de tratarse de vigas continuas con apoyos elasticamente
empotrados.
T:s, por lo tanto, rtna cuestibn dc definicibn, la cxactititd de detcrminadu metorlo de
c6lculo. En matemiticas, por ejemplo, no pue(1e dcrirsc quc- un metoclo es aprosiniado, cu;uitlo a?
Ilcza a resultados de una esactitud r~revia~nentefiiadn.
,~-
Otra c ~ s aCS, POI cjctnplo, hnllar In raiz cuadratla tlc un ni~nicroI/104!)00 = 33(! en lugar-
ilc calcolar la de Z/10~901,q ~ r cc i e! ni~mvrurcnl, pues, en cste caso, In csactitud depende dcl
numero consi(lerado, sin que 11ucda ilccirsc clue cl pr~~cr(limi?ntors aprnximado. 'nicnmcnte
a1 terrni~iar1111 crilcrllo sr p ~ ~ d r i ihahTar de ii el ~ n r t o d oha siclr) exact0 < I aproximado.

7. I. Definiciones
El objeto del cAlculo estitico de una estructura es obtener el equili-
brio de la misma, cuando, a1 cargar sus distintos elementos, giran y se des-
plazan 10s nudos de aquklla.
Conocidos 10s momentos flectores en 10s extremos de cada una de las
barras, queda determinado el cAlcu1o de la misma, pues 10s demks valores
estaticos pueden deducirse de estos momentos, por lo cual el cAlculo consis-
tira esencialmente en la deternlinacion de 10s momentos en 10s extremos de
cada barra. En cada nudo actiian dos momentos, iguales y contrarios, uno
de ellos, que gira con el extrenlo de la barra, es el que debernos considerar
como momento en dicho extremo,
y el otro el que actiia exteriormente
sobre el citado nudo.
Adoptaremos para signos de 10s
momentos flectores la regla indicada
ry-~ M.
a continuaci6n, aunque sea distinta
de la corrieritemente usada en otros FIG. 1
tratados:
Se considera corno jbositiz~oel momento flector en el extrerno de zlna barra,
cllando SLL sentido de giro es el de las agzljas del reloj (fig. 1).
Esta nlisnla regla se aplica para cualquier otro momento (por ejemplo,
monienfos de fijaci611, momentos de nudo), asi conlo tambi6n para 10s
angulos de giro.
Cuando actiia sobre un ~iudoun niomento flector exterior de sentido
positive, el nudo y todos 10s extrenios de las barras que concurren en 61
recibe~i~liolnentospositivos en este extremo.
I,os ~iudosde la estructura se designaran con un numero de orden
(1, 2 , 3, etc.), o en la exposicion de la teoria con letras i , k , 1, m, etc.
El rnoniento flector en el extrenlo i o k de la barra i - k se desig-
nara, conlo puede verse en la figura 1, con M,, o Mki, respectivamente.
En este caso el primer subindice indica el extrenlo en el que actiia el
xllomelito.

8. 1,as t~lulnentose n los rstre~nostie Irr bnrra i-k producidos por las cargas
exteriores, suponiendo enipotramieilto perfecto en ambos extremos, 10s
designareillos coil JI,, o ,u,,respectivamente.
I'ara 10s distintos tipos de cargas corrientemente usadas, se pueden
encontrar sus -alores en 10s n~anuales~.
1,as caracteristicas de uila barra de una estructura se definen por
el rrioi~ientode iiiercia de su secci6ti y por su longitud. La relaci6n
entre estos dos l~aloresse designa, a1 objeto de abreviar, con el valor
I
K = - (coeficiente de rigidez) enipleado tambii.11 etl el 111ttodode CROSS.
1
Empezaremos el cilculo suponiendo que a1 actuar las cargas exte-
riores existe empotmnziento perjecti~ en 10s dos estrenios de cada barra, o
sea, que 10s nudos permaneceii fijos sit1 poder efectuar tlingun giro ni
desplazatniento. Cada barra es, por lo tanto, como una viga de utl trnmo
en~potradaen sus extrenios, para 10s cuales nos sera facil calcular 10s
correspondientes iiionientos de empotran~iento.
A las fuerzas y nionlentos exteriores que iinpiden el desplazamiento
y el giro de estos nudos las llaniaremos jzterzns y momentos de szrjeciuln.
Deternlinados 10s nlomentos de empotran~ientoen 10s tludos, se calculan
luego 10s nioiiieiitos y fuerzas de sujeci6n en cada uno de ellos. El hecho
de esistir equilibrio en un nudo i , equivale a expresar que el momento de
-sujeci6ti .IFi debe ser igual a la suma de todos 10s mon~entosde empo-
tramiento de las barras que concurren en diclio nudo, asi:
(Existe igualdad de signos, ademis de la de 10s valores, debido a que el
niomento de sujeci6n actiia sobre el nudo 10s de enlpotramiento en 10s
estrenios de las barras.)
Beton Icalender - (Cale~tdariode hormighn);
Stahll~auKalender - (Cale~~dariodrl acero);
TokaOcyn: Rnhmentafeln - iTal>laspara phrticos)

9. II. Estructuras con nudos rigidos I
ESTIJI)IODE LOS ANGULOS I)l3 GIRO
1211esta primern etapa de cAlculo se supone clue 10s tiudos son indes-
plnzables.
Cuando se defort~lautla estructura bajo la acci6a de ciertas cargas
exteriores, sit1 suponer que existe rigidez en 10s tiudos de la niisma, cada
uno cle ellos gira en un determinado valor; por
ejet~~plo,para ulia barra i-k el extrel~ioi girara
eti uli angulo t,y el extremo k en un atigulo t,.
Vamos a descoin~mnerel giro total de 10s extre-
mos de la Imrra i-k, cot110 superposici6n de las
tres siguientes y sucesivas etapas (vkase fig. 2):
1. I,n barra i-k se defornia, flexando, bajo
la acci6n de la carga, sin girar 10s extremos
de la misma.
2. El extrqmo i gira en uii Angulo t i ,
lnielitras el extremo k no gira.
5. El extremo k gira en t i , mientras el
extrerno i no gira.
E l valor total del momento en cada
extremo sera igual a la suma de las tres etapas FIG.2
consideradas.
I'or ejemplo, para el extremo i de la barra i-k se compondrh de:
Valor M,, debido a la carga exterior (momento de empotranliento
perfecto en el extremo de la barra).
Valor 2 M',, debido a1 giro del propio extremo i.
Valor Mrkidebido a1 giro del otro extremo k de la barra.

10. Se puede, por lo tanto, escribir para el extremo i de la barra i-k:
-
.Ifik = .lik2 ,ll'ik+ (1)
El valor Mrikdebido a1 giro t, del extremo i es proporciona13 a1 An-
gulo t, y a la rigidez k de la barra y se designarA corno influencia del giro
del estremo i. AnAlogameiite, el momento Mfkies proporciorlal a1 Angulo
de giro z, )- a la rigidez k de
la barra, y se designara
corno injlue~zciadel giro del
ofro exfremo k .
Conocidos estos valores,
podrenlos obteiler el mo-
tnento total Mi,,niediante
la ecuacion ( I j, por suma de
10s mismos, o sea:
del momento de empotra-
nlieilto perfecto en el
extremo,
del inomellto dehido a1 giro
tlel propio e s t r e m o y
1-aoo 1 6w 1 s,oo t (lel momento debiclo a1 giro
tlel extrenio coiltrario de
In harrn.
-an~osa calcular sepn-
radmilente cada uno de estos
1. valores, ell lugar tle calcular directamellte el nlomento total, tle lo cual
:I se deril-a precisnmente, conio henlos dicl~oen la introd~iccion,la ventaja
tle este 1116totlo.
1, I,as s~~cesi.:is1-ariaciones del nlonlento flector se obtendra~len cada
nutlo, ])or la reiteracihil tle una iuisnia operncihi1. I'or una sucesion arbi-
traria tle uno a otro nudo de la estructura, y reiterando en cad3 uno de
!'
ellos la 111isn1aoperacihn, puecle llegarse a conseguir el grado de nprosi-
niacitill clue se tlesea:
,I Yamos a es1)oner el tlesarrollo del cAlculo, ~nediantela resoluci611 de
un ejenllilo (-kase fig. 3).
1 1,as rigitleces k tle las distintas harras se aiiotan ell el centro de cada
una tle ellas ell la figura 3, doncle, ademAs, se indican 10s valores de las
cargas esteriores y las longitudes tle las barras cle la niisma.
d(nr(le 1: cs el 1nhcln111rli. rln.;ticidarl dcl material d r la tnrm.

11. 'so~!q!sodomosoqsaiaplapso[,iso.llc5su
ourosopls!ubz!ouraqxralauaolua!uxa~aoduxaapso$uamt~msolaidmarssomal!q!xssa[ensoliod
'oqsalsplaeledouoiad'~e~uvz!ioqelieqannapopla!nhz!ouxaqxa[Buapuodsaiio~anbsoleied
sp!~c~sasoluamomso1vlsdepe~dopesotrZ!sapu!,!svlouu1anhslrransualauaaaqdpas
.,s~urs!u~sclapssfaso1apem!srralodd
sa~ua!puodsarlosselleqs-elapsouralJxasolua'nge1n8!3-e~rra.soru-e~oue
soldsaJua!llossalenrrerusolapselnurlqjselaqueypamsomelnsIessol
salo!laJxase81e3selwedopapado?ua!urel~odruaapsoTrrauroursotl
.elleqepe3apsouralJxasoluasalopsoA!sasnsso1nq!l3sa
alrurladsouanb'vern%!~elapeuranbsaapod!~lasorueqdopv

12. 10 P 6 R T I C O S LIE 17AR I O S PISOS
1,os valores de 10s momentos de empotramiento en la barra 1-2, por
ejeniplo, que tieile una longitud I = 4,00 m y una carga q = 1,8mt (y que
seran iguales para las barras 1-5 y 8-9, que se encuentran en idirnticas
condiciones) valen:
en el extremo izquierdo:
4I'
M , ,= - --- -- ~-2,40 111t
12
y en el extremo derecho:
4 I'
ilf,,, = + ---- = + 2.40 t l l t
12
Para las demis barras de luces distintas a irstas, pero iguales entre
si, y con la nlisma carga anterior q = 1,8mt, obtendremos unos valores
del momento de empotranliento de -8,60 mt en extremos izquierdos y
de +11,80n ~ ten 10s derechos, cuyos valores anotamos en figura 3 a.
Seguidamente se escriben 10s momentos de sujeci6n en el circulo
dibujado en el centro de cada nudo. Los momentos de sujeci6n que son 10s
que mailtienen la rigidez del nudo a1 giro del niismo soil iguales, con10
henios dicho anteriormente, a la suma de todos 10s momentos de empo-
tramiento en 10s extremos de las barras que coilcurren en el nudo.
Tendremos, por lo tanto, para el nudo 2:
,A continuaci6n, iremos determinando las variaciones que producen 10s
giros sucesivos de 10s nudos.
Podemos sentar, en principio, que: a1 girar uno cualquiera de 10s nudos,
las barras que concurren en el mismo giran del mismo angulo y que la
influencia de estos giros angulares, sobre 10s momentos en 10s extremos
de las barras que concurren en el nudo, dependen 6nicamente del valor del
angulo de giro y de la rigidez k de la barra correspondiente3. Cuando gira
unicamente un nudo de la estructura, ejerce este giro solamente influencia
sobre 10s momentos de las barras que concurren en el mismo, repartikn-
dose proporcionalmente a 10s valores de las rigideces respectivas, o sea,
expresindolo de otra forma, cuando conocemos la totalidad de 10s valo-
res que producen este giro, podemos determinar la parte que corresponde
a cada una de las barras, repartiendo esta suma proporcionalmente a las
rigideces de cada una de ellas.
Designaremos como extremo contiguo, el extremo de una barra que
concurre en un nudo y como extremo opuesto el otro extremo de la nlisma,
o sea, que a cada nudo corresponderi la misma cantidad de extrenios
contiguos como de extremos opuestos. (Una viga en voladizo puede con-
siderarse como una barra cuyo extremo opuesto se ha alejado en un va-
or infinite.)

13. Considerando el equilibria en un nudo cualquiera i , resulta5 que el
~nnmefztototal de sujecidn Gi nzds la szlnza de 10s vzomentos debidos a1 giro
del extrenzo opuesto de la barm, es decir
es igual a la suma de 10s monientos debidos a1 giro del propio extremo
multiplicado por (- 2).
Cuando conocenlos el valor del ingulo de giro en el extremo opuesto
del nudo considerado, podelnos seguidamente determinar su influencia
en el momento flector en el extremo adjuiito a1 nudo referido. Cuando 10s
valores de estos ingulos de giro 10s conocenlos s610 aprosiniadainente,
podenlos obtener tarnbii.11 10s valores del moineiito flector citado apro-
ximadamente, pero cada vez con mayor exactitud si reiteramos el cilculo
de 10s misnios. 1,os primitives x~alores,cuando no teneiiios. ninguno co11o-
cido, 10s podemos suponer iguales a cero.
En las sucesivas iteraciones para obtener mayor aproximacion, se
procede del siguiente modo:
Se suma a1 rnomento de sujecion del nudo 10s valores aproxiniados
de 10s momentos en 10s extremos opuestos de las barras, esta sunia se
divide por (-2) y el resultado se reparte entre todas las barras en la rela-
cion de rigideces k de las misrnas.
Es posible simplificar esta operacibn, introduciendo 10s factores de
giro (o coeficientes de repartici6n) que se obtienen repartiendo propor-
cionalmente a las rigideces de todas las barras que concurren en el nudo,
el valor total - . [Es decir, que la suma de 10s factores de giro de
un nudo debe ser qua1 a , por ser adeniis negativos.]
En el esquema de la figura 3 a se han anotado por cada nudo 10s va-
lores de estos factores de giro. La marcha a seguir para el cilculo de las
influencias de 10s giros seri, por lo tanto, ahora, como sigue:
S e suma el momento de sujecidn del nudo con 10s monzentos flectores
en 10s extremos opuestos de las barras que concurren en e'l. St?multiplica esta.
suma $or 10s factores de giro de cada barra, y 10s resultados son las inflzien-
cias de 10s giros sobre el momento flector en el extremo de cada barra.
Cuatido en la ecuacibn de cquilibrio S 41;;= 0 que debe cumplirse en cada tltldo i, sus-
(0
tituimos cste morneuto M;k por su valor dado por la ecuacibn (1)ohtetiemos
en la cual cl primer miembro es el momento de sujeciS11del nudo i, resultando:

14. 12 P 6 R T I r ' O S DE V A R I O S P I S O S
Keiterando esta operacirin en 10s sucesivos nudos en una marcha
arbitraria, se pueden hallar 10s valores sucesivos debidos a 10s giros en 10s
extremos opuestos de las barras que concurren en 61, con la aproximacirin
deseada.
Continuemos ahora con el ejemplo de la figura 3 a. Vamos a calcular
10s factores de giro para el nudo 9. 1,a suma de 10s valores de las rigideces K
de las barras que concurren en 61 es (v6ase la fig. 3):
El reparto de en la relacirin a las rigideces K da:
las cuales se allotan en el nudo 9 de la figura 3 a.
Conlo comprobacirin se sunlan 10s valores de estos factores de giro
en el nudo, que debe ser igual a
1
En la figura 3 a hemos allotado 10s nlonlentos de einpotramiento per-
fecto, 10s monlentos de sujecidr~y todos 10s factores de giro, y henlos calcu-
lado las influencias de 10s giros en tres iteraciones, con aproximaci6n su-
cesiva. Se ha enlpezado por el nudo 3, en el cual se han supuesto iguales
a cero las influencias de 10s giros en 10s estremos opuestos. Los valores
aprosinlados ohtenidos de este nudo se hail anotado en 10s respectivos
estremos de las barras del esquema (en las vigas por dehajo de sus ejes).
Coillo puede ohservarse. 10s primeros valores han dado ya una huena apro-
simaci6n.
El orden seguido para 10s nudos no influye en el resultado total, pero
si en la rapidez de la conr-ergencia de 10s resultados. KO dehenlos seguir,
por lo tanto, la marcha nlAs c6moda que seria en el orden de la numeraci6n
de 10s nudos, sin0 empezar sienlpre por el nudo mhs descon~pensado,en este
caso el nudo 3.
Siguiendo coil la demostraci6n del nlktodo de c&lculoempleado, con-
tinuamos en la figura 3 a con la cuarta iteraci6n. Para el nudo 3 sumamos
el momento de sujecirin y las filtimas influencias aprosimadas de 10s giros
en Ins estren~osopt~estosde las barras:

15. Teniendo en cuenta que 10s factores de giro (o coeficientes de repar-
tici6n) tienen signo negative, 10s valores de 10s giros de 10s nudos, y la sunia
que hemos obtenido, tienell siempre signo contrario; es decir:
estos valores se anotail en 10s respectivos extremos de las harras del
esquema, o sea, debajo de 10s valores -6,77 y -0,56 respectivamente.
Para el nudo 2, se obtiene como sunla de las influencias:
~iiultiplicandopor 10s factores de giro, obtenemos:
.If',,, = - 13,1R . (- 0,"s) = + S,62
M',,, = - 13.49. i- 0,214) = + 2,89
dl",,j = - 13.49 . (- 0,018) - + 0,24
en la dltinia iteraci6n en el iludo 7 se observa que, calculando s610 con
dos cifras decitnales, no se ha obtenido camhio apreciable con la anterior.
En las iteraciones de 10s nudos 1 y 4 se han ohtenido variaciones muy
pequefias en 10s hltin~osvalores, y en 10s otros nudos hat1 sido nulas. Cuan-
do es suficiente la aproxitnaci6n de dos decimales, no es necesario conti-
nuar Ins iteraciones.
En 10s extremos de barras enipotradas, en nuestro caso 10s pies de
las coluniilas del piso inferior, las influencias de 10s giros en estos nudos
soil nulas, yn que el Angulo de giro para cualquier deformaci6ri es cero.
Uila ventaja de este mktodo es, con10 henios dicho, que 10s errores de
cBlculo se eliminan con las sucesivas iteraciones. La probabilidad, adeniBs,
de coineter un error, es n ~ u ypequeiia, ya que sienipre consiste en la repe-
tici6n de una operation aritniktica muy sencilla, y 10s errores en la con-
sideraciciii de 10s signos son casi imposibles. (Obskrvense las operaciones
desarrolladas en varios nudos.) Si a pesar de todo se comete algun error,
bste 110 influye en el resultado final, sienlpre que no lo haya habido en
10s valores calculados para 10s niomentos de sujeci6n y 10s coeficientes
de repartici6n.
El sucesivo cBlculo de las influencias de 10s giros va siguiendo sien~pre
ulia niarclia con aproximaciones sucesivas de 10s mismos. A1 cometer uii
error, por lo tanto, 10s valores ohtenidos no es que Sean falsos sino nienos
aprosi~lladosque 10s siguientes. Daremos por terminado el cAlculo cuando,
ell la ultinla iteration, 10s valores obteniclos son casi iguales, y conio es muy
difieil que repitarnos el tnismo error en las ultimas iteraciones pode~nos
considerar, sin lugar a duda, que el ultimo valor es bueno.

16. 14 PORTICOS U E VARIO.5 PlSOS
Determitiadas las influencias definitivas de 10s giros, podemos obtener
10s momentos definitivos sumando 10s valores segun la ecuaci6n
Para mayor claridad, se ha hecho el cBlculo de 10s rnomentos clefi-
nitivos en la figura 3 b en lugar de liacerlo en la 3 a.
"s aconsejahle emplear para las sumas una maquina sumadora (que puede scr del tipo
de bolsillo) en la cual se suman 10s valores positives y ncgativos y que, junto con la regla de
cilculo, constituye~lunos buenos nuriliares del niisrno.

17. En la rnisma, se anotan 10s nlomentos de empotra~nientoperfecto,
v las influencias de giro obtetlidas en la hltima iteracicin, en 10s extremos
he las barras correspondientes. De acuerdo con la ecuacicin (I), obten-
dremos 10s momentos definitivos su~nandoa 10s valores anotados en $1
extremo de una barra 10s valores de la influencia del giro en el propio ex-
tremo y la del opuesto. Es decir, sumanlos en cada extrerno a 10s valores
apuntados un nlis~novalor, que es la suma de las influencias de giro en 10s
dos extremos. Por ello, en el extrenlo de cada barra se anotan ndenias
del valor del momento de empotramiento J- de la influencia del giro, la
sulna que acabamos de indicar.
I,a sulna de estos tres valores (en las columnas seran dos, por no exis-
tir niotllentos de empotramiento) es el momento total, que se anota en
cada Sarra por debajo de la tinea de suma.
Para la comprobaci611del cilculo (caso de Ingenieros inspectores) no es
necesario aconlpaiiar todo el desarrollo efectuado, pues basta con 10s valo-
res de la figura 3 b, donde se lian obtenido 10s resultados finales. En ella
se puede comprobar la marcha seguicla, e incluso registrar 10s valores de las
influencias de 10s giros en un nudo, efectuando en uno cualquiera de ellos
las sucesivas iteracioiles para la obtetlci6n de la influencia de 10s giros.

18. Debido a la condici6n de equilibrio en un nudo cualquiera, la suma de
10s momentos definitivos debe ser igual a cero (except0 en nudos en que
actuen momeiltos exteriores).
Si se hubiera cometido un error en el chlculo de estos momentos, que-
daria, por lo tanto, a1 descubierto a1 no set igual a cero, o igual a1 mo-
nlento exterior que actua en el nudo, la suma de 10s momentos definitivos
en un nudo.
Si precisanlos cambiar, a1 final del chlculo, la secci6n de las barras
de la estructura o de las cargas que act6an sobre la misnia, no es nece-
sario repetir el nlismo. Basta cambiar 10s valores en el chlculo anterior,
tomar como valores aproximados las influencias de giro obtenidas 4- con-
tinuar el calculo sobre las mismas. Bastan entonces una o dos iteraciones
solameilte en 10s nudos contiguos a 10s valores que ha11 variado, hasta
llegar a la nueva aprosimaci6n deseada.
Antes de dibujar el diagrama con 10s momentos definitivos en
10s extrenlos de las barras, debemos asegurarnos de que 10s sig~iosde 10s
mismos Sean 10s verdaderos, de acuerdo con la regla de signos adoptada.
Un momento es positivo cuando hace girar el extremo de la barra sobre
la cual actha, en el sentido de las agujas del reloj.
Un momento flector positivo en el extremo izquierdo de una barra
da lugar a tracciones en las fibras inferiores de la misnla; un moniento
positivo en el extremo derecho de una barra da lugar a tracci6n en las
fibras superiores.
Dibujado el grAfico de momentos flectores, conlo es costunlhre, de
manera que estos monlentos queden por la parte de la barra en la que se
producer1 tracciones, 10s momentos positivos debera11 dibujarse para 10s
estremos izquierdos hacia abajo del eje de la barra, 5- hacia arriba para
10s extremos derechos de las mismas.
El diagrama del ejeniplo estudiado se representa en la figura 3 c.
Cuando alguna de las barras de la estructura esti articulada en un
extrenlo (por ejemplo, colunlnas articuladas en su apoyo o vigas apoyadas
en uno de sus extremos), deberh introducirse una variaci6n en el chlculo,
teniendo en cuenta lo que explicamos a continuaci6n.
Conlparemos una colun~nacon un coeficiente de rigidez K que est6
articulada en el pie, con otra perfectan~enteempotrada en el mismo y cuyo
Q
3
coeficiente de rigidez es K' = - K. Se puede encontrar que para el
4
nlismo valor del angulo de giro en la cabeza de las columnas, el niomeilto
definitive es el niismo para ambas. Consideraren~os,por lo tanto, las
barras de la estructura con articulaci6n en u11 extremo, como )arras per-
9
3
fectanle~lteenipotradas cuyo coeficiente de rigidez es igual a - del de
4

19. la barra con articulaci6n. I,os valores de 10s momentos de empotranliento
a considerar para 10s extremos de estas barras, son 10s mismos que para
una barra de igual longitud, coiltitiuando luego el cAlculo como si estas
barras estuvieran perfectamente empotradas, teniendo solamente en cuenta
para el -alor del niomento definitive, que en el apoyo articulado su valor
es igusl a cero.
Para el caso de una estructura simktrica, y carga tambiitu si~nktricn,
es suficiente el cAlculo para la initad de esta estructura. Cuando el eje de
simetria pasa a lo largo de una columna (o sea el caso de un nutnero par
de tramos) 10s nudos de este eje no experimentan ning6n giro. rueden
considerarse, por lo tanto, como nudos con empotranliento perfecto. Cuando
el eje de sinletria pasa por el centro de 10s tranios de las barras horizouta-
es (o sea, para un numero impar de tramos), se puede sustituir cada una
de estas barras, despu6s de calculados 10s momentos de enipotraniiento,
por una barra mitad de lo~igitudempotrada en dicho eje de simetria y
con un valor del coeficiente de rigidez K' igual a la mitad de su coeficien-
te K correspondiente a la barra primitiva. (Cuando se deforma una barra
sim6tricamente respecto a1 centro de la misma, de tal manera que sus
extremos girail en un Angulo igual pero siniittrico, hay una misnia rela-
ci6n erltre 10s nionientos y 10s Angulos de giro en 10s extreinos, que entre
10s momentos y Angulos de la barra equivalente por la cual se ha sus-
tituido.)
1,os extreinos de las barras en voladizo (o cantilever) se pueden con-
siderar conio una barra cuyo estrenio opuesto estA a m a longitud infinita.
El valor del coeficiente de rigidez K de esta barra es igual a cero y el rno-
mento de empotramiento el de una barra cualpiera.
En el caso de actuar un moniento exterior sobre uno de 10s nudos,
pueden considerarse conio si fueran debidos a una m6nsula que se apoyara
en este nudo, y, por lo tanto, esta ni6nsula no influye para nada en la dis-
tribuci6n de momentos. El caso de un apoyo en cantilever es igual a1 de
de una mitnsula, como hemos dicho.
El crilcztlo de un po'vtico con nudos rigidos ( n o desplazables) se eiectfia mediante
un esqueina (vease fig. 3 a ) y consta de las siguientes etapas:
1. Se calculan para el tip0 de carga supuesto, 10s momentos de enipotraniiento
perfecto en 10s extrenios de las barras Miky se anotan encima de las correspondientes
barras del esquema.
Sumando en cada nudo estos momentos de empotramiento, obtenemos 10s va-
lores de 10s nionientos de sujeci6n para cada uno de dichos nudos,
10s cuales anotanios en el centro del circulo de cada nudo

20. 2. Obtenenlos luego 10s valores de 10s coeficientes de ~,epavticici)t o factoves de
givo p, repartiendo el valor /- & proporcionalmente en cada nudo a 10s valores
2 1
de las rigideces h' de las barras que concurren en el .Por ejemplo, para el
extremo i de la barra i-k tendriamos:
0)
rZnotamos estos valores en cada nudo frente a la barra correspondiente (dentro
de la superficie anular) y coniproban~osque su suma en cada nudo sea igual 3
3 Las sucesiz~asSnflz4enczns del givo de 10s U L I ~ ~ O Sa 10s momentos las de-
terminamos por iteraciones de la operacion
siguiendo de un nudo a otro, basta obtener la aprosimacion deseada
-
4. Sunlando 10s momzntos de ernpotramierrto en los extveinos rle las barvus MSk
con la influencia de 10s giros, obtenenlos 10s momentos definitivos de 10s extrenios
de cada barra. Asi para un estrenlo de la barra i-k obtenemos

21. 111. Pórtico de varios pisos
con nudos desplazables, en sentido horizontal
Cuando los ~iudosde una estructura durante su deformación, además
de girar se desplazan de su posición, véase figura 1, puede descompo-
nerse la deforniación de la barra vertical corres-
pondiente, así:
-L dJ
1. La barra i- k se deforma sin girar sus
extremos ni desplazarse (empotramiento perfecto).
2. El extremo i gira en un ángulo T~ sin girar
el otro extremo k, ni desplazarse ninguno de ellos.
3. El extremo k gira en un ángulo T, sin
girar el i, y sin desplazarse ninguno de los dos.
1. Los extremos i- k se desplazan entre ellos
en un valor 6 (véase fig. 4), sin que dichos extre-
mos experimenten ningún nuevo giro.
Teniendo en cuenta que estas tres primeras
etapas son exactamente iguales a las consideradas
en el caso de estructuras con nudos fijos (igual-
dad l), bastará para el cálculo del momento M,,
en el extremo de la barra que se desplaza, agregar
a aquella igualdad el valor M",, debido al despla- BIG. 4
zamiento 6, del extremo i de la barra.
Conocidos, por lo tanto, estos cuatro valores de los momentos en el
extremo de la barra, puede obtenerse el momento total resultante mediante
la suma:
ill,, = , v , k + 2 4 M',, A ( 1 a)
El valor M",, debido al desplazamiento del extremo de la barra lo desig-
naremos como la influencia del desplazamiento de los pisos de la estructura

22. sobre los nionientos en los nudos. Escribiremos de nuevo la ecuacióil de
equilibrio de momentos eil un nudo i
Z -TIlk=
(4
y mediante la ecuación (1 a) deduciremos la regla operatoria para el cálculo
de las influencias del giro de los nudos, igual que heiilos hecho en el caso de
nudos intraslacionalesi.
Empleando los niismos coeficientes de reparto aiiteriores, obtendre-
mos también ahora las influencias del giro de los niidos, niediante la suma
de momentos de sujeción *vi,de las iilfluencias de los giros de los estre-
mos opuestos y además de las influeiicias del desplazainieiito -11 ,, eii cada
una de las barras concurrentes en el nudo, es decir, de la suma
-.
JI,- Z 131'k, - 31",kl
(1 1
Para las barras de sección constante como supoilemos hasta ahora,
tenemos M",, = M",, . Por lo cual será necesario, debido a la simetría
del cálculo, un solo valor para la influencia del desplazamiento, el cual
anotaremos en la mitad de la barra.
Teniendo en cuenta las condiciones de eqiiilibrio de la estructura,
emplearemos para el cálculo de las iilfluencias del desplazamiento un
proceso análogo al utilizado para las influencias de los giros. Como luego
demostraremos, existe una conipleta analogía entre los dos procedimieiitos.
Consideraremos en este estudio, solamente pórticos de varios pisos coi1
columnas verticales, y para el cálculo de los desplazamientos horizontales
distinguiremos sucesivamente el caso de que actúen o no fuerzas horizon-
tales sobre el pórtico, y el caso de pórticos con columnas de distinta altura
en un mismo piso.
Corten~oshorizontalmente, figura 5,todas las coluninas de u11 piso r
cualquiera. Para que exista equilibrio, debe verificarse que la suma de
todas las fuerzas cortantes de las columnas de este piso sea igual a cero.
Esta ecuación de equilibrio, que debe cumplirse para cada piso (cuando
existe la posibilidad de desplazamientos horizontales de los iludos), se
' Siistitu~endola ecuaci:>n (1 n i en la de equilibrio
2 .ll,+ =: O
01
para u11 iiudo cualquiera i, nhtendre!nos

23. deduce del desplazamiento horizontal igual y contrario de las barras hori-
zontales, y mediante la misma pueden calcularse las influencias de los des-
plazamientos de los nudos para la obtención de los momentos.
Suporiiendo primero el caso de un piso r con co1umna.s de i.gual longitzhd,
obtendremos la ecuación de equilibrio, mediante la sustitución del valor del
esfuerzo cortante en la columna i-k, en la ecuación (1 a).
.Uik A- *Tíki
C'%,$= -
--
/lik
2 Ork= - '2 ( 2~lf',~- - -11 ' i k ~ : !~ f l ' ~ ~ ~ . $ l ' ~ ~ fA l f r k , ) = O
( 7 ) h'k Ifl
y de ésta
3
.rAll",k= -- - .r ( . f l ' c k +
( 7 ) 2 ( 7 )
La suma de las influencias de los desplazamientos
de las colurnnas de un piso r sobre los momentos,
puede determinarse, por lo tanto, mediante las influen-
cias de los giros de los extremos de las columnas del
misn~opiso.
I,a reparticibn proporcional de esta suma en las
distintas columnas, la deducirenios del siguiente razo-
ilamiento: FIG.5
Al desplazarse un piso r, la viga superior que une
las cabezas de las columnas en un valor 6, respecto
a la inferior que une los pies de las mismas, todas las colunlnas de este
piso se desplazan transversalniente en la misma cantidad.
Se supone, conlo siempre. que las longitudes de las barras son constan-
tes. Teniendo en cuenta que la influencia del desplazamiento depende
K
íinicamente del valor 0 de dicho desplazamiento y de los valores de -
h
?- es, además, proporcional a ellosR, se calcularán las influencias sobre
las coluninas del desplazamiento 6 del piso Y, en proporción a los valores
K
de - y teniendo en cuenta, además, que las columnas de este piso tienen
h
la misnia longitud, en proporcicíil a las rigideces K de estas barras.
--
a 1<1valor dcl momento debido al desplazaniieiito es
r n la cual 6 es el desplazamiento horizontal de los extremos de las columna: y h la longitud de las
mismas.

24. 2- P O R T I C O S DE 1,,7.4R I O S P I S O S
Para facilidad del cálculo, adoptaremos análogamente a los factores
de repartición, unos factores de corrivziento (o coeficientes de desplazamiento)
proporcioi~almente a las rigideces K de lasrepartiendo el valor - -
columnas del piso Y . 2
Llegaremos a la conclusión de que el cálculo de las influencias del
desplazamiento es tan sencillo como el de las influencias de los giros:
Sii~~zaremoslas inflztencias de los giros efz todos los extremos de las co-
lu~iznasdel piso, nzztltiplicaremos esta sztma sucesivamente por los factores
de corritllien to, obtenielldo de esta forma las inflztencias correspondientes al
desplazanzien fo.
Mediante las influencias de los giros se calculan las de los desplaza-
mientos y con éstas otra vez las de los giros en sucesivas iteraciones, hasta
obtener el grado de aproximacih deseado.
Ejemplo
Conlo demostracion practica de esta teoría, vamos a desarrollar el
mismo ejemplo de la figura 3 pero suponiendo los nudos desplazables.
Se conserva11 los mismos valores de los coeficientes de repartición
y momentos de empotramiento perfecto en los extremos de las barras (véase
figura 6 a). La primera iteración de las influencias del giro es también
exactamente la misma, ya que empezamos asimismo coi1 valores de la
influencia del desplazamiento iguales a cero, por no coiiocer otros más
aprosiniados. Anotamos los factores del corriniiento en el lado izquierdo
central de cada columna a que corresponden. El reparto de este valor
J
- - para el piso superior da lugar a un valor en cada una igual a -(),SO.
'L
En el piso intermedio hay cuatro columnas de la rnis~narigidez K. El
3
reparto del coeficiente - - en cada una de ellas da un valor de -0,37.5.
2
En el piso inferior, las coluninas iio tienen la misma rigidez, por lo
cual sumanios los valores de K:
0,2 + 0,2 -- 0,3 10,3 = 1 , 0
3
y repartimos el valor --, proporcioiialmente a los valores de K, que
2
para las colunlnas de la izquierda da:
y para las dos de la derecha
3 0,8 --- - 0,450
2 1 , o

25. elouaqui?
uo!slila~!eluacoqua!rrr~ze~dsapsolEsep!qapse1u?!qu~qEquansua
aslauaqrraqap'sopnusolapsol!Zsolaps-e!suangu!SEJl-elnsps1~
.olnslyslaE~O~E
soruanuytoa.(E'2hjasli?,luo!swaurnuEJE~EC~)01ñ6'8sopnusolua
sEuuInlosSEIapoqua!ur~z~ldsapIapsE!suanIp!SEIop-elrw~~su~d~yas
anbapsaqui?'uq!selaqlelaslaqeleqseyopeZaI1BYasvgerna!~BIu3
CZS37gVZV7dS3ClSO(I.9.V.Y03SOSIdSOIX6'113Cl03ILXQd

26. Para el nudo 10 la suma de influencias nos da:
+ 3,211 + 1,01 + 0 , 0 3 - 1,08 + 0,00 + 0,42 + 0.39 = + 0,97
Multiplicando este valor por los coeficientes de reparto, se obtienen
las correspondieiltes influencias: -0,?O, -- 0,03, -0,20 y -0,05, las cuales
anotamos como nuevas aproximacioiles en el iludo 10.
Para el siguiente iiudo 8, obtenemos como suma de influencias:
-2,10 + 0,04 + 1,26 C 0,00 ,0,42 i 0,2B = -0,12
1,a cual multiplicada por los correspondientes coeficientes de reparto,
da los valores: +0,02, +0,17 y +0,02, los que se anotaxi en el lugar
correspondiente del esquema.
Para el iludo 9 obtenemos:
-6,20 +0,17 + 0.16-0.20+0.00 k 0 , 4 2 + 0 , 2 6 = - 5.39
y como influencias de los giros: +1,30, +0,17, +1,04, +0,17.
A continuación, calculanios la influencia del desplazamiento de las
columnas.
Para el giro superior, deberenios sumar las influencias de giro de las
cabezas de todas las columnas de este piso
-n,o-l -k o,o2 + 0,24 + 0,08--0,5~ -- 0,02 = - o , ~ - I
Multiplicando este valor por los factores de corrimiento, obtenemos
para las tres columnas el valor 0,12 que es igual al de la anterior iteración.
I,a suma en el piso intermedio es
0,O-l + 0,02 + 0,lB + 0,17 4 0,03-0,03 -- 0 . 8 4 - 0,6S :- l,13
que multiplicado por el factor de corrimiento -0,975, rios da el mismo
valor anterior igual a +0,42.
En el piso inferior, la suma de las influencias de giro da
+ 0,02 + 0,17 -0,05- 1,02 = - 0,88.
JIultiplicando por los correspoildientes factores de corrimie~lto,nos da,
para las columnas de la izquierda, una influeilcia de desplazamiento igual
a +0,26 y para las de la derecha, igual a f 0,40.
La cuarta iteración da lugar solamente a pequeñas correccioxies, cuan-
do no se precisan más que dos decimales, y en realidad sólo será conve-
niente hacerla en los nudos 1, 2 y 3 y eventualmente en el l.
La correccióti de errores que, según hemos explicado, se obtiene para
el cálculo con nudos fijos, puede también aplicarse al caso de nudos des- ?
plazables. Por lo tanto, cuando estamos seguros de no haber cometido
error en el cálculo de los momeiltos de sujeción. de los coeficierites de
reparto y de los factores de corrimiento, podemos estar seguros de obtener
resultados correctos.
La comprobación de los resultados de un cálculo es a veces laboriosa,
pero siempre es recomendable cuando se han debido realizar gran nú-
mero de operaciones; es además muy conveniente, antes de continuar un
cálculo, la comprobación de los resultados ailteriores.

27. Obtenidos las influencias de los giros de los nudos y de los desplaza-
mientos de los mismos, basta para obtener los momentos definitivos en
los extrenlos de las barras, aplicar la fórmula (1 a) en la cual se suma
en cada estreirio de la barra:
el momento de empotraniierito perfecto,
la doble influencia del giro del m i s m o nliilo,
la iiifluencia del giro del f~ridoofl~~esfoy
la influencia del desplazamiento.

28. Para calcular los momentos definitivos en los extremos de las barras
del ejemplo que estamos desarrollando, en el cual hemos obtenido las in-
fluencias de los giros y de los desplazamientos, el procedimiento a seguir
es el siguiente:
1. Se tachan en cada extremo de barra los valores no utilizables,
dejando solamente los momentos de empotramiento perfecto y la influen-
cia final del giro (KkY Mfik).
2. Se forma en cada barra la suma de las influencias de giro en
ambos extremos más la del desplazamiento (Mi, + M',, + M''$. Esta
suma se anota en ambos extremos de l a barra.
3. Se suman estos valores anotados. (En las barras horizontales
tenemos en cada extremo tres valores, y en las columnas dos, ya que en
ellas no existen, en este ejemplo, momentos de empotramiento.)
La suma de estos valores es el momento total, como podemos obser-
var comparándole con la fórmula (1a). Los momentos resultantes se han
dibujado en la figura 6 b. (En el siguiente ejemplo, en la figura 8 b, ex-
plicaremos además el cálculo de los momentos flectores definitivos.) De-
bajo de los momentos totales obtenidos en el extremo de cada barra, ano-
tamos entre paréntesis los valores obtenidos en el caso de nudos fijos
(obtenidos en la fig. 3 b). Esto nos permite comparar estos valores y darnos
cuenta de las diferencias, especialmente en las columnas; incluso hemos
obtenido cambios en el signo de los momentos.
Vista la sencillez del cálculo para el caso de nudos desplazables, no
está justificado el suponer que estos nudos son indesplazables, como he-
mos hecho antes.
Cuando hay articulaciones en los pies de las columnas, en lugar de
empotramiento como en el caso anterior, se puede efectuar el cálculo
partiendo también de los momentos de empotramiento perfecto en los
extremos de las barras, pero asignando un valor a la rigidez
3 1K' = -- .-
4 1
para las barras que tengan uno de los extremos articulados.
Los factores de corrimiento de las columnas, en el caso de articu-
lación en sus apoyos, siendo todas de la misma altura, se obtiene repar-
tiendo el valor (- 2) (como luego demostraremos) en lugar de
(- %l.proporcionalmente a las rigideces K de dichas columnas.

29. P 6 R r I C O DE V A R I O S P I S O S C O Y SC'DOS D E S P L A Z A O L E 27
En el caso del pórtico de varios pisos, sobre el cual actúan fuerzas
horizontales en los nudos o fuera de ellos (véase fig. 7), no podemos con-
siderar estos nudos como rígidos. Existirán ahora, además de los rno-
mentos de sujeción, unas fuerzas horizontales de fijación (representadas
en la fig. 7 por los valores p)que impidan el desplazalniento de los nudos,
como los mometitos inipideii el giro de los mismos.
Calculados los momentos de empotramieiitc perfecto en los extremos
de las barras, se calculan luego los momentos de sujeción, así como las
fuerzas de fijación mediante las eciiaciones de equilibrio.
Para calcular los desplazamientos en la misma fortna que lo hemos
liecho para el caso de cargas verticales, deberemos sólo tener en cuenta
que ahora intervendrán unas fuerzas de fijación H que antes no existían.
Estas fuerzas las podremos eliminar introduciendo, para cada una de
ellas, una igual y contraria que la anule. Estas fuerzas adicionales se repre-
sentan en la figura 7 a. Efectuando un corte horizoiital para todas las
columnas de un piso cualquiera Y, podemos establecer la condición de
equilibrio:
( 1 )
'Y Qtk = 'Y H ,
(1) Z - 1
O sea, que la suma de las fuerzas cortantes en todas las columnas del
piso Y es igual a la suma de las fuerzas horizontales H que actúan en los

30. 28 P 6 R T I C O . S D E V A R I O S PI.O.s'
nudos por encima del piso r. Esta swna de las juerzas H de lijacio'n gzie actzían
por encima riel piso r la designaremos como es/tterzo cortante Q, bajo este piso.
Las fuerzas cortantes de un piso pueden obteiierse de las fuerzas
de fijación para el caso de empotramiento perfecto. Así, por ejemplo,
calculando la fuerza cortante Q,, para una columna i-k del piso r , y usando
luego la fórmula (1a ) , teniendo en cuenta que
y que todas las columnas del piso tienen la misma longitud h,, podenios
poner
y para la suma de las influencias del desplazamiento en todas las colun~rias
del piso r:
1.%f",,= -
( 7 ) 2 (rl
Q, .hrDesignando como momento del piso M, el valor -- igual al tercio
3
del producto del esfuerzo cortante por la altura del piso, teiidrenios:
- Q, . 11,
.TZr= --
3
1,os factores de corrimiento son iguales a los del caso de carga ver-
tical, y la única diferencia con este caso consiste en que al hacer la suma
de las influencias de los giros en'los extremos de las colunlnas debe aña-
dirse adeniás el nioniento del piso ur.
El cálculo, por lo tanto, de un pórtico de varios pisos coi1 cargas hori-
zontales coiistará de las siguientes fases:
1. Cálculo de los nlonlentos de empotraniiento perfecto eil los estre-
mos de las barras y de los momentos y fuerzas horizoiitales <le sujeción.
2. Cálculo de las influencias de los giros de los iiudos y del despla-
zamiento de los mismos, empezando coi1 los momentos de sujeción, igual
que para el caso de carga vertical.
3. Cálculo de los esfuerzos cortantes en los pisos y de los monientos
de piso M,, debidos a las fuerzas de sujeción. (Para los valores de estas
fuerzas horizontales de equilibrio se calculan también las influencias de
giro y desplazamiento de los nudos, por medio de estos momentos de piso
M, y se suman a las indicadas en la fase U.)
Las operaciones a realizar en las fases 2 y 3 pueden serlo al inismo
tiempo para las influencias del giro y del desplazamiento.

31. L a difere~lciaesencial entre el cálcztlo de un pórtico de varios pisos con
carga horizontal, y otro con cargas ~!erticales,consiste en que al calcular la in-
flzlencia del desPlazamiento debe agregarse en los extremos de las colltmnas
el momento del piso %,.
Designando por v,, el factor de corrimiento de la barra i-k, el ~ralorque
nos da los momentos debidos a1 corrin7ienfo es:
El valor que da los monieritos debiaos a la influencia del giro del nudo
es designando coi1 ,ui,el coeficiente de giro en el extrenio i de la barra i-k:
Coniparaiido estas dos igualdades, vemos la analogía de las inismas.
En ambos casos, en lugar de M',, hay AV",k;en lugar del factor de giro,
el factor de corrimiento, y en lugar del momento de sujecióii, el momento
del ~ i s o .
Tanibiéii es análoga la semejanza geométrica.
Por la rotacióii del nudo giran todos los extremos de las barras en el
niisnio árigulo t y las influericias del giro, debidas a esta rotación, son
proporcionales a las rigideces K de las barras.
La determinación de la influencia del desplazamiento se lia obtenido
calculando el niovimiento de las vigas entre sí. Las columnas del piso
considerado experimentan, por lo tanto, el mismo desplazamiento trans-
versal 6, y, por ello, su influencia sobre los momentos de los nudos debe
estar en relación con las rigideces K de las barras.
Debemos tener en cuenta, además, que al considerar el desplazamiento
de los nudos su influencia aumenta en proporción al número de pisos más
el número de nudos de cada piso.
El cálculo, por lo tanto, de un pórtico de varios pisos con carga ho-
rizontal consistirá en:
1. Suposición de empotramiento perfecto, cálculo de los momentos de
empotramiento en los extremos de las barras, de los momentos de suje-
ción, de las fuerzas de fijación y mediante ellas, de los esfuerzos cortantes
y momentos de piso
(Los momentos de piso son positivos cuando la carga horizontal actúa de
izquierda a derecha, o sea cuando las fuerzas de fijación lo son de dere-
cha a izquierda.) Deben anotarse los momentos de piso, en el esquema,
a la izquierda de la columna del piso correspondiente.
2. Los valores de los factores de giro y de corrimiento son los mismos
que eii el caso de carga vertical (véase fig. 6 a).

32. :(O P(íKTIC0S DE I/'dRIOS PISOS
3. A1 efectuar la primera iteración debe tenerse ya en cuenta, en
cada nudo, el momento del piso M,,en lo cual se diferencia este cálculo
del caso de carga solamente vertical. Después de cada iteración en todos
los nudos, se hace la compensación por pisos de los valores encontrados
en cada extremo de las columnas de un piso y se alternan las dos operacio-
nes hasta conseguir la aproximación deseada.
3. El cálculo de los momentos totales es igual al caso de cargas ver-
ticales, pero col1 desplazamiento horizontal de los nudos. En el siguiente
capítul'o se explicará un ejemplo de cálculo con carga horizontal.
Para el caso de actuar a la vez los dos tipos de cargas verticales y
horizontales, el cálculo no ofrece ninguna nueva dificultad, siguiendo la
marcha indicada anteriormente.
LOLVMXAS D E DIFERENTE ALTURA E N UN MISMO PISO
La existencia de columnas de diferente altura en un piso Y no modi-
fica los valores de los factores de giro y las influencias de dichos giros,
solamente las influencias del desplazamiento experimentan variación.
Empezanlos eligiendo conlo longitud de las columnas del piso Y un valor
ficticio Iz,, igual al de las columnas que figuran en tnayor número con esta
longitud.
Escribamos de nuevo la condición de equilibrio,
que debe cumplirse en cada piso Y, la cual puede transformarse teniendo
en cuenta la ecuación ( l ) , y multiplicando luego por h,, en la siguiente:
y llamando factor de redz~cciónel valor c:
obtendren~osiiltroduciendo, además, el valor 2, del momento del piso,
establecido anteriormente
Al desplazarse transversalmente un piso Y, es evidente que todas las
cabezas de las columnas se desplazan en un mismo valor 6. Las influencias

33. P ~ R T I C OD E V A R I O S PISOS C O N N U D O S L)ESPLdZABLES 31
del desplazamiento dependen, por lo tanto, únicamente de 6 y de la relación
Kik--
hrk
y son proporcionales a estos dos valores. Teniendo en cuenta, además,
que el valor 6 es igual para todas las columnas del mismo piso, la influencia
del desplazamiento será proporcional a
Kik
o también, el valor cik Kik,resultando de ello la relación
y expresando el valor del factor de corrimiento en una forma general,
obtenemos
y la igiialdad (5a) que expresa el valor del momento total debido al des-
plazamiento, puede escribirse así:
O sea que, para pisos coi1 columnas de distintas alturas, debemos tener
en cuenta las siguientes n~odificaciones:Empezaremos tornando una altura
de piso h, en la forina que hemos indicado; calcularemos para cada columna
hlel factor de reducción c = - y lo anotaremos al lado de las mismas.
h
Los factores de corrimiento los calcularemos mediante la igualdad
(4' aj y los anotaremos también en el esquema de cálculo. Al terminar
con la influencia del desplazamiento, niultiplicaremos la suma de los mo-
mentos de las influencias del giro en los extremos de las columnas, por el
correspondiente factor de reducción c.
En el caso de columnas de igual longitud, efectuábamos la compro-
bación de los factores de corriniiento, viendo si la sunia de los mismos en
cada piso era igual a --
( 5).Para el caso de columnas desiguales, deberá ser la suma del producto

34. Vamos a aplicar 10 dicho, al esquema indicado en la figura 8, el cual
difiere de la estructura de la figura 3 únicamente en las longitudes de las
dos últimas columnas del piso inferior.
Los factores de giro y de corrin~ientoson los mismos calculados
antes. Elegiremos como altura ficticia para las columnas del piso inferior
h, = 6,00 in, con 10 cual los factores de reducción serdn para este piso:
c = 1 para las dos colun~nasa la izquierda
h, 6,00
C = - = - - - l,50 para las dos de la derecha
h,, 4,00
Los factores de corrimiento para las dos columnas de la izquierda de
este piso inferior serán, según (4' a)
y para las de la derecha
la comprobación de los valores de los factores de corrimiento da:
2 (-0,171 . 1,0 -0,386. 1,50) = - 1,500
En el esquema de la figura 8 a, anotamos los factores de giro, factores
de corrimiento, y en las columnas del piso inferior, además de los facto-
res de corrimiento, los de reducción c.

35. $U11S'(]-
ZI--I'vJt.= -
i0C't'.C'O-Ilt'-
:epla!nbz?t.E~Jelaru
-ude1apseurrIn1osse1enclosesalsarraualsrxa019sanb'selleqse1apsoru
-aqxaso1uao)ua!rueqodruaapsoluaruoruso1sorue~oueugsenuguosy

36. 35 P Ó R T I C O S L)E V S R I O S PISOS
Para evitar confusiones, conviene separar estos momentos de empotra-
miento en los extremos de las columnas anotados en el esquema, mediante
una línea horizontal por debajo de los mismos que los separe de las influen-
cias de los giros, que se obtendrán más tarde. (Así lo haremos en fig. 8 u.)
A continuación se anotan los momentos de fijación obtenidos por suma de
los momentos de einpotramierito, en el centro del círcrilo de cada nudo.
Sigue luego el cálculo de los momentos de los pisos. Para ello precisa-
mos primero los valores de las fuerzas de fijación, que son, designando
la viga superior con 1,la intermedia con 11y la inferior con 111:
Estas fuerzas serán positivas, según la regla de signos adoptada, por
actuar de derecha a izquierda (la carga actúa de izquierda a derecha).
Con los valores de las fuerzas de fijación, obtenemos las fuerzas cor-
tantes del piso (que también son positivas) así:
en piso superior Q = 0,875t
en piso intermedio Q = 0,875 -+1,875-2,750 t
en piso inferior Q = 0,875 + 1,875 -+2,500 == 5,250t
y los momentos de los pisos:
-t1,021 nit
Anotamos en el esquema, a la izquierda de las columnas de la pri-
mera fila, estos valores de los momentos de los pisos (dentro de unos
recuadros para mayor claridad) y a continuación empezamos con el cálculo
de las influencias del desplazamiento, que son mayores que las debidas
a los giros.
Como no conocenios, hasta ahora, ningún valor aproximado para estas
influencias de los giros, calculamos únicamente las influencias del despla-

37. I - ' ~ R T I C ODE V ARIOS P I S O S CO.V N U D O S DESPLAZA RLES 35
zamiento, n~ultiplicandolos momentos de los pisos por el correspondiente
factor de corrimiento, obteniendo para las columnas del
piso superior . . . . . . . . . . . . . . . . . . . . . 1,012 . (-0,500) = --0,sl
piso intermedio . . . . . . . . . . . . . . . . . . . 3,666 . (- 0,375) = -!,38
piso inferior, dos columnas izquierda. 10,50 . (-0,171) = -- 1,80
piso inferior, dos columnas derecha .. 10,50 . (-0,386) = -4,06
Anotamos estos valores en el esquema (fig. 8 a).
A continuación, calculamos las influencias de los giros en la forma
conocida, y seguimos el cálculo hasta la segunda iteración para cada uno
de los ntidos. Como demostración de las desigualdades que aparecen'en las
colutnnas del piso inferior, continuarenios el cálculo hasta la tercera ite-
ración.
Para la influencia del desplazamiento, calcularemos las del giro, para
el piso superior:
y como influencia en el piso: -- 0,500 . 1,14 = 0 , 5 7 para las tres columnas.
En el piso intermedio, como influencia del giro:
+ 3,67 + 0,10 + 0,12 + 0.04 + 0,06 + 6,05 + 0,13 -k 0,09 +0,30 = + 4,56
y las del desplazamiento -0,373 - 4,56 = -1,71 para !as cuatro columnas.
En el piso inferior, con columnas desiguales, debemos mtiltiplicar por
el factor de reducción c:
-E 10,56 + (0,12 -+ 0,06) . 1,OO + (0,20 + 0,45) . l,50 = $- 1l,66
y las del desplazamiento para las
dos columnas de la izquierda -0,171 11,66 -=-1,99
dos columnas de la derecha -0,386 . 11,66 = -4,50
A continuación, repetimos las iiifluencias del giro en nudo 1:
+ 0,51 + 0,11 + 0,05 -0,557 = -+ 0,10 ~ t c .
Para obtener los valores totales de los momentos flectores, repetimos,
para mayor claridad, el esquema en la figura 8 h. Transcribimos en ella
los valores de los niomentos de empotramiento en los extremos de las
barras y debajo de ellos los valores finales, obtenidos para las influencias

38. del giro y del desplazainieilto. Comparaiido con la figura 8 a, venios que
ya en la seguilda iteración, los valores obtenidos diferían muy poco de los
finales. clue anotamos en la figura 8 6. A continuacióri y en el extrenio
de cada barra sumamos estos valores, poniendo una línea horizontal por
debajo de ellos, cuya sunia 110s da los moliientos totales en los estremos.
Puede también operarse, sGlo con el esquema 8 a, tachando todos los
valores que no necesitanios y sumando los momentos de empotramiento
perfecto con los de las influe~iciasde la íiltitna iteración.

39. PÓRTICO DE V A R I O S PISO.5 C O S S U P O S DESPLAZA BLES
Supongamos ahora que en el piso inferior con columnas de diferente
altura hay alguna de ellas articulada en el apoyo.
Una columna articulada en su base que tiene un coeficiente de rigi-
dez K y una longitud h, experimentará en su extremo superior un giro t
y un desplazamiento horizontal 6, iguales a los de una columna empotrada
3 3
en su base que tuviera una rigidez K' = - K y una longitud h' = - h.
4 2
Podemos sustituir, por lo tanto, las columnas articuladas en su apoyo,
por otras empotradas, teniendo en cuenta los valores anotados. Solamente
debemos tener en cuenta el nuevo valor del esfuerzo cortante en la columna
articulada, por lo cual escribiremos la igualdad, que nos da el valor de esta
fuerza cortante
3
y en ella torriaremos para valor de m = -, en el caso de columna articu-
4
lada y m = 1 para ei caso de empotramiento.
El procedimiento a seguir será, por lo tanto, el siguiente: calcularemos
primero los momentos de empotramiento en los extremos de todas las
barras de la estructura, y para aquellas que estén articuladas sustituiremos
3 3
los valores de la rigidez K y longitud h por otros K' = - K y h' = - h.
1 2
Con estos valores, calcularemos los factores de giro como es costumbre, y
los factores de corrimiento mediante la fórmula:
hr
en la cual c,, = - es el factor de reducción de la columna y el valor de
h i k
3
nz = - o bien m = 1, según sean articuladas o empotradas.
4
Para la comprobación de la suma de los factores de corrimiento del
piso r, emplearemos la fórmula

40. 38 I ' f i h ' I ' I ( OS DI; 1.ARIO.S P I S O S
Ciiando todas las colutiinas del piso r estáii articuladas en sil apoyo,
J
sustituyerido el valor i l z = --, obtendremos para el valor de los factores
4
de corrirriierito en este piso:
y su comprobació~cori
REsrram~DEL CAPÍTYI.~111
El cáiciili de los nionieritos totales para uri pjrtico de varios pisos cori niidos
desplazables, se desarrolia de la forilra sipi~ittitey iiiediatite ei es<;uciiiade la figura 8 a
1. Sr ca::i113:1 p:iii~:.i<: los iiionieiitos de eniputraiiiieiito perfecto iv,b eii el
extí-c:r;o í!: c:L<!~:1>3?1:1, ianls [lar2 ias fuerzas rerticales coiiio irut~zoritnles- sc aiio-
iai: etl 10.: extrenio:. <!c las uiis:iias.
F>c~)i,iieric-~i,i~:cgo, loa trioiiiciito~dc siijecicíii cii rarix iiiicio i, siii~~:iiitiolos
31011;~iit~7:UL. em~<ikla~illí~itii<o;-respondientcs a los estreiiios Sic l~is1)nrras (1nv
coiír~~:iici,eri ei riudc i
,vi~ Y Z2 .G-;k
(il
y ioi; a:io:atiics el: e' ccritro de los rirciilos de cada iiccio.
ZI",el cas<; di.ex; ."
-.
.>,ir cargas horizoiitales, clcteriiiinarenios a(2ciii:ís las fuerzas
¿!e fij:.cií!;; ií > coíi ei!a~.,cr. caca 1)iso1 , la fuerza (?, uiediante la siiiiin de estas fiicr--.-
za- 1< qii:, :;iLi1zi, pi:r ei.,ciin~(iei ~lisoconsiderado
--
cOí eSrC.:,, v,91s.r<J~.,.*.4 i~F~:cndreizioclos ii:oriieiitos de piso .Ir - (2, -11, -, los ciiaies
3
ariotzreiii<.i; a lc izqi~icrdnde las co:uniiias de la priiuera fila, deiitro [le uir reciia<iro.
2. CGteritlrciiro: ioc cclr/i~icntrsiif ~rpar,toj; (igual coiiio eu e! caso tic pórtico
1
de niidos fijo:;) repariiciido ei vztlor - 'eii ci?ila iiu<lo, ~)ro!~orcioiialii:<~iitt:n las
1
rigideces li de lac. barras c l u ~co:Iciii.tcti eri el tiiisiiio. Así para el estrciiio z tlc la
barrá 2 4 , teiierl~oc.

41. PÓKTICO DE lrARIOS PISOS COK NUDOS DESPI.AZARLE.5 39
Después de anotar los valores de los coeficientes de reparto en cada nudo frente
a la barra respectiva, comprobaremos que la suma de eiios es en cada nudo
1
igual - :
2 1
z@;A == -- - (comprobación)
íi) 2
Ca!ciilarernos luego los /actores d~ corrimiento v, distribuyeiido en cada piso el
valor (- f proporcionalniente a las rigideces de lar columnas y 1% anotarenios
a !a izquierda dc la colu~utiscor~ecpondiente.Tiara uno columna i-k del piso r , el va-
lor de a, será.
3 K,i;
l'ik = - - ---
2 CK,h
(4 a)
(71
la suma de :os factores de corrimiento scth en cada pije igual a
3. Lar in/iiiz>i:ias dri givo AlfiR se oY~:eirdrAi? por itcraiihr; sucesiva de la
fórmula: -
M';,,=-. l l i b L11.1; -i Z1 4 ( 3 a)
( L j,-,
de iinc: a otro nu.do
Las ir,,/iu~,;ciasd?l n'~sfila?a;iiie~zloJT.~'',~, si. ob!e:iidiA;.i p ~ :itc~nciór;c:irczira a
todos los riiidol; d- la lóruiulo
1,as iteraciorre~riiediantc las fórinitlac (3a ) y (5 nj i;?,iali snr<~:..iv::s aitenia?id-,
1az dos, t'ilipczalicli? coi- 1:i (3a) para cada riudo y liic~cj1á (S n ) ctr.., liwtt. qiie
toda? la? i r l f i u ~ i ~ i *di. la.",giros y decplnz~iriilritai!Icguíli a !rc cs;ict ¡ti16 tleiinda.
4 Obte~idrt:iios1x7 iiii los i j i ~ ~ i ~ ~ l í f o . ;ci'eji~;i(i?~oscí; i c ~tnt~.~ri.r,.s26 lns liarrcis,-.
suiiiandí, los rnorileiitos iir: ci~;~iotraiiUe;i!o las ini'liic.riri-15iic 10:- gito:: ;l:'ik,y
las itlfl~iericias[le! dcsplaza~iiii.iitoM",i, h í , por ejciii!,lo, Ila?a c.¡ t:xt:erilr, dc 1::
barra i-k -.
.lí'::: ;:= ' V , h 4- 2!Lf'ik4 iVJk"-, '"i.T1stL, ii (1'
B. Las colic~:i?zasd: 117: I I C ~ S I + K I piso /ir))z~i.~ I / U Y U S iiisii?:!ns.
1. c1 cdlci.i!o rlc los t!:c~;te.rifosd t Jijución y ift los v:on:e1i.!as de los +isc;s es el
iuisxi~udt.1 caso dc pi,so; coi1 coliimnas tiT>igii..,! altiira. C:r>:no eltiira dfl fl.s.s h,
piiedc ioina?s-2 la lo!igliild de la-. colu!iinas que iigiirfli Cii ilia'.o? ~~lítilf-le.
2. Ir1 cá/cu!r, cie 1% /<;:lo,-es de gi;,o , ~ iy su coiiiprol,r:~:i es iyiiai. I'2it~1;, altura
adoptada de piso h,, calciiloreii~ospara cada colutiii1-7,i-.k dcl 1,is-;>r: lo' Iaciorei de
reducci6ii c:
h,C I A " '
hin
los cua!cs anotarenios a! laso de cada coluiiina ec el equclixa rZe chlculo (veefc la

42. figura 8 b piso inferior). I,os factores de corriniiento vik del piso Y los determinaremos
iiiediante la siguiente fórmula
(4 a')
y la comprobación con: -
3. El rálculo de las influencias del giro M f z k es igual al caso de pkos con co-
luinnas de la inisma longitud, es decir, mediante la fórmula (3 a).
La influencia del desplazainiento MIlk se calcularh iiiediarite la fóriiiula:
M",k = v , k [M, 2 c,k ( . ~ ' , k ~ f ' k , ) ] (5a')
4. El cálculo de los monieiitos definitivos en los extreiiios de las barras es el
rnisino que en los pisos con columnas de igual longitud, es decir, con la fórmula ( l n ) .
C. Pava el caso de colrwnnas avtzculadas en sus apoyos con una rigidez II' y una
longitud h se calcularán, ciespués de anotados los momentos de empotraniiento en
los extreiiios de las barras, sustitiiybndolas. por otras eriipotradas en sus bases con
3 3 3
una rigidez K' = -Ii', con una a!tura h' = - h y un coeficiente m - . Con
1 4 4
estos valores se obteridrdn los coeficientes de reparto v factores de corriiiiiento coino
lieiiios explicado en el capitulo correspondiente. 1,uego se seguirá por el método
corriente.

43. IV. Comprobación automática
de los momentos totales
Este niétodo de cálculo ofrece (con10 het-iios explicado al priiicipio)
una coiiiprobacicín autoniática del mismo, pues con excepción de los va-
lores fundatiientales, o sea, momento de rigidez, nionientos de los pisos y
rigideces K de las barras, el resto se cotnprueba por iteración.
Aunque para la corrección de los factores de giro y de corrimiento
existe una comprobación por sunia, es interesante u11método que permite,
adeiliás, coniprobar el resto de valores. Debemos hacer observar que eti
el caso de repaso por la misnin persona, de los cálculos efectuados, y si-
guiendo el niismo camino en el repaso que en el primer cálculo, puede
cometer siempre el i~iistiioerror, con lo cual este repaso no es conveniente.
I'ara los valores fundanientales, es decir los nlomentos de inercia,
longitudes de barras, rigideces K, etc., no puede seguirse otro método que
el corriente, por lo cual sólo es posible el repaso por otra persona o por la
misiiin, con gran cuidado. I'anios ahora a esponer u11 sistenia de compro-
lmción de los monientos definitivos con los datos primitil-os del cálculo.
Esta comprohacicín será satisfactoria cuaiido pueda deniostrarse que
eil ninguna parte de la estructura existe un desequilibrio o deformación
que sea incompatible con el estado de equilibrio de diclia estructura. Exis-
tiría esto, por ejemplo, cuando en un niido, la suma de los momentos defi-
nitivos sea diferente a cero, ya que en este caso existiría un momento
flector en el nudo que desequilibraría el tnismo, o también, cuando los
extremos de las barras que coticurren en un nudo no giraran todas en el
niistno ángulo.
Cuando en un pórtico de varios pisos no es posible el desplazamiento
de los nudos, basta coinprobar ias dos siguientes condiciones:
1. La condición de equilibrio se cumple cuando no necesitamos agre-
gar en ningún nudo de la estructura otras fuerzas (fuerzas de fijación o

44. 12 P Ó l i l l ( OS L)L' I..-lKl 0.5 P I S O S
momento de sujeción que no existen en reaiidad) para mantener el equi-
librio del iriismo.
Se debe tainbién comprobar que eii cada nudo la suma de los momen-
tos definitivos es igual a cero, o sea, cuando sobre el nudo actúa un rno-
niento exterior, que la suma de los monientos defiilitivos en este nudo es
igual al momento exterior.
11. La coiidición de que la deforinacióri es normal se cumple cuaiido
todos los extremos de las barras rígidamente unidas giran en e? rriismo
ángulo de giro.
La comprobación de las sumas de los monientos flect~resdcfiríitivos
(condición 1) se puede efectuar muy fácilmente. Para coniprobax 1s coii-
clición 11 deberetrios calcular los ángulos de giro en los extremos cie las
L* es.barras. Estos áiigulos se obtiefieri coilio suma de tres valores ptrc'71
Para el extremo i de la barra i-k el ángulo de giro se calcula por 12 ccaucióil
. .
ro,, es el valor del ángulo producidn pcx ia carga exterior a 1;; :-igs 2-Iz
~iiii~~lciiienteapoyada (un tramo sini~,lc con dos apoyos). T:I ~ ~ g i ~ ~ ~ c l
iiii.eni?)~c;es el valor del giro proclücido por el mon~entore~u1t;~~iit.c-en el
estrenlo i, y el te~ccrmiembro, el -:do; proclucido por eI i:ioni~i;t,, r e d -
tai~tcque r?ctíia c:i el otro extrenir? k . -, : .
I'ara i:iayor corriodidad de cálciilo, c:!lculareii~o~e;; l~:ga!-Cii :: LII-
golos de giro T, otro ángulo Ti c?bteiiicio's~~iuliiplica~idoT, l)oi :! ';'
y entonces
Afik 1 :Ilik?',* = SCik.+ - . -~
I,', !< .> Iiik
61 cA!cdo de estos ángulos de gJro es ii~uysencillo y se efcct:':: <'ii cl
i!!isiii~ esr1tie:n;i de la estructura. E I I I ~ ~ Z ~ I I I O ~determiiiatld~3pn;.~? 1:- wrga
cste~iorIns alo ores del giro de las barras iiiultiplicadoc pcr 3 i:: c: (:( cir,
Y'(!,,, nlediante datos de los matiu-iles y a~iotándoloeii el e,ique.!iici eil
los cstrenios de las barras correspoiidiciites. Calculareiilos li~ego~ I Rcada
ts?icriio de la barra 7 el valor de "" y lo anot.uenins taiiitiiiii el! el
Kik
esqueiiin. De acuerdo coi1 la ectiacióii qcc 110sda 7;, deberenios Cn;cntrí iite
Af$):
.-.r!IC Ct71l-di:.idir en dos partes iguales el valor de y ariotarlo con %;;.:S
h'i,
trario eti el otro extremo de la misma barra. 1,a suma de estos tres vnlores
determina eri cacla extremo de la barra el valor de T,, qtie l~:~~c:iii~o::.;y el
cusl para todas las barras que ccticwrei? en un nudo rígido delicii iei~cr
el iiiis:ilo valor.

45. C O I I ~ P R O B A C I O NDE L O S A I O h I E N T O S T O T A L E S
B. PÓRTICO DE VARIOS PISOS CON NUDOS DESPLAZABLES
EN SENTIDO HORIZONTAL
Cuando existe la posibilidad de desplazamiento horizontal de los nudos,
es necesario que se cumplan no solamente las condiciones 1 y 11,párrafo A,
sino también otra condición de equilibrio y otra debida a la deforniación:
1a . En un corte horizontal por todas las columnas de uri piso, la
suma de las componentes horizontales de la carga esterior actuando por
encima de esta sección debe ser igual a la suma de todas las fuerzas cor-
tantes eii las coluninas. (En caso de carga vertical la suma de estas fuerzas
cortantes es igual a cero.)
11o. El desplazaniieiito transversal 6 entre los extrernos de todas
las coluninas del mismo piso debe ser igual.
Hagamos en cada piso un corte liorizorital. Cuando la carga horizoiltal
actúa úiiicamente en los niidos es indiferente a qué altura del piso se efectúa
el corte. Pero cuando la carga liorizoiital actúa directamente sobre las colum-
iias, debe cciiisiderarse la coliimiia coiiio una viga libreniente apoyada en
aii-iboslados y calcular el ptiilto d t iiiflesióri, o de canibio de sigilo, de la
fiierza cortatite para la carga dada. Efectuaiido el corte liorizontal por estos
l3uiitos de fuerza cortante igual a cero, queda el esqueitia como en el caso de
carga úiiicaiiieiite en los iludos. Se suiliati despu6s todas las fuerzas horizon-
tales por exima de este plano y sii siinia debe ser igual a la siinia de las fuei-
zas cortantes en las columnas. Las fucrzas cortantes de las coluninas i-K qiie
están íiriicamrnte cargadas por trioiiieiitos eii sus extretiior-, cuando el corte
liorizoiital se ha liecho eii la foriná indicada, sc calcularáil con la ecuaci6ti
híái cóiiiodo qiie el eiiipleo de las fuerzas cortaiites tAscalcular con el
producto de la altura del piso h, por la fuerza cortante. Para las coluiiiiias de
lorigitiid igual a la altura del piso h, iio es iiecesario dividir por la altura del
i)iso, y tendrenlos: ii
- - , i ( + 1 . -2-
h , h
Par;i las coluiniias con 11,~= h, iiecesitaii~osíiiiicatiiciite sumar los
!iioiiieilt,)s ex los extremos.
I'zra uti corte horizoiital por uii piso r, doiidc todas las coluninas
tiene:i la misiiia longitud, la ecuacióii de equilibrio 1n puede escribirse
corno 13 suiiia de todas las conipone~iteshorizontales de las cargas que
r
actiiaii por encinia del corte del piso r y que se designa como .Z IPi
1

46. 44 PÚRTICO.5 DE V A R I O S P I S O S
L a condición de equilibrio 1a se cumple para el piso conszderadn.cuando la
suma de los momentos definitivos en los extremos de las columnas del piso r es
igual al producto con signo contrario de la altura del Piso h, Por la suma ZH,.
1
(Las fuerzas H son positivas cuando actúan de izquierda a derecha.)
Cuando las longitudes de las columnas del piso r son desiguales, la
condición 1a toma la forma siguiente:
Comprobación de las condiciones de deformación 11
Comparando con una estructura de nudos fijos, en el caso de nudos
desplazables horizohtalmente, debemos comprobar los ángulos de giro
en los extremos de las barras, teniendo en cuenta que no cnnocemos al
principio el valor del desplazamiento transversal 6 de las cabezas de las
colun~nascon respecto a los pies de las mismas. Así como la determinación
de los ángulos de giro eii los extremos de las barras horizontales se efectúa
igual que en el caso de nudos fijos, es necesario para las columnas deter-
minar primero los desplazamientos transversales 6. Es necesario, por 10
tanto, empezar con la comprobación de la condición 11a. El cálci.110 de los
ángulos de giro en los extremos de las columnas se diferencia en el caso
de nudos móviles del caso de nudos fijos, únicamente por la adición del
o
ángulo -, es decir, el ángulo que fornia el eje de la barra desplazada con
h
su posicion primitiva (el eje de la colunina es la recta de unión entre los
6
nudos). Llamaremos a este ángulo - ángulo de desplazamiento transversal.
h
El método explicado en los capítulos anteriores ofrece, además, en
el caso de comprobación una ventaja esencial, la de que los ángulos de
6
desplazamiento transversal - se pueden calcular inm: diatamente después
h A
de las influencias del desplazamiento M"ik.Designando el ángulo 3 E
h;,
con Djk,obtendremos
Los ángulos de giro en los extremos de las columnas se calcularáii
según la ecuación:
Calculados los ángulosde desplazamiento transversal Dikcon las influen-
cias de desplazamiento Mrrikobtendremos seguidamente la condición 11a.

47. Para un piso con coluninas de lo~igitudigual, serán iguales para todas las
colun~naslos valores D,, . En pisos con columilas de diferente loilgitud, serán
iguales todos los valores Dtk.hik.El cálciilo de los áiigulos de giro para nudos
nióviles se diferencia del cálculo de éstos, para el caso de los nudos fijos, úni-
camente en que en todos los extremos de las columiias se agrega el valor Di,.
Cuando se han obtenido los nionientos resultantes por otro procedi-
miento y debemos calcular los ángulos de desplazamiento transversal D,,,
a partir de ellos puede considerarse, en este caso, cada columiia i-k conio
una barra en cantilever empotrada elásticamente en su extremo superior k
y solicitada en su extremo libre inferior por la fuerza cortante Q,, y por el
momento resultante Mi,.
El ángulo de desplazamiento transversal Di, se compone, por lo tanto,
de cuatro valores:
T , debido al giro de la parte superior k del voladizo;
DO,, debido a la carga lateral exterior de la columna (si existe esta carga)
donde la columna se considera como una barra en cantilever:
Oik hik producida por la fuerza cortante Qs que actúa en la parte iii-
Kik ferior de la columna considerada como un voladizo;
3 Mi,- producida por el moniento flector Mi, que actúa eii la parte
2 Kik inferior de la columna supuesta como una viga en voladizo. Es
decir, la ecuación para la determinación del ángulo del despla-
zamiento transversal Di, de las columnas (cuaiido no conocemos
las influencias del desplazamiento M";,) será:
Debemos conocer en este caso los ángulos de giro T , de los extrenios
superiores de las columnas. Para ello debemos empezar calculando los
ángulos de giro T en las barras horizontales, mediante la misma ecuación
que hemos usado para nudos fijos, ya que las barras horizontales no sufren
ningún desplazamiento mutuo en sus extremos. Sigue luego el cálculo de
los,ángulos de desplazamiento transversal Di, (con la comprobación de la
condición 11a), y el cálculo de los ángulos de giro en los extremos de las
columnas. Comparando con el caso de estructuras con nudos fijos, debere-
mos agregar, además, el valor de Di,; Ti, se calculará entonces según la
siguiente fórmula:
IVZ~, 1 h Z k i
Ti, = Dik 4-TO;,+ -- --
2 Kik
(6 a)
Kik
El cálculo del ángulo de desplazamiento transversal D,, se empieza
siempre con el cálculo del giro T , de la parte superior de la columna. Es
absurdo y se puede omitir el cálculo de nuevo de estos ángulos de giro
en las cabezas de las columnas de valor Di,.

48. 46 P ~ K T I C O SDE V A R I O S PISOS
Ejemplo
Como ejemplo para la comprobación de un pórtico de vanos pisos
con nudos desplazables en dirección horizontal, sirve el esquema repre-
sentado en la figura 6. El cálculo de dicha' comprobación se ha efectuado
en la figura 9. Se ha supuesto que conocenios únicamente los momentos
resultantes. E1 cálculo de los ángulos de desplazamiento transversal Dik,
que es complicado, se explicará en el ejemplo.

49. CO.?IPROB.+CION DE L O S .110A11ES7 OS 1 0 1 . 1 I t . 5 17
FIemos anotado eii el esquema en los centros de las barras los valores
de las rigideces K de las barras y en los respectivos extremos de las barras
por encima de las vigas, o a la izquierda de las columnas los momentos
flectores definitivos. Además, en los centros de las columnas y por encima
de los valores de las rigideces K, hemos anotado el valor de Q h, es decir,
la suma de los momentos en los extremos de la colurnna respectiva con
signo opuesto.
Convprobación de la condición 1
En cada nudo, la suma de los momentos definitivos debe ser igual
a cero.
Comprobación de la condición 1n
En cada piso la suma de las fuerzas transversales de las columnas
debe ser igual a cero, ya que la estructura no tiene ninguna carga hori-
zontal. Debido a que, en nuestro caso, cada piso tiene coluninas de igual
longitud entre sí, debe ser la suma de los valores Q . h para cada uno de
ellos igual a cero. Por ejemplo, en el piso intermedio
- 1,02 - 1,83-0,87 $- 3,72 -O
Cuando las columnas de un piso no tienen la misma longitud, estos
valores deben multiplicarse por el factor de reducción c,* antes de hacer
la con~probación.
Comprobación de La condición 11
Como se ha explicado anteriormente, es necesario calcular primero
los áiigiilos de giro en los extremos de las barras horizontales (cuando
no sea posible el cálculo de los ángulos de desplazarniento transversal Di,
partiendo de las irifluencias del desplazamiento M",,). Deberemos calcular
los tres sumandos: ,wik 1 AtlkL
T - Tgik+ - - -
i k -
ICrk 2 Iíik
Cálculo de los sumandos de T,,: Para las barras 1-2, 4-5 y 8-9 con
una carga q = 1,8t/m (véase la fig. 3), tenemos
Para las otras barras horizontales, todas con la misma carga q =1,8 t/m
y además una carga concentrada Pz7.2 t en el tercio derecho, encontramos:

50. 18 P Ó R I I C O S DE I'AIi'1O.S P I S O S
Anotamos estos valores en el esquema en los extreriios correspoiidieii-
tes de las barras y por debajo de las misnias. .I,uego, mediante diclios -a-
. l J l k , ,
lores anotados, podemos determinar las relaciones - y - - , por
KLk 2 K,k
ejemplo, para la barra 2- 3
sumando los tres valores correspondientes encontramos los ángulos del
giro de la barra 2-3 iguales a +3,61 y -8,56 respectivanieilte. Cuando
hayamos eilcontrado los ángulos de giro para todos los extrenlos de las
barras horizontales, seguiremos con la comprobación de la condición 11a.
Para el cálculo de los ángulos debidos al desplazamiento transversal D,,
de los extremos de las columnas emplearemos la fórmula
En nuestro caso el término DO,k no debe considerarse, por no existir
ninguna carga horizontal en las columnas. El 1-alor de Ios ángulos B,,
lo hemos anotado en el esquema en la mitad de la columna y a la derecha
de su eje.
I{1 pririier térniiilo es el ingulo del giro Thdel extremo superior de la
columna, el cual se deduce de los ángulos de giro en los extremos de las
barras horizontales. Para la columna 5-2 el valor de Tk= + 3,6.
Para el cálculo del tercer término, segundo en nuestro caso, utiliza-
remos el valor de Q,, . Iz,, anotado junto a la columna. Para la colum-
na 5-2 este valor es -1,20, y dividido por K = 0,I da un valor de este
Q .hik -
-término - 12,O. Para el cálculo del tercer término de la co-
fii k 3 *lf,k
lumna 5-3e1 valor Jfik = + O,,52 y, por lo tanto, 7 = + 7,s.
'2 Kik
La suma de estos tres valores nos da el ángulo de desplazamiento
lateral del eje de la columna D, es decir, Dik= -O,6.
En pisos con coluniiias de la misma longitud deben ser iguales todos
los ángulos D, dentro de los límites de la posible exactitud. (En caso de
coluinilns tlesigiiales deben ser iguales los valores de Di, . h,, .)
I'ueden calcularse también los ángulos de giro en los extremos de las
coluninas:

51. ( O.lIPIIOIl.4 C I Ó S DI; [,O. 1IO.IICSTO.S 1 OTAL/; 49
El cálculo de los ángulos de giro en los extremos superiores de las co-
lumnas, debido a las causas anteriormente explicadas, no se efectúa. Los
valores TOikno deben considerarse, ya que no existe ninguna carga horizontal
en las columnas; es decir, se sumarán únicamente los tres términos. Para los
extremos inferiores de las columnas hemos anotado en el esquema los valores
correspondientes. El número inferior en dicho esquema es el valor del ángulo
de desplazamiento transversal de las columnas D, el cual para todas las
columnas del mismo piso tiene igual valor (cuando las columnas tienen la
misma longitud). Para la columna 5-2 vale -0,6. El número siguiente es el
Mi, 0,52valor -- es decir, para la columna 5-2: +-- = +5,2 y el tercer miembro:
Kik o,1
La suma de estos términos nos da el ángulo de giro en la parte inferior
de la columna, el cual debe coincidir con los ángulos de los extremos de las
barras horizontales en el mismo nudo.
Para poder comparar las diferencias obtenidas en los resultados del
cálculo de comprobación, vamos a hacer una coilsideración sobre concor-
dancias en los valores que podemos obtener. El cálculo de los momentos
definitivos con dos decimales representa, aproximadamente, un error
de 0,Ol. Al calcular los ángulos de giro en los extremos de las barras hori-
zontales se multiplican los momentos definitivos por números meilores
que 1. Por lo tanto, un error en 0,01 en el cálculo del momento resultante
da lugar a un error menor de 0,01 en el ángulo de giro. Al calcular los va-
lores de la deformación de las columnas en el piso superior se multiplican
los momentos resultantes por números iguales casi a 30. Por lo tanto, un
error de 0,01 en el momento resultante puede producir otro de hasta 0,3
en los ángulos de giro o en los de desplazamiento. Las comprobaciones
en la figura 9 quedan siempre en unos límites de exactitud que permiten
obtener los valores de los .momentos definitivos con una aproximación de
dos decimales.
A . Comprobación de los momentos definitivos en el caso de nudos fijo
Comprobación del equilibrio
Condición 1: En cada nudo i la suma de toda? los niomentos definitivos M;k
debe ser cero:
Z M i k = O
íi)
o cuando en el nudo actúa un momento exterior M i debe ser

52. 50 PORTICOS DE V A R I O S PISOS
Coitzprobación de las defovmaciones
Condición 11: En cada nudo i deben ser iguales los ángulos de giro de todas
las barras concurreiltes en el nudo y unidas a él rigidamente.
Designando con Toikel valor del ángulo de giro multiplicado por 3 E en el ex-
treiilo i, producido en la barra i-k libremente apoyada en ambos extremos y cargada
exterioriiiente, se obtiene este ángulo multiplicado por 3 E en el extremo i de la
barra i-k:
T . - y . Mik 1 .Wki
ik - ik + --- - - --
Kik 2 liiR
(6)
La suma de estos tres térininos para cada extremo de la barra se efectúa en el
esquema (fig. 9).
B. Coljzprobacz4n de los momentos definitivos en caso de nzcdos desplaznbles
Co>nprobacióndel equilibrio
Condición 1: Es la misma que en el caso de nudos fijos, es decir,
o cuando actúe en el nudo un momento exterior Mi
Z *TIik= Mi
(1)
Condición 1a: En cada piso Y la suma de las fuerzas cortantes en un plano
horizontal debe ser igual a la suma de las componentes horizontales de la carga que
actúa por encima del plano de corte Y :
r
Cuando la carga actúa directamente sobre las columnas (fuera de los nudos),
se determinan primero los puntos de inflexión en los diagramas de las fuerzas cortan-
tes para esta carga horizontal, suponiendo ambos extremos de la columna como
libremente apoyados. Efectuando los cortes horizontales por estos puntos de infle-
xión de las fuerzas cortantes (cuando la columna no está cargada directamente, el
lugar del corte horizontal es arbitrario) se obtendrá fácilniente la fuerza cortante para
cada columna con
Qik-- M,k + Mk,
hik
es decir, directamente de los valores de los momentos resultantes, lo cual permite
comprobar esta condición sin dificultad.
Comprobación de las deformaciones
Condición TI: En cada nudo i los ángulos de giro de todas las barras ngida-
mente unidas a él, deben ser iguales.
Debido al mutuo desplazamiento 6 de los extremos de las columnas, la recta de
6
unión de los extremos de la columna gira el ángulo -. %te ángulo, o el ángulo
h
de desplazamiento transversal Dik correspondiente multiplicado por 3 E, puede de-
terminarse más fácilmente partiendo de las influencias de desplazamiento Mf';k:

53. ('O.IIPRO».-ICI.ÓS »E LOS .IIO.IIE.YTO.S 1'01'.-lri'.s 51
E1 valor del ángiilo de qiro T,h (le1 extremo i :niiltiplicado por 3 1 en caso de
riiidos desplazables, se calculará con la fóriniila (esqiierria fig. 9):
T ,k es el valor del ángulo de giro inultiplicado por 3 L eil el extremo de la
barra 2-k libremente apoyada y cargada cori la carga exterior. (Este valor se encuen-
tra en los inaiiuales.)
Cuando iio coiiozcarnos las influencias del desplazamiento ?/I'',k deberemos
calcular los áilgulos de desplazaiiiiento transversal D,k partiendo de los momentos
definitivos en las barras. Cada coluninl i-k se considera como un trctrilo contilever
empotrado en el extremo k , y cargado además de la carga exterior en el extremo
!ibre i, por la fuerza cortante QZk y el iiiomento resultante Mik. Designando con Th
el valor del giro eii el estreino k iilultiplicado por 3 E y con Do;k al ángulo de giro
n~ultiplicadopor 3 B de la recta de unión de los extreinos de la colurrrna, que es la
viga en voladizo estáticanierite detenriinada bajo la carga exterior, obtendremos
Los ángulos de giro S,+deben por eilo determinarse antes del cálculo de los án-
gulos de desplazaniiento transversal Di,+.Como hemos detallado en la figura 9, debe-
rnos seguir en este caso el sigiiiente procedimiento:
1. Cálculo del ángulo Tik de giro de los extremos de las barras horizontales
(ya que éstos no giran por el desplazamiento transversal D;k, se efectúa el cálculo
como en el caso de una estructura con nudos fijos).
2. Cálculo del ángulo de desplazamiento transversal Dik según la ecuación (7 a).
3. Cálciilo de los restantes ángulos de giro Tikde los extremos de las c o l ~ ~ n a s .
(Cuando para el cálculo del ángulo de des lazamiento transversal Dik se utiliza el
angulo de giro T k en el empotramiento de & viga en voladizo, no es aconsejable re-
petir el cálculo de estos ángulos de giro Tk.)
Condición 11a: En cada piso Y debe ser igual el valor D i k .hik para todas las
columnas. Cuando todas las colunnas tienen la misma longitud, los ángulos de des-
plazarriiento transversal D;k so11 iguales para todas ellas.

54. V. ' Líneas de influenciaM
El cálculo de la línea de influencia de una estructura puede referirse
a la determinación de la elástica de dicha estructura bajo una carga deter-
minada, empleando el teorema de Maxwell, sobre la reciprocidad de las
FIG.10
0 es un ángulo arbitrario.
El signo de la línea de influencia
es contrario a la dirección de la inflexión 0 producida por el momento
flector M positisro en la sección considerada (véase fig. 10).
Para un ángulo 0 igual a 1, la elástica nos da directamente la línea
de influencia.
Para determinar la línea de influencia de una estructura para un mo-
mento flector actuando en el punto m, deberemos:
deformaciones.
Cuando provocamos, por ejemplo, en la viga continua dibujada en la
figura 10 una inflexión 0 en el punto m, la elástica correspondiente a esta
inflexión nos da la forma de la línea de influencia para un momento flec-
tor M en el punto m. Designando
m
9 por rj la ordenada de la elástica
a) iL 1 en un punto arbitrario, obtendre-
1. Producir en el punto m una inflexión 8,
I
: Y
2. Determinar los momentos correspondientes a esta deformación,
mos la ordenada q de la línea de
3. Dividir los momentos resultantes por B y dibujar las correspon-
dientes elásticas. Esta elástica es la línea de influencia que buscamos.
b) ,-- influencia con
Y$1 = -0
Es corriente la determinación de la línea de influencia como elástica
de la estr.uctura (n- 1) veces estáticamente indeterminada que se obtiene

55. suponieiido uiia articulacióii en el punto nl en el cual se produce la infle-
xión O. Para el cálculo de las distintas líiieas de influeiicia se coloca el
punto de articulacihn de tal foriiia que para cada líiiea de influencia exista
uii sisteina (iz -- 1) eces estáticamente i~idetermiriado.
X pesar de lo eiiuiiierado vanios a usar otro método basado eil las
siguientes ideas:
Efectuada la inflesióil 6, se da de nuevo a este punto uil estado de rigi-
dez (volviendo a soldarlo). Para la elástica esta soldadura iiu tieiie ninguna
influencia, pero explica el origeii de la línea de deforniacióii de otro modo,
ya que aliora el puiito de iiiflexión viielve a ser nuevamente rígido, 4- iio se
aprecian las propiedades elásticas de la viga deforniada por la inflesióil del
sistenia primitivo, Deberenios operar otra vez coi1 un sistema lz veces estáti-
camerite indeterininado. E1cálculo
se empezará supoiiieiido el estado
de eiiipotramieiito perfecto.
Eil este estado de enipo-
L A A. A
traniieilto perfecto 1)roducirernos
simultáiieamente, i o n la iiifle-
sión 6, eii el 1)iiiito nz unos mo-
mentos de fiiación en los extre-
Fra. 1 1
mos de este vallo, 10s cuales 110 permiten ningún giro de los extremos de
la barra (véase la fig. 11). Los otros tramos de la viga están descargados.
A1 áiigulo 6 se le puede dar uii valor arbitrario. Doblando el valor del
ángulo, quedan tanibién doblados los valores de las ordenadas de la elástica,
pero las ordenadas de la línea de iiifluericia rio varían al cambiar el ángulo 6.
1
Eligiendo, por ejemplo, el valor 6 = -- , y calculaildo para este valor los
2E
iiionientos de enipotrarniento perfecto eil los extrenlos del tranio eil que se
halla la seccihri 111, obteridrenios coi1 las notaciones indicadas en la figura 11:
Iinaginemos primero la barra cortada en ambos extremos y eil la sec-
ción m, las dos partes rectas a y b formando el ángulo 6. Luego se unen
estas partes rígidamente (por soldadura de las mismas). Dejemos luego
actuar libremente en los extremos de la barra los momentos M, y de tal
modo que hagan girar la viga otra vez a su situación primitiva (empotrada).
Además de estos dos momentos de fijación no intervienen en el estado
de empotramiento perfecto momentos de ninguna otra clase.
Anotados los dos momentos de empotramiento perfecto en los extre-
mos de la barra en el esquema de cálculo, calculamos los momentos defi-
nitivos del modo corriente.

56. Tamos ahora a demostrar cómo se obtiene de los iiiorneiitos resultan-
tes, la elástica y la línea de iilflueilcia correspoxidieilte.
Cuando una barra a - h (supuesta libre-
,, mente apoyada en anibos estreiiios) está car-
gada Úiiicameiite con el niomento flector en el
estreino Jfao se deforma, conio hemos dibujado
eii la figura 12, adoptarido una curva cuyas
ordenadas podenios calcular por la ecuación
y sustituyendo por el valor p. indepeiidieiite del inonieiito flector en el
extrenlo y de las dimeiisiones de la barra (pues sólo tlepeiideil de relaciones
relativas entre x, x' y 1)
1 x x' / + A '
= - - . - -3 / 1 1
ohtendrenios
?' =
.LIab ./
'P
2 EK
En el caso en que actúe en el extremo derecho el niomento Mb,, obten-
dremos los valores simétricos
1 x' x I 4- ,Y
P
3 1 1 1
Frc. 13
Las funciones p, y q~', como hemos dicho, son independientes de la luz
del tramo; sus valores se han llevado como ordenadas en la figura 13 en
cada uno de los diez puntos en que se ha dividido el tramo.

57. En el tratno correspoiidiente a la sección nz dcbetrios ademhs consi-
derar la influeiicia de la deforniacióil ocasionada poi la iiiflexióli O. Divi-
cliendo los mo~ilentosáefiiiitiros o las ordeliadac dc la elástica obtetiida.
1
con estos nionieiitos por el valor de O = ---, obtendrenios la línea de
2 E
iiifluencia, que se compone de las tres partes indicadas e11 figiira 11:
1. 1,a parte 77, producida por la infiexión O en la seccióii nz, sc elicueii-
tra únicamente en el tranio de dicha seccióil m.
1
2 La parte 7, -Mab. -. (1 producida por el niomento Al,!, .
K
L
3. 1,a parte =: ILI,, . -. g ' producida por el iiioincnto Al,,,
K
La línea de influencia para el momento flector eri la seccióii se
compone, en el tranio correspondiente a esta sección m, de tres térniiiios;
en todos los otros trailios, íinicamelite de dos términos, es decir, de 77, y 1 1 ~
En el caso de la líilea de influencia para el momento flector en el apoyo
de una barra, desaparece también en el tramo de la sección m la parte 7, y
entonces quedan así para todos los tramos únicamente los términos 7, y 7,
En este caso, los momentos de empotramiento perfecto, para la sec-
a b
ción m en el extremo izquierdo, es decir, para - = O y para - == 1, son:
1 1
Como ejemplo de cálculo de las líneas de influencia vamos a determinar
dos líneas de influencia para los momeiitos flectores de la viga continua
representada en la figura 15. Simultáneamente con este cálculo explicare-

58. 56 P Ó K T I C O . 5 D E V A R I O S P I S O S
mos el de las influencias del giro de los nudos en una viga continua, la cual
se puede considerar como un caso particular de uri pórtico de varios pisos.
No se estudiará aparte el cálculo de la viga continua ya que coinparándola
con uii pórtico de varios pisos rio presenta ninguna diferencia esencial.
El cálculo de las iiifluencias de los giros se ha explicado suficientemente
en los capítulos anteriores.
Ejemplo a
Calcularenios la línea de influencia para el momento flector en la
sección m de la viga continua representada en la figura 18.
1. Los momentos de er~ipotramientoperfecto, que úiiicamente apare-
cen en el tramo de la sección m, soii:
2. Determinación de las znfluencias del giro. Calcularenios primero
los factores de giro o coeficientes de repartición:
1 0,90
Apoyo 2. -- - . 1
= - 0.278;
O72 -
. ---
- - -- 0,222
2 0,90 -;0,72 2 0,9i) 1-0,72 -
Los momeiitos de enipotraniieiito perfecto y los factores de giro se
han anotado en el esquema de cálculo, figura 15(c. Luego se ha efectuado
el cálculo de las influeiicias de giro por el método explicado en las páginas
anteriores.

59. Los momentos definitivos en los extremos de las barras de la figura 15 a
los hemos anotado en la figura 15b por encima del eje de la viga. Por debajo
1 1
del mismo eje hemos anotado los correspondientesvalores Mik . - y M k ,.-
K K
por los cuales tenemos que multiplicar las funciones 9l y y' para obtener
los valores q, y q,.
1
Por ejemplo, eii el trarno 2, -- -- -0,018 -2- - 0,080.
100 -
K 0,90
Los valores de las futiciories p y y ' en cada una de las diez seccioiies
en que se ha subdividido el tranio se pueden tomar de la figura 13.
Momentos
Fxc. 15 b
1,a suma de los térniiiios q,, rl, y q, se puede hacer analítica o gráfi-
camente. Eii la figura 15 b se representa la líiiea de influencia definitiva
para el momento flector en la sección m. Se ha obtenido sumando gráfi-
camente los valores de las funciones g3y y' que se haii multiplicado por los
1 I
factores M,, - o Mki. - y los valores obtenidos q, y 7, se han dibu-
K K
jado en la mencionada figura.
Ejemplo b
1,ínea de influencia del momento flector en el apoyo izquierdo del ter-
cer tramo.
1. Mome?ztos de empotramiel.tto perfecto en los extremos de la barra
en el tercer tramo:
ill,b = -2 K = - 1,410
Mbo = -K = - 0,720

60. 2. Deternzilzación de las injltroncicts de giro (véase la fig. 16 a)
3. Los monz~niosdefiniiizlos se hall aiiotado en la figura 16 IJ por
encima del eje de la viga. Por debajo cle la rnisma se han anotado los fac-
1 1
tores correspoiidieiites 31,, y 1 , - para el cálculo de las tuncio-
K K
nes pl y y' (de la figura 13). 1,a suma de los términos 17, y 11, se ha llevado
a cabo del niismo modo que en el ejemplo a. El término 11, queda cupriinido
en este caso. La línea de influencia obtenida se ha dibujado en la figura 16 b.
Obtenida la línea de influencia para el momento flector M, en la
seccijn m, podenlos calcular el momento flector M, producido por cargas
uniforniemente repartidas en los tramos en que actúan con valores íinica-
meiite positivos o negativos.
Frc. 16 h
Designaremos con QiR, el área de la línea de influencia del nlomento M,
en el tramo i-k, con lo cual obtendremos el valor del momento flector 121,pro-
ducido por la carga q uniformemente repartida en dicho tramo con
M , = 4 . R',
El área Qu se puede obtener suniando las tres partes representadas
en la figura 14. El área de la función g. (es un número absoluto, sin dimen-
1
sión) tiene un valor de -y se obtendrá como valor del momento flec-
12
tor M, debido a la carga q uniformemente repartida en el tramo i-k.
a) Cuando el tramo i-k no corresponde al de la sección m
M,,, = -q' (mik -
12

61. I O) Cuando el tramo i-k corresponde al de la sección vi
eii la cual m,, y m,, son los factores del tramo i-k, que heilios obtenido
al calcular la línea de influencia M, (véaiise las figs. l.? O y 16 h) y sus
valores se obtienen en unidades de longitud (metros); a y b son las dis-
tancias de la sección m al apoyo izquierdo o dereclio respectiva~iiente,en
el tramo correspondiente.
Cuando hayamos calculado para cada tramo mediante los valores g, 1
y los factores m según a) o O), la parte correspondieiite del iiioineiito flec-
tor debido a este tramo, obtendremos el momento flector clefi~iitivoAIZ,,,
conlo suma de las influencias de todos los tramos.
En el cálculo de las líneas de influelicia para estructuras con nudos
desplazables, se obtiene la elástica que equivale a la línea de iiifluencia,
teniendo en cuenta también desplazamieiitos en el sentido perpeiidicular
al eje de flexión. El procedimiento explicado para determinar las líneas
de influencia debe ampliarse calculando la influencia del desplazamiento
(la cual no podemos dejar de tener en cuenta).
El desplazamiento transversal S, del extremo i de una barra con res-
pecto al extremo K se puede calcular por la fórmula que nos da la influen-
cia de dicho desplazainiento
MfCik. 1,k
aiR -
6 E . KIk
La línea de influencia se obtiene de la elástica correspondiente divi-
1
diendo esta última por 0 = --. El desplazamiento lateral S para un
2 E
traino de la línea de influencia es, por lo tanto,
(Véase la fig. 17)

62. La construcción de la línea de influencia, por ejemplo, la de la figu-
ra 17, se diferencia de la anteriormente obtenida tan sólo en que los
térniinos v,, 7 , y 7 , se suman a partir de la línea O - 1' -2' - 3' -4';
o sea, que las ordenadas de la nueva línea O -- 1' - 2' - 3' -4' quedan
desplazadas de la línea O - 1 - 2 -3 -4 en los valores 6,,-, 62,3,
Hasta ahora hemos hablado únicamente de la obtención de las líneas
de influencia para los rnomeiitos flectores.
Las líneas de influencia para las fuerzas cortantes, reacciones en los
apoyos, flechas elásticas, etc., se pueden obtener en la niisma forma, o
también calculando las líneas de influencia para los momentos en todos
los apoyos y eri todos los tramos correspondientes y de estos valores de-
ducir las líneas de influencia basándose en simples relaciones estáticas.
L a línea de znfluetzcia para el momento fleczov en u n a sección m se calcula en la
siguiente fornia:
1. Se calciilan en el tramo a-b de la sección m, los niomentos de enipotraiiiiento
1
perfecto producidos por la inflexión 8 = (véase la fig. 11):
2 E
y a continuación, en la forma conocida, las influencias del giro, las del desplazaiiiiento
(cuando existen) y los inoinentos definitivos.
1
2. Multiplicando los inon~entosdefinitivos por ei valor correspondiente de -
obtendremos los niultiplicadores para las funciones p y p' (véase la fig. 13).
3. Se dibujarán las líneas de influencia.
a ) No se suponen asientos en los apoyos de las vigas: partiendo ile un eje hori-
zontal se dibuja para el tramo de la sección tn el término 7, (fig. 14). Después se suinan
en todos los tramos a los valores anteriores los términos rl, y q3 Estos términos se
obtienen multiplicando las funciones p y q' por los respectivos factores (párr. 2).
La multiplicación resulta más sencilla efectuándola gráficamente.
b) Se suponen asientos en los apoyos d,e las vigas: los térniinos 1 5 , 11, y 7,
(figura 14) se dibujan como en la figura 17 partiendo de la línea O - 1' -2' - 3' - 4'
en lugar de hacerlo de la recta U - 1- 9 -3 -4. Los asientos (o desplazainientos
mutuos de los extremos de las barras en cada traiiío) se calcularán partiendo de las
influencias del desplazatniento Mf';k:
Mftik' l i k
aik= - --
3 Kik

63. VI. Estructuras c o n barras
de sección variable
El método descrito puede aplicarse también al caso de estructuras coi1
barras de sección variable. El desarrollo del cálculo es casi igual que para el
caso de barras con sección constante. 1,as propiedades elásticas de una barra
de sección vatiable pueden ser
definidas, conio es costumbre,
mediante los ángulos de giro:
a i k , a k i Y pik = p k i
indicados en la figura 18.
Puede demostrarse me-
diante la ley de Maxwell sobre
la reciprocidad de las deforma-
ciones que /lik = /lk,. Los án-
gulos u y /lpueden calcularse ~
gráfica o analíticamente por
los métodos elementales de la
-233-Estática, para cualquier varia-
ción del momento de inercia 1
a lo largo de la barra. Pueden FIG. lii
obtenerse también por medi-
ción directa en los extremos de las barras de modelos reducidos. Para los
tipos más corrientes de barras de estructuras se han confec~io~iadotablas
numéricas, de las cuales pueden ser obtenidos estos ánguloss. Debe obser-
varse, además, que según la regla de signos adoptada, se admiten como
@
1,as tablas con valores de los Angulos a y P, para los tipos de barras corrientes, simétri-
cas, así como los correspondientes términos de carga y momento? de empotramiento perfecto,
se encuentra, por ejemplo, en: uMétodo de los puntos fijos,),Dr. Ing. SUTER; <iEstriicti~ra~aporti-
cadas y vigas continuasl. Prof. Dr. Ing. GCLIJAK; u3Ianual para Ingenieros Civilesa. Profesor
Dr. Ing. SCHLRICHER.

64. positivos a partir del eje de la barra los ángulos de giro eii el sentido
de las agujas del reloj; por lo cual los ángulos /? son siempre negativos:
p i k = Bki < O
En las fórmulas se usa con preferencia el ángulo de giro positi~~o.
Definimos las siguientes relaciones numéricas que utilizarenios eii el
transcurso del cálciilo:
y, además, el coeficiente de barra derivado de estos valores
En el caso de barras con el momento de inercia constante es
a l k = a k i = 2 y a = ' !i13
El coeficiente de rigidez K, usado anteriormente, será, en el caso general
de barras de sección variable,
Esta fórmula está representada en forma que, en el caso especial de
barra con momento de inercia constante, nos dé el valor usado hasta ahora,
O sea, con
1
Ürk = ' 1 s Y (- p i k ) = - Jes, por lo tanto, K = -
6 E J I
Cuando los ángulos a i k , ski y Bik se obtienen mediante tablas, son
dados por regla general en la siguiente forma:
en las cuales se indican con t,, , tk, y tg los correspondientes de la tabla.
Luego:
1
y con ello el coeficiente de barra K de (VI-3) será
(VI-4)

65. En la figura 19 está indicado en fornia esquemática cómo se calculaii
los restantes ralores de los extreinos de barra y coeficiente de barra, así
coino el coeficiente de rigidez k, y los coeficientes t,, , t,, y tp, que han de
ser toinados de la tabla correspoil-
diente. Debe observarse que J , iio
tiene el niismo significado en todas = ol=+
las tablas. En general se indica con
J, el momento mínimo de inercia.
Para el cálculo del coeficiente de
rigidez K, según (VI- l), se emplea
siempre J , con el sigiiificado dado
en la tabla de valores, de la cual son FIG. 1:)
tomados los coeficientes t,, , tk, y t p .
En la figura 20 se indican los tres tipos de deforn~acióiique puede
experinientar la barra de una Estructura, y que aparecen cuando:
a) sólo gira el extremo i,
6) sólo gira el extremo k,1
c ) existe sólo un desplazanliento igual y contrario b de los extremos
de la barra.
En los gráficos de deforniacióii de la figttra 20 están indicados los
momentos extremos resultantes de las correspondientes deformaciones.
Por medio de la expresión siniplificada
se coiisigueii expresiones sencillas.

66. 6-i PÓRTIcOS B E V A R I O S PISOS
La exactitud de los valores anotados se puede deducir de manera senci-
lla cuando con los momentos extremos de la barra, indicados en la figura 20,
se calculan los ángulos de giro según fórmula (VI-5). Resulta de ella, en el
extremo i el ángwlo de giro t i , ,y en el extremo k,t k i = O . La figura 20 b puede
obtenerse de la 20 a por permutación de los índices i y k. La figura 20 c
puede obtenerse de las dos primeras, si se supone en este gráfico de defor-
mación que la barra se conserva vertical, ejecutando primero sus extremos
An giro de (- e),sin experimentar desviación. y luego otro giro en
cada extremo igual a: (Y
7ik = TkL = -
h,k
para los cuales se obtendrán los momeiltos estremos según a y b. ,4sí,
cuando la barra de una Estructura gira en sus extremos, los ángulos de
giro ti, y t k i , y experimenta además u11 desplazamiento transversal 5,
pueden obtenerse los momentos extremos correspondientes por suma de
los valores parciales de la figura 20. Por lo tanto:
1
-..-- ----
Designando nuevamente los momentos estremos de empotramiento
perfecto prbducidos por las cargas exteriores con M i k y M k i r y con
se obtiene la expresión general para el momento del extremo i de la ba-
rra ik con
aik + 1
Mik = -G,k+ nzrik",k + Mtk, + M f f i k- (XT1-8)
3
Obsérvese además que, según (VI-3)
pueden, por lo tanto, escribirse las expresiones (7) en la forma siguiente:
r
l
I
M'rk = 2 E K,k .7,k
,lI'k, = 2 E K,k .Tk,
1 (X-1-7a)
6 ~j M'',k = 6 E Krk. --
1 h k ,
La expresión de M",, no contiene ningún valor que dependa de un
extremo de la barra, o sea, que para cada barra sirve para arnbos extre-

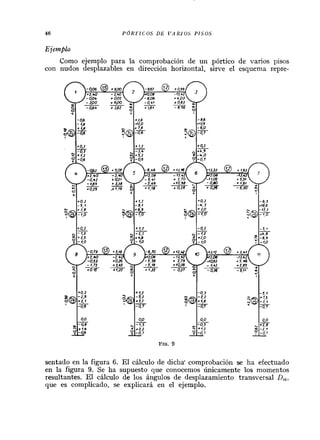
67. E S T R U C T U R A S C O N B.4 R R A S D E SECCIÓR' V A R I A OLE 6.i
mos; tenemos, por lo tanto, solamente una componente del desplaza-
miento M",lO. Si se designa además por:
se obtiene la expresión (8) para el momento extremo en la forma:
(VI-1O)
1 IM* = .U,>+ a. + +- M.,* bik 1 (VI-8 a)
Su diferencia respecto a la expresión correspondiente para barras con
sección constante, consiste tan sólo en que en aquel caso aik= 2 y bik= 1 .
La forma de calcular las componentes de giro M ' ; , , se obtiene ahora
de la condición de equilibrio del nudo i; es decir, de
Si se observa de nuevo que la suma de todos los momentos extremos
de empotramiento perfecto M;, de un nudo i es igual al momento de
fijación Mi, se puede escribir
Puesto que todos los extremos de las barras de un nudo i giran en
cada caso del mismo ángulo de giro t i , se obtiene, cuando para Mfikse in-
troduce el correspondiente valor de (7 a):
I W ' , ~
-- J(ik -
- -Pik
C iMfika,h C Tíik a,k
(i) íi)
Con lo cual sustituyendo ZMfika;, por la expresión anterior:
íii
--
11 M'. -- ~ i r[ M i + c i ~ * i+ c ~~~~k b;k] 1 (VI-I 1)
($1 1
en la cual se ha designado nuevamente como ,ui, el factor de giro:
(VI-12)
la En las ediciones 1 a la 4 de esta obra #Pórticos de varios pisos* se fij6 para M"ik
rl siguiente valor:
6 aik + 1h1"ih = 6 E Kik - ---
hik 3
L.:: 1,i cual para barras asimetricas existían dos valores diferentes para el desplazamiento.

68. Obtenidos los factores de giro, es conveniente efectuar eil cada nudo i
de la Estructura la comprobación de cálculo siguiente:
Si se trata de una Estructura con nudos no desplazables, con lo
cual M",, = O para todas las barras, se calculan las influencias de giro
según (11) en la niisnia fornia que para Estructuras con barras de seccióri
constante, con la sola diferencia de que los factores de giro han de calcularse
con la fórmula general (12). Posteriormente se desarrollará uil ejemplo
de cálculo para este caso.
Sabemos que para Estructuras de uno o varios pisos con columiias
verticales, no puede ser despreciado el desplazamiento lateral. El cálculo de
las influencias del desplazamiento de las columnas nos da lugar también, en
el caso general de barras con sección variable, a la condición de equilibrio:
la cual debe cumplirse en cada piso r. L a flíerza cortante del Piso se obten-
drá como antes de las fuerzas de fijación horizo~ztales,y las fuerzas cortan- ,
tes Qi, de las colurnnas, para esta condición de equilibrio, dependen tan
sólo de las componentes de los giros de los estretnos de las barras y despla-
zarnientos de las colurnnas. Resulta, pues,
y según (8a ) , multiplicando por una altura de columila h, arbitraria:
El factor de reducción c,, tendrá, en el caso general eli que estanlos
estudiando, la siguiente forma:
aik f 1Obsérvese aún que b,, = ; con lo cual se obtiene la condi-
ción de equilibrio con: 3

69. Debido a que, al desplazarse las coluniiias del piso Y todas experi-
nieiitan el iiiisiiio desplazainieilto trarisversal O, se obtieiie, cuaiido se
iritroduce para el valor correspondiente de (7 a ) :
, K i kj
-
-~
h i k-- - .- - . -- l'ik
<',ji . (.ki I c i k
1 ' - - - - jCik , L k i )
3 f.) Jlik
Si se iiitroduce, adeiiiás, la expresión (1-1), se obtiene conio procedi-
niieiito de cálciilo para la determinación de las componentes de despla-
zaiiiieiito con
l~ -~ ~ -. - - ..-
eii la cual , - - ~ ~y
es iiue-airietite el iiioiiieilto de piso. La fztevza cortante de piso Q, se calcztla
~c111ios?c?izaile todas las fuerzas H, aplicadas por encima del piso r:
1,os factores de corriniieiito (o coeficientes de tlesplazaiiiiento) vi,
tlt.1 piso Y se ohtieiieii, en el caso de columnas con nioniento de inercia
~-:~riat~le,coi^:
~- - ~ -
Tainbiéii, para los factores de corriniiento v, debemos insistir en la
c ~ i i eiiieiicia de efectuar una comprobación, antes de haber comenzado
t.1 cálculo de los valores de las componentes del nioniento. Calculados lo:;
:,ictores de corrirtiiento para la Estructura estudiada, debe efectuarse parz
:.I- coluninas de cada piso r la siguiente comprobación:

70. Puede observarse, por lo tanto, que para las Estructuras de pisos
con barras de sección variable, el cálculo de las influencias de giro A1f'lk
y de desplazamiento M",, es igual al principio que para las barras de
sección constante; sólo han de calcularse los valores auxiliares pík, v t k ,
btk y c , ~según las fórmulas expuestas. Los valores b,, y c,, no son iguales
para ambos extremos de una barra asimétrica, pero lo son eii el caso de
barras de sección constante, para las cuales
El cálculo de los momentos en los estremos de la barra a l~artirde las
influencias de los momentos, se obtiene con la fórmula (8a) de este cal~ítulo.
CÁLCULOD E LOS MOMENTOS D E EMPOTRAMlESTO PERFECTO
E N LOS EXTREMOS
Cuando se trata de una forma de barra y de carga que no existe
entre los valores tabulados, puede obtenerse en funcióri de los ángulos
de giro to,,tok, (fig. 21), producidos para
una carga determinada, cuando la barra
se supone libremeiite apoyada eil ambos
estremos.
De acuerdo con lo indicado en la fi-
gura 21, puede obtenerse el estado de em-
FIG.21
potramiento perfecto cuando se superpo-
nen las dos fases de las figuras 20 a y 20 b,
correspoildientes a unos ángulos de giro tIk= + , , y t k , = -+,, respec-
tivamente. Desaparecen entonces los ángulos de giro de los extremos de
las barras y quedan los siguientes monlentos de empotramiento perfecto
en los extremos:
-
T rk -- T C k i
M,k = -atk + -
P i k B l k
Mediante la fórmula (9) obtei~einosla expresión para el cálculo de los
momentos de empotramierito en los extremos.
Por razones de cálculo es siempre conveniente multiplicar por E los
ángulos de giro E ti,,E zOi, etc. Debemos observar que, siguiendo la regla

71. E S T R U C T U R A S C O N B A R R A S DE S E C C I ~ NV A R I A B L E 69
de signos establecida anteriormente, el ángulo de giro t k i , en el extremo
derecho de la barra ha de ser siempre negativo.
Para los casos de barras de uso más frecuente, con uno o con ambos
extremos acartelados, damos en el apéndice los coeficientes de barra a,,
y ski y el coeficiente de rigidez K,,. Se adjuntan, además, tablas para el
cálculo de los momentos de empotramiento en los extremos.
Para una barra simétrica, cargada en toda su longitud con una carga
uniforme q, puede ser obtenida la fórmula para el cálculo de los momen-
tos de empotramiento perfecto en los extremos. Con las notaciones usadas,
se obtiene en este caso:
1
Introduciendo este valor en la expresión (19) para la determinación
de los momentos de empotramiento perfecto en los extremos, se obtiene:
Para barras de sección constante a', = ski = 2 y entonces
Como se puede observar por las tablas del apéndice, tiene importan-
cia la existencia de acartelamientos aun relativamente pequeños, de ma-
iiera que el no tenerlos en cuenta en el cálculo afecta sensiblemente los
resultados.
El caso de barras articuladas en un extremo, que es corriente, por
ejemplo, en los tramos extremos de vigas continuas o en los pórticos con
columnas articuladas en su base, pueden ser consideradas de igual manera
(lue las barras restantes, sustituyendo la articulación por una barra ficticia
rígida a la flexión empotrada en su extremo (fig. 22). Esto da lugar, sin
eiribargo, a mayor número de nudos que el caso de que las barras articu-
ladas fueran perfectamente empotradas, o sea, que el cálculo es más la-
borioso.
Se puede, sin embargo, abreviar este cálcuio para el caso de barras con
sección variable, sustituyendo todas las barras articuladas por barras
ficticias. Se calculan primero los momentos de empotramiento perfecto en
. ' estrel~zos,para los apoyos realmente existentes, con los coeficientes reales

72. de las barras. Para las barras articuladas se calculan los momeritos de
empotramielito como vigas empotradas en un extremo al objeto de obte-
iier con ellos los monientos de fijación de los ilucios (fig. 23 a). EII las
tablas se dan. por lo general, sólo los valores de los monientos extremos
de empotraniiento perfecto para barras empotradas en ambos estre-
-
inos ( ~ ? i i , ~y EA,en fig. 23 b). De ellos se obtiene el moniento de enipotra-
~ilientoperfecto M,,de la viga empotrada sólo en un extremo (fig. 23 u)
-
cnandc: haciendo ,?a,, =; -ai,, se anula el nlo~ilentode empotramieilto
perfecto del extremo libre i por superposici6ii de la figura 33 u. Eii e!
otro extremo k queda después de esta superposicióii, coilio i~ioinento
extremo de enipotramieiito perfecto de la barra cuyo apoyo 2 puede
girar libremente (figura 23 o):
- - !l.¡l ,h
Llík"-Wtki --- - (1.1 '21)
([rk
Para vigas de sección coiistante con carga uniforinemente reparti-
da q, se obtiene, por ejemplo:
Si se calcula el momento extremo de erripotramierito perfecto Jí,,
a partir del ángulo de giro to,, de la barra libremente apoyada (fig. 21),
se obtieiie, debido a que sólo el estremo 1: está enipotrado:

73. '1:l't'It1.71:
-rey-!errcqelanb'"qoruar1xao~rraruo~nO~IL~IIIlaatrag'Qlesla&i<rrirl
o~ua!rrrszsldsappn%!sYior!2apoii-i%ri?~vnlS!eledlzri3el'orriar~saorrr.!rrr
lauasperlodrrrae!sjy~!jeneqz:rnrod'ouIallsaunriaepeliw!yiJ'y-!cllec;
e1szelduraa~as'sopnu301apU?!~EC!JapsoTuaruouIso1"isozlraLira.
ztaopaj~aaojua!utvyo&~taapso~ztatttoulsolvzw)tbsalau3sopv?ozt~
:dept?lS!!e
e2.1~3apose:,lazredsqqe.)se1uaanaqqoasa~uefauraselausuraa
u03(cz'%!j)orualTsaunua.c-.per~ocIrrray-!w.reqEIapolsaj
-rado~ua!rirer~oduraapornaqsaoTrraurorula'~2rer,apose3alcaered'arr
-ayc.loas(q1~)aCI.a~ua!puodsar~osopelnqe)ro1e.llasa':papuoa
:a~ua!n2rs~rrr~ojFIuaFYoi01!2ap
ojn2..ry;aselqelcqua'~elauaa01rod'epasOazl~,(o/!zlizW~LU~uittzVLV~
:euIrojc1rIa4orriaqsalarraolqsepe.i.)odrua
eucqE["p0~3ajradolrra!urer~odrrraaporuarlxao7uaworuIaauayqoas
"Yaop2uylealua~puodsar.so3opepqelroje.1la'y?u03expufasIenst.1rra
1
nosepassal
-en3se]ria'se31r?rrrnrrseIq-t.7se1ap?YwolnYugIap101e.2laeruolas1s

74. La barra ficticia empotrada en el extremo i puede ser elegida de sec-
ción constante (fig. 24 b).
En la figura 24 a se han indicado las deformaciones normales de la
barra real articulada; en la figura 24 b las de la barra ficticia. El coefi-
ciente de rigidez de la barra ficticia se ha indicado con K'; su longitud
a) Barra real b) Barra ficticia
Frc. 24
con h'. Si en la barra ficticia y en la barra real para la misnia deformación
han de ser iguales los monlentos extremos y viceversa, se tiene, para los
valores indicados en la figura 24:
La primera condición nos da:
y la segunda sustituyendo K' por el valor obtenido anteriormente nos da:

75. ESTh'Z'CTUR.4.5 C0.V RA R R A S D E SECCI6.V V.4 RI.4 RLE 73
Si se utilizan tablas numéricas para el cálculo de los coeficientes de
las barras, en las cuales se conoce el correspondiente ángulo en la forma
y en la cual se indica con f k , el valor tabulado correspondiente al ángulo a,i,
se obtiene el coeficiente de rigidez K' de la barra ficticia con
Si se ha calculado el coeficiente de rigidez K según la figura 19 para
la barra real, puede ser deducido de éste el coeficiente de rigidez de la
barra ficticia K'.
Si se sustituye a,, en (22) por a,, (- pik),
se obtiene, teniendo en cuenta la (3), el coe- [,Z t# b+
ficiente de rigidez de la barra ficticia con
K'= h.-!-
1 4fil
En esta expresión i se refiere al extremo de la barra con apoyo articu-
lado (fig. %5),en la cual a,, y Ü!h son los valores correspondientes a la barra
real. Puesto que a,, y a,i son diferentes para barras asimétricas debe obser-
varse que el valor ai,, de la expresión (22 b),se refiere al extremo con apoyo
articulado (compárese con fig. 19), por lo tanto, se ha de calcular con el
valor tkidel otro extremo. Para la barra ficticia alik= alki= 2 y bfik= $.
La barra ficticia es equivalente a la barra real por lo que respecta al
momento extremo M,, que proviene de t k i y 6, pero no sucede lo mismo
parala barra real según la figura 21 a:
y para la barra ficticia según la figura 2-1 b:
Introduciendo los valores de (22) y (23), resulta para la barra ficticia

76. Comparando el valor de la fuerza cortante obtenida para la barra
ficticia con la de la barra real en la expresión (N),se obtiene ei mismo
ángulo de giro t,,pero no el mismo desplazamiento 6. Pueden ser obtenidos,
sin embargo, los niismos valores si eil el caso de la barra ficticia se aiiade
3
un factor de corrección m = -- a la coniponente de la fuerza cortante
1
producida por el desplazamieiito transversal. En este caso debe comple-
mentarse la coiidición de equilibrio (1 l), obtenida para las frierzas ccrtaii-
tes de las columiias, introduciendo para las compoilentes de desplaza-
miento ,1ff;, el factor de correccióil m:
Por consideraciones análogas a las anteriores para la expresió11 (1 i),
se obtiene la fórmula para los factores de corrimiento con
Esta expresión sinle en general, es decir, aiin en los casos en que en
el piso hayan sólo algunas columnas ficticias o iio haya ninguna, si el íactor
de corrección m se establece coino sigiie y se usa la espresióii (18'):
3
El jactor de correcciów m tendrá zin valor m = -- para todns las barras
4
jicticias; es decir, para aquellas qiie szistif~iyena las colz~mnasarticilladas
E)% z b n extremo, mientras que para las colztinnas perjecta o elástica~neni~eun-
poiradas, tendrá el valor Irz = 1.
Cuando en un piso sólo existen algunas columnas articuladas, se iritro-
duceii para ellas, eii el cálculo de los factores de corriniiento v,, , los coefi-
3 hr .
cieiites correspondientes a las barras ficticias K', h', m = - y c',, = - ,
4 k'
mientras que para las restantes coliin~ilas,perfecta o parcialniente empo-
tradas, se han de ritilizar los coeficieiites realeh. K' = II, Iz' = h , nL = 1
J- los valores c,, y c,, segúii la espresión (13).
La coniprobacióii de cálculo para los factores de corriniieiito de 1111
piso, se obtiene^^ en este caso general de (18') con

77. Con los factores de corrimiento así obtenidos queda también invariable,
en este caso general, la expresióil (13) para las coinl~oi~entesde despla-
zainierito: --- - -- --- - -- --
-
N Af"lk = 1.$k [.Irr '-z.Ir Ctk - I l ' k , chal r.1-151
('1 ( 7 )
Piiesto que para la obtención de la fórniula de los factores de giro no
aparece la fuerza cortante, no soii ilecesarios, aun en el caso de las barras
ficticias, factores de corrección. La expresión (12) permanece invariable.
Para las columnas con apoyos articulados se iiltroducen los coefi-
cientes de las columnas ficticias K' y a' = '2; para las otras harras, los
valores reales.
T,a comprobación de cálculo para los factores de giro segíin (12') per-
manece iilvariable, aun en el caso de que en el nudo concurran alguiias
harras ficticias sustituyendo a las harras articuladas en uti extremo:
Se designa con a',, el valor correspondiente a ai, que debe ponerse
eti cada caso; es decir, ali, = 2, para la barra ficticia que sustitiiye a la
barra articulada en un extremo; para las otras barras el valor real a,k.
Calculadas las componentes de giro y de desplazamiento definitivos,
se obtienen los correspondiei~tesmomeiltos extremos mediante (8 a):
Tainbiéil los momentos extremos de las harras articuladas han de
calcularse con los correspondientes valores de las barras ficticias: a',, = 2
y O',, = 1. O sea, todas las operacioiles de cálculo deben liacerse con los
valores de las barras ficticias, con excepción del cálczrlo de los monzentos
E I I I ~ ~ P ~ Z O Sde etnfiotramiento perfecto [los cuales se calculail mediante una
tlc las expresiones (21)] y de las fzlerzas de fijación horizontal.
Para el caso de una Estriictura simétrica con carga simétrica es sufi-
ciente, autl en el caso de barras de sección ~rariable,efectuar el cálciilo

78. '76 Q d R T I C O S »E V A R I O S P I S O S
sólo para la mitad de la Estructura; a este fiil cada barra cortada por el
eje de simetría es reemplazada por una barra ficticia empotrada, con un
coeficiente de rigidez
En la cual K y a = a,, = a,, son los coeficientes reales de la barra.
Mediante tablas en las cuales se dan los valores de los ángulos de giro
de las barras con
1 1
a,k = a), tLk - - y - PLk- t p --
E lo E l o
y donde ti, y t son los coeficieiltes tabulados. puede ser también calculado
el coeficiente de rigidez K" de la barra ficticia con
Esta fórmula se obtiene introduciendo el ~ a l o rK" de (4) en la expre-
sión anterior y se observa, además, que para barras simétricas
Para cargas antimétricas considerarerilos uii punto de iilflexióil en
la iriitad de la barra, eií el cual queda cortada por el eje de simetría, y se
comporta como si hubiese una articulacihri eil este punto. Se supone, por
lo tanto, como barra ficticia la niitad de la misma con una articulación
en el eje de simetría. Debido a ello deben emplearse en el caso de carga
antimttrica, factores de giro distintos que 1)ara carga simétrica.
El coeficierite de rigidez de la barra ficticia se obtiene, para el caso
de Estructura simétrica y carga antimétrica de manera parecida coi1
Debemos znsistir rrna vez más, qzte las barras ficticias se introditcev~
en el cálcrdo despzlés de determinados los momentos extrentos de enzpotvu-
miento perfecto y sólo a fin de poder calcular los momentos extrevzos más
jácilvzente. Los coeficiet~tesde las barras ficticias (K', h' y a -2) aparecen
en el cdlczrlo inmediataitlente después de la determinación de los nzonzentos
extrenzos de empotramiento perfecto y tan sólo hasta que se hayan obtenido
los nzovzentos finales. Despz~ésde esto, dehe prescindirse de las barras ficticias.

79. ESTRUCTURAS CON B.4RR.4S DE S E C C I ~ Nl.'ARIA BLE 77
Ejemplo 1
Cálculo de los momentos totales de la Estructura de varios pisos indi-
cada en la figura 26 a bajo ia acción del viento q, = 0,5 t/m. Los valores
iiecesarios están anotados en cada barra. El cálculo de los coeficientes de
rigidez K ha sido hecho en la figura 26 b de acuerdo con los valores de la
iiq~ira19, y para las columnas con base articulada, con los de la figura 28.

80. 7 8 PÓRTICíl. D E V.4 RIOS PISOS
Los momentos de empotramiento perfecto en los extremos se calculan
antes de introducir las barras ficticias, o sea, con los coeficientes reales de
las barras. Para las columnas de la izquierda (cargadas) de los dos pisos
superiores, que so11de sección constante:
La columna 8-12 es de seccicín variable y está articulada en el apo-
yo 12.,La articulación de este apoyo de la columna debe transformarse en
empotramiento perfecto. El momento de empotramiento perfecto en el
extremo 8 se calcula mediante alguna de las fórmulas (21) o 21 a hasta e.
Si suponenios que sólo se dispone de tablas auxiliares para ángulos de giro,
que proporcionan estos ángulos para una carga unifornie q, en la forma:
J
Para la longitud de acartelamiento A = 0,30 1 y -" = 0,200 (véase
figura 26 b), se obtiene el coeficiente tabulado . I s
E1 coeficieiite t,,,,, para el ángiilo de giro as,,- se tonia también de
tablas y se anota eii la figura 26 b para el extremo 8,lL coi1 t3,1z= 0,207.
Así, pues, según (21c):
Las fzrerzas de fijaciu'tz covrespondientes al empotramiento perfecto se ob-
tieneii como reacciones en los apoyos ficticios y son las que en la horizontal
de la viga del piso inipideii el desplazai~iientode éste. Para las vigas 1,
I I , I I I , se obtierieii las siguieiites fuerzas de fijación:
Debido a la asimetría de la columna 8-12, aun en estado de empotra-
miento perfecto de ambos extremos, la carga exterior no produce iguales
reacciones de apoyo, siendo:

81. E S T R l ' ( ' i (.li.-1.5 ('0.Y If.4RRA.S D E S E C C I Ó S IJ.4 XI.4 B L E 79
Toiilaiiclo para valor de la altura de piso h, para hl = 3,50 m,
hll = 2,00ni, y en el piso inferior igual a la longitud de las columiias
ficticias con
/ l I l 1 = a/2 /1 = 3 1 2 6,00 = 9,O 111
se obtieiieii los siguientes ?~zottle~~tosde piso.
.%iiotados en el esquema de cálculo los niomentos de piso, los mo-
nientos extrenios de enipotraniiento perfecto y los monientos de fijación
de los nudos deducidos de los anteriores (fig. 28), se procede al cálculo de
los factores de giro y desplazamiento, para lo cual se reemplazan las barras
articuladas por barras ficticias que las sustituyan. Para mayor claridad,
se ha hecho el cálculo de los factores de giro y desplazamiento separadar
~iienteen la figura 27.
Para el cálculo de los /actores de giro según (12) y (12') son necesarios,
para barras de sección variable, además de los coeficientes de rigidez K
los coeficientes a,, y ak,. Para estas barras, destacadas en la figura 27
coi1 trazo niás fuerte, se hari anotado los coeficientes aaken los correspon-
dientes extrenios. Para las barras que tienen coeficientes correspondientes
a sección constante, y, por lo tanto, tanibiéil para las barras ficticias,
atk = a,, = 2. Los factores de giro se han calculado según la fórmula (12'),
que se ha escrito también en la figura 27. Así, por ejemplo, para el iiudo 9:
y con ello segúii (12'):
I,a comprobación de cálculo segúii (12' a) es:

82. Los factores de corrimiento o coeficientes de desplazamiento se han
calculado según (18) o (18'). En primer lugar se calculan los coeficientes
de barra bik y cik de los valores aik, según las expresiones (10) y (13), las
cuales se han escrito también en la parte superior derecha de la figura 27.

83. E S T R U C T G R A S CO"l B A R R A S D E S E C C I Ó N V A R I A B L E
En pisos con columnas de diferentes alturas es necesario, además, el valor
h
específico de barra 2,y cuando hay columnas con apoyos articulados,
hik
también los factores de corrección m. Este caso, el más general de todos,

84. se prese~itaeri el iíltiriio piso, en el ciial se liaii anotado estos -alores e11el
celitro de las colu~iilias,figura 27. Para coliiiniias de sección constante
b,, -1, y cuando todas las coluninas del piso son de igual longitud, el
Iiy 1. No es necesario, por lo t;i~ito,la anotaciói~de los-alor de h, es -- =
h t k
valorcs b,, y c,, . Después de anotados estos valores en la figura 27, sigue
el cálculo de los factores de desplazainiento según la fórrri~ila(18'), la cual
ta1iibii.n se ha escrito en la figura 27. Se obtiene así, por ejeixiplo, cn el
piso inferior, para el cual se ha elegido el valor lz, igual a 9,O m:
Que puetleri coriiprobarse con (18 a):
El i~ílcztlode los tno?ne+ztosdebidos al giro M',, y JI",, ha sido hecho
eii la figura 28. Aiiotados en el esquema los monieiltos de piso, los niomen-
tos extremos de enipotramiento perfecto, los morrientos de fijación obte-
nidos de los anteriores, los factores de giro y los factores de desplazamiento,
sigue el cálculo de los i~iomentosdebidos al giro según expresiones (11)
y ( l ñ ) , los cuales se hall anotado, nuevamente, en la parte baja y a la de-
recha de la figura 28. Como se deduce de estas expresiones, son necesarios
tani1)iéii los ralores b,, y c,, para las barras de seccióii variable. Teniendo
en cuenta que a1 efectuar las sumas debeii multiplicarse, en cada caso,
los M',, por los correspondientes valores c , ~ , y los ill",, por los b,, , es coii-
-eiiieiite aiiotar los valores c,, en los extremos de las barras y los valores b,,
juiitos a los Llf",,(véase fig. 28).
Se eiiipieza el cálculo con la piiniera iteración para la obtención
de las iiifluencias de desplazamiento, pues éstas nos darán, para el caso de
carga horizoiital, el valor más importante de los momentos extremos. Para
ello se suponen, eii priiicipio, iguales a cero todos los M',,, si no disponen~os
de mejores valores aproximados. Debido a las coiiiprobaciones autoniá-
ticas que presenta este niétodo de cálculo, los valores iniciales no tienen
iiinguila influencia eii los resultados finales, sino tan sólo en la rapidez
de con-ergerici:~.Por eleccióii iriadeciiada de los valores iniciales puede
llegar a ser necesario, a lo sunio, un gran número de iteraciones. Teniendo
eri cuenta cjue en la figura 8 se ha calculado una Estructura para la misnia

85. carga, pueden utilizarse las influencias obtenidas allí. Estos valores son,
por lo tanto, anotados en la figura 28 como una primera aproxiniacióii
de las influencias de giro.
En el piso no existen columnas de seccióii variable, por lo ciial, por
ser b,, = 1 para todas las coluninas, no hay niiigiina diferencia en el cálcillc
de las iiifluencias de desplazamiento ilf",, comparado con el cálciilo de
Estructuras con barras de sección constante. En el caso de columnas con
sección variable, la diferencia consiste solaniente en que al sumar las in-
fluencias M',, se ha de tiiultiplicar cada una de ellas por el valor c,, corres-
pondiente a este estrenio. El cálculo de las influencias sigl~ede igual manera
en todas las iteraciones sucesivas. Como ejemplo de la niarcha seguida, es
suficiente detallar el cálculo de una iteración. En la figura 28 se han llevado',
a cabo tres iteraciones sucesivas de las influeiicias del desplazamiento.
Como comprobación se ha realizado otra iteración para el último pix.
3Iultiplicando esta sunia por los factores de desplazaiiiiento de este
piso, se obtienen las influencias de desplazamiento de las cuatro columnas
con valores:
-- 1,25 - 3 - 6,81 - - 6,81
Obteniéndose los mismos valores que en la iteración anterior. Los
valores definitivos han sido, pues, conseguidos en la tercera iteración.
De igual forma se obtiene para el piso interniedio:
AIultiplicando esta suma por los corres~>ondientesfactores de desplax
niiento, se obtienen las influencias de des~~lazaniieiitode este pise:
El cálclrlo de Ins i~zflzrenctusde giro, cuando hay barras de sección
variable, se diferencia del cálculo para Estructuras con barras de sec-
ción *constantetan sólo en que, al efectuar la suma, se hall de multiplicar las
influencias del desplazamiento en cada caso por los correspondientes fac-
tores b,, . Debe observarse de nuevo, que, aunque es completame~itearbi-
trario el orden seguido de un nudo a otro, puede, sin enlbargo, iiifliur
tiotablemente en la rhpida coilr-ergeiicia. Es conveniente empezar por los
nudos en los cuales so11 de esperar mayores cairibios respecto a las influen-
cias de giro coi1 respecto a la etapa anterior. Se debe empezar, por lo tanto,
por los nudos (iniás desequilibrados)). En iiiiestro caso el orden más con-
-eilieiite es el siguiente: 8, 11, 10, 9 y liiego 1: 7, ti, 3, etc.
Puesto (lile para todas las barras del ~iudo8, 0,, = 1,0, es exactamente
!» misnio que para e1 caso de Estructuras con barras de seccióii constante:

86. 83 P ~ R T I c O SD E V A R I O S PISOS
Con la multiplicación por los correspondientes factores de giro -0,052,
-0,386 y -0,062, se obtienen las respectivas influeiicias de giro
prácticamente los mismos valores de la iteración anterior.
Para el nudo 11, por ejemplo:
Por multiplicación de los correspondientes factores de giro se obtie-
nen las influencias de giro de este nudo
Cuando todos los nudos han sido recorridos, de modo que tanto para
las influencias de.giro como para las componentes de desplazamiento
no resultan diferencias esenciales respecto a la iteración anterior, pueden
ser consideradas como definitivas las influencias de momento obtenidas.
Los momentos extremos se obtienen de las iilfluencias de momento
mediante la fórmula (8a):
En el caso de barras de sección variable, existe sólo la diferencia de
que en lugar de los valores fijos a,, = 2 y b,, = 1 se obtienen otros valores ,
para a,, y bsk según la forma de la barra.
El cálculo de los momentos extremos puede ser efectuado en el misnio
esquema de cálculo en el cual han sido calculadas las influencias de los
momentos (fig. 28). En el presente ejemplo se ha hecho este cálculo por
separado para mayor claridad, en la figura 29.
Trasladados al nuevo esquema los momentos extremos de enipotra-
miento perfecto, las influencias de giro y las de desplazamiento, se anotaii
los valores a,, y bZk en las barras de sección variable (las ciiales se ha11
destacado en la figura con trazo más fuerte).
Efectuada la multiplicación por los valores a,, y b,, , de acuerdo a
(8 a), se han anotado las influencias una debajo de otra, para obtener por
sunia de las misrras los momentos extremos. Así, por ejemplo, para los
extremos de barra 6, 10 y 10, 14:

87. uossepesguaillasrrapandseJs?anbeñ'ouq!lmbaapsauo!seqoldwosse1
'souawopuens'ienjsaga'sowa~~xasoJuawowsolapsaloleilsolelede~ald
-wosuo!s.eqoldruoseunoq~s.eeilallasouopuens'alqepuawosalSS
.qge1&!3eluasopeJpsalsolu.eJoueasñaJuawlo!laJu.e.e~ps
-cap(ailalqsyw)~mo3eluaolnsl?slaop!n8aseyas(s-e!s!~s!js.e~~.eqse1
.el.edu?!qrueJ'OJUEJ01lodñ)aJueJsuosupsasaps-elleqse1.el.ed

88. mil- POCG trabajo. Debida R que en el presente ejeniplo iio zctúan iiioiiieil-
tos exteriores el; niriguno de los nudos, la sunia de los iii~i~ieiito~extrenlo5
debe ser igual a celo en cada nudo:
Para los i~ioniei~tosextreinos de la figura 12 se ha ciiiirplido esta coiii-
probaciói~con suficiente exactitud para todos los nudos.
Otras co;iiprobaciones de equilibrio se obtieileii llar consideracitjli
dcl equilibrio de los distintos pisos, con 10 cual se obteiidrán tantas con-
diciones de corripro:)asióil conio pisos existan.
Así la suma de las fuerzas horizontales para una seccióii por el ,piso
superior de la figura 29, por ejemplo, a la altura de los extreinos inferiores
de las columiias, nos da:
Fuerzas exteriores:
0,st!iil .3,50 iii = 1.7,5 t
Fuerzas cortantes de las columnas:
Para una sección por el piso intermedio, a la altura de los estreriios
inferiores de las columnas, se obtiene:
Fuerzas exteriores:
0,s tlni . (3,50- 4,OO) iii - 3.75 t
Fuerzas cortantes de las columnas:
1,73 + 0,73
-- 3,7,5 tt - - -
4,0
Para el piso inferior:
Fuerzas exteriores:
0,s t/tri (3,50 4.0 6.0)111 - R,75 t
Fuerzas cortantes de las colun~nas:

89. Ejemplo 2
Cálculo de la línea de influeiicia para el nloinerito fledor en la sec-
ción 7n de la figura 30. Esta figura 30 tieiie las misnias luces de la 15, pero
esta últinia tiene vigas coi1 ricartelamie~itos.
14a viga tieiie en el centro de la barra u11 momento de inercia J o = 3,6
y eii las secciones 3 y 4 un J,,, = 16,3fi.
CáEcirlo de los coeiiciefttes de rigidez de las barras
1311 el tranio con momento de inercia constante:
3 1 0 7 5 . 3 6
barra 0 - 1 1 ' = - - = - - - = 7,s
4 L 3.60
Para las barras con acartelaniieiitos pueden ser tomados los coeficientes
de rigidez de las tablas 1y 11a , págiiias 92 y 0.3.11
Por interpolación se obtienen los siguientes valores:
~ ~
! 71 i J,a, ~ I
Iiarra 1. == - - J o
nk, i fCik c -
Ií'
a i k i1 JO ; N 1 barras ficticias ;
l1 Para ~ t r a sfuriiias de barras pueden ser usadas las t a l h i indicadas en la llamada 9, ~ 1 1
las cuales se dan lri.; ángulos de giro eri la siguictite forma,
,.,. - t . 1 1 1
ik - r k ; Ciki y- y (- Dhi) =
fi Jo t.J o P J ,
ciialldo ha11sido iiiilicados con l i k , tki, tb, los correspr~lidientesvalores tabiilados. Con estos valores
se obtienen:
'kz !ik ñ,k " 1a i k =~-; a k , = -
t~ t~ ü ; k ' ¿ikL- 1
Resultari<iolos coeficientes dc rigidez K según (2)

90. 88 PORTICOS DE V.4RIOS PISOS
El coeficiente de rigidez K', de la barra ficticia, ha sido calculado con la
fórmula de K dada anteriormente, es decir, según las expresiones (22b) y (2).
Valores conslanles de la barra
Valores
Valores ". . - - . .
(( 0 para la barra
Los momentos extremos de em;botramiento ;berfecto producidos por un
1
ángulo 8 = -en el tramo m (véase pág. 53), existen sólo en el tramo
2 E
de la sección m y valen
7
1
1
En el ejemplo presente son:
CbLcuLo de Los factores de giro
K,k,<ik =
2 aik Kik
Apoyo 1:
Apoyo 2:
- 0,90 - 1,O2
Fa,, = = -0,267, p = -0,303
2,O. 0,90 + 1,54 2,O . 0,90 + 1,54 . 1,Oil
Apoyo 3:
- 1,02 - 0,94
l 4 , a = - = -0,281; ps,4= - = -0,259
2,082 1,02+ 1,605.0,94 2,082 . 1,02 -1- 1,605.0,94
Apoyo 4:
-0,94 -0,652
= -0,334; p,,, =
-
¡*4,3 = - -0,232
1,605 0,94+2,0 .0,652 1,605. 0.94 +2,O. 0,652

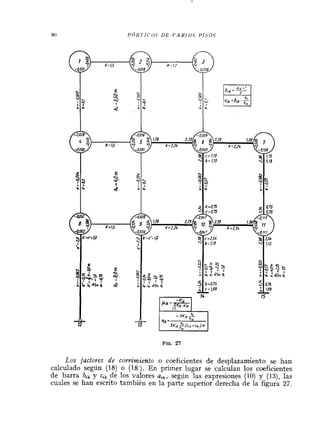
91. ESTRUCTUR.4S CON B A R R A S DE SECCIOiV V A R I A B L E 89
Como comprobación de los factores de giro se utiliza Z ajk . ,uik= -. 1.
(i)
Los momentos de empotramiento perfecto, los factores de giro y los valo-
res a están anotados en el esquema de cálculo (fig. 31). El cálculo de las
influencias de giro se prosigue de la manera corriente, es decir, como en
el caso de vigas con momento de inercia constante. Los momentos extre-
mos de la barra se obtienen de la siguiente expresión:
El cálculo de los momentos extremos de la barra puede verse en la figura31.
De estos momentos extremos se obtiene la línea de influencia, de la
misma manera que en el caso de vigas con monientos de inercia constante;
es decir, por suma de los tres términos r],, r], y 7, (véase fig. 14). La compo-
nente ql, que sólo existe en el tramo de la sección m , tiene la forma indicada
en la figura 14a, mientras las componentes 7, y q, pueden ser obtenidas
de la misma forma como anteriormente;
es decir, con M~~-r
f l
Representemos de nuevo por
l2 i2
- P Y -v'
J s J o i
las flexiones de un piinto cualquiera del
tramo i-k multiplicadas por 2 E , cuando
* k
en el extremo i o k se aplica un momento FIQ.32
extremo Mi, = 1 ó M,, = 1, respectiva-
mente.
De la figura 32 se deduce que en lugar de la línea de deformación
de un rriomento extremo Mi,, pueden ser sustituidos los valores corres-
pondientes a la línea de influencia del ángulo extremo de giro del tramo
libremente apoyado i-k, por valores que figuran en tablas auxiliares.

92. Mediante tablas para las líneas de itlflueiicia de los áilgtilos estretilos
de giro, que tienen la forma
en las cuales t, y tk son los correspondietltes valores tabulados, se ohtietieii
las fuilciones (I y y' con
(P = 2 t , y q'= 2 f k
Por consiguiente, los números tabulados de la línea de itlfliieticia, da11
para los ángulos extremos de giro, del tramo supuesto libremeiite apoyado,
la mitad del valor de las funciones p, y p'.
Funciones Q y Q' de los t r m s cm cartdas
En la figura 33 se dan los valores de las funciones y y cpr, determitia-
das de este modo para los tramos 2-3, 3-4 y 4-5.12
En la figura 34 se han anotado en primer lugar los momentos extre-
mos determinados en la figura 31, debajo de los correspondientes factores
l2
de corrección Mik - -, por los cuales han de ser multiplicadas las furi-
.To
ciones rp y y' para obtener los términos 7, y 7, de la línea de influencia.
Por suma de los términos qi,q2 y qg ha sido obtenida en la figura 34 b la
línea de influencia para el momento de flexión en la sección del tramo 3-4,
de igual forma que en la figura 15 b.
Una comparación de la línea de influencia de la figura 34 con la le la
figura 13 b muestra que, al suprimir las cartelas, las ordenadas de la Iinea
de influencia de la sección m aumentan alrededor del 15 %.
Puesto que las barras ficticias son introducidas sólo para conseguir
una mayor rapidez en la determinación de los momentos extremos, se com-
prueba, para el cálculo de las componentes 7, utilizando los valores de las
barras realmente existentes.
l2 Estos valores numéricos han sido obtenidos por interpelación de las tablas auxiliares
del Prof. GULDAN,<<Estructurasporticada5 y vigas continuasi), segunda edición, paginas 342 y 349.

93. Eii general será necesario calcular la línea de influencia en cada tra-
nio para arias secciones. Es coilvenieiite entonces c:ilciilar, de la manera
explicada, las líneas de irifluei~ciade los rrioi~ientosde flexióii sólo eii las
seccioiies de los apoyos. Para otra sección cualcluiera del tramo puede
obtenerse la línea de influencia para el momento de flexión, la fuerza cor-
tante etc., de la manera conocida, de las líneas cle influeiicia de los nio-
ineiitos (le1 referido tranio por suma de loa tres térniirios.
El cálculo de la línea de influencia para el inomerito de flesión en el
apoyo, se diferencia del cálculo indicado aiiteriornieiite para la línea de
influencia del momeiito de flexión de la sección m, solametite eii que el
a) Momentos m
Frc. 34
término 77, desaparece; de manera que la línea de influencia se obtiene
para todos los apoyos como suma de dos componentes; es decir, 11, y q,.
E n el presente ejemplo se ha indicado esto, en la barra 1-5, para la
sección 1, en el extremo izquierdo de la barra.
1,os niomentos extremos de exnpotraniiento perfecto son, en este caso,
(z b
con - =. 0 y -- = 1:
1 z
Si se considera que en los extremos de las barras libreniente apoyadas
no pueden aparecer momentos de empotranliento, el tnon~eiitode em-
lmtrainiento perfecto en el extremo izquierdo, para la barra empotrada en
un extremo, es:
Luego se sigue el cálculo de niaiiera análoga a la explicada anterior-
niente.

94. TARLA1. Vigas sim4tricas con cartelas
Número superior aik= ski
'-
Número inferior c
J o
Para el coeficiente de rigidez Kik= c - -1
,Q
Monientos extremos de empotramiento perfecto:

95. TABLA11 a. Vigas con cartela en un extremo
Número superior ai,
Número intermedio ahi
Número inferior c
JoPara el coeficiente de rigidez K,, = c . -
1
I I l
Entre A - = 1 y A = 0,25 no se debe interpolar

96. T x n r , ~IIh. Momentos extremos de empotramiento perfecto en vigas con cartela
en un extremo para carga uriilormemente repartida
-
JILk= - c1 q 12, c1 = número superior
k
-
Mk!= - c2 q 12, c2 = níiniero inferior
Tabla de los valores c, y c,
t e ? = 1 y A = 0,'Lt7 no se debe interpolar

97. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Definiciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11. Estructuras con nudos rígidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Casos particulares
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Kesuiiieri del capitulo 11
. . . . . .I I I. Pórtico de varios pisos con nudos desplazables en sentido horizontal
Tiifliiciicia ilel desplazaiiiiento de los riiidos . . . . . . . . . . . . . . . . . . . . . . . . . . .
Carxas verticales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Coliiiiinas articiiladas en los apoyos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Cargas horizont:iles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Coliiinnas de tlifrreiite altura en iiii iiiisiiio piso . . . . . . . . . . . . . . . . . . . . .
Coliimnas articuladas en los apoyos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Resiiiiien clel capítiilo 111 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
IV. Comprobación automatica de los momentos totales . . . . . . . . . . . . . . . . . . . . .
1. Estructiiras coii niidos rígidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
E Pórtico de varios pisos con nuilos desplazables en sentidu horizontal .
Resuriien del capítulo IV . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
V. Líneas de influencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
I'striicturas con iiutlos fijos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Caso de carga iiiiifonnemente repartida . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .d
Estriicturas con nudos desplazables
Kesiiiiien del capitulo V . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
VI. Estructuras con barras de sección variable . . . . . . . . . . . . . . . . . . . . . . . . . . .
Cá:ciilo de los momentos de empotraniiento perfecto en los extreiiios . . . .
Barras articuladas en los apoyos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
L:,structuras siniétricas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
..I . i n r . ~1. Vigas siniétricas con cartelas . . . . . . . . . . . . . . . . . . . . . . . . . . .
T . 4 1 3 ~ ~11ii . Ilgas con cartela en un extremo . . . . . . . . . . . . . . . . . . . . . . . . . . . .
T.4~r.a11h. ;1Ioiiieiitos extrenios de eiiipotramieiito perfecto en vigas con car-
tela en un extremo para carga uniforiiiemente repartida . . . . . . .