El documento describe cuatro métodos para resolver numéricamente la ecuación de advección unidimensional: el método upwind-upstream, el método FTCS, el método Lax-Friedrichs y el método de diferencias finitas. Explica que el método upwind-upstream es de orden dos, mientras que FTCS es más preciso pero inestable. También muestra código en Matlab para implementar los métodos y comparar sus resultados al aproximar una función senoidal transportada por el flujo.

1. Ecuación de Advección 1D
Cristian Quezada, Modelos Matemáticos de la Ciencia III 28/11/2016
1 Marco Teórico
1.1 Modelo de advección
La ecuación de advección es una ecuación diferencial parcial que muestra la variación de un
campo escalar en un punto dado por el efecto de un campo vectorial. Por ejemplo el transporte
de una sustancia contaminante que viaja por el caudal de un río. También en meteorología es
usada para modelar el efecto del transporte de una propiedad atmosférica, como la temperatura
o la humedad, por efecto del viento; al igual que en oceanografía se puede usar para modelar
el transporte de la salinidad por efecto de las corrientes marinas. La ecuación de advección es,
aunque no lo parezca, fácil de resolver analíticamente, pero su resolución numérica presenta una
gran dicultad de solución,esto se debe a que es una una ecuación diferencial parcial hiperbólica
Si una sustancia esta siendo transportada (o advectada) en un uido a una velocidad constante
u, entonces la función del ujo puede escribirse como
f(c) = uc
Entonces podemos saber el ujo de materia que pasa por el punto x simplemente multiplicando
la densidad local c(x, t) por la velocidad de transporte. Como el total de la masa que pasa entre
x1 y x2 cambia únicamente debido al ujo en los puntos nales, podemos calcularla como
d
dt
x2
x1
c(x, t)dx = f(c(x1, t) − c(x2, t)),
El signo menos de esta ecuación viene del hecho de que fes, por denición, el ujo a la derecha.
x2
x1
∂
∂t
c(x, t) +
∂
∂x
f(c(x, t)) dx = 0
y debido a que la integral tiene que ser igual a 0 para todos los valores de x1 y x2,entonces esto
quiere decir que el integrando es igual a 0, y con esto obtenemos la ecuación diferencial.
∂
∂t
c(x, t) +
∂
∂x
f(c(x, t)) = 0
Para el problema que estamos tratando, el transporte de una sustancia en un uido a una velocidad
constante, tenemos que f(c) = uc, donde u es una constante que representa la velocidad del uido.
Assignment 5 Page 1 / 9

2. Utilizando estos valores en la ecuación anterior obtenemos:
∂
∂t
c(x, t) + u
∂
∂x
c(x, t) = 0 (1)
Con la siguiente condición inicial:
c(x, 0) = v(x)
Teorema 1. La solución de la ecuación (1) es:
c(x, t) = v(x − ut) (2)
Es fácil vericar que esta ecuación satisface la ecuación de advección
1.2 Método upwind-upstream
Si hacemos la expansión en serie de Taylor alrededor del punto (xj, tn) obtenemos
c(xj, tn + ∆t) = c(xj, tn) +
∂c
∂t
(xj, tn)∆t + O(∆t2
)
Ahora cambiamos de notación y pondremos la variable temporal como superíndice y la espacial
como subíndice.
cn+1
j = cn
j +
∂c
∂t
(xj, tn
)∆t + O(∆t2
)
Despejamos la derivada:
∂c
∂t
(xj, tn
) =
cn+1
j − cn
j
∆t
+ O(∆t) (3)
Obtenemos una diferencia finita progresiva,ya que el término a la derecha es el instante superior,
si fuera el instante inferior sería regresiva(Mas detalle ver en referencia a Zill). Usando estas
diferencias finitas progresivas en la ecuacion (1), se llega al primer método.
cn+1
j = cn
j − u
∆t
∆x
(cn
j − cn
j−1) (4)
1.3 Método FTCS
Este usa el esquema de diferencias finitas centradas en la variable espacial.
∂c
∂x
(xj, tn
) =
cn
j+1 − cn
j−1
2∆x
+ O(∆t, ∆x2
)
cn+1
j = cn
j −
u
2
∆t
∆x
(cn
j+1 − cn
j−1) + O(∆t2
, ∆x2
, ∆t) (5)
Pero este método es inestable.
Assignment 5 Page 2 / 9

3. 1.4 Método Lax-Friedrichs
Una manera de tratar el problema de estabilidad del esquema FTCS fue propuesta por Lax y
Friedrichs. La idea básica es bastante simple y está basada en reemplazar, en el esquema FTCS,
el término cn
j por su promedio espacial.
cn+1
j =
1
2
(cn
j+1 + cn
j−1) −
u
2
∆t
∆x
(cn
j+1 − cn
j−1) + O(∆x2
) (6)
2 Código y pruebas - Matlab/Octave
2.1 Código Matlab
El siguiente código muestra los tre métodos para aproximar la ecuación de advección. Para este
caso se fijará el ejemplo con la ecuación:
c(x, t) = sin(x −
π
10
t),
sujeto a las condiciones iniciales, que es la misma ecuación cuando x = y cuando x = 2π que
se comprueba que satisface la ecuación (1) escogiendo la velocidad u = π
10
Código en Matlab:
1 %C r i s t i a n Quezada
2 clear ; c l c ; c l f ;
3 t i c ( ) ;
4 u = pi / 1 0 ; %v e l . del v i e n t o
5 L = 2∗ pi ; N = 81; T = 5; m = 1000;
6 dx = L /N; dt = T /m;
7 g=@( x , t ) sin ( x−pi /10∗ t ) ;
8
9 x = 0: dx : L ;
10 c0 = f ( x ) ;
11
12 c = c0 ;
13 temp = c ;
14 l = u∗ dt / dx ;
15
16 for j = 0:m
17 c ( 1 ) = g ( x ( 1 ) , j ∗ dt ) ;
18 c ( end ) = g ( x ( end ) , j ∗ dt ) ;
19 temp = c ;
20 for i =2:N
21 %temp ( i ) = (1− l )∗c ( i )+l ∗c ( i −1) ;
22 %temp ( i ) = c ( i ) −( l / 2 ) ∗c ( i +1)+( l / 2 ) ∗c ( i −1) ;
23 %temp ( i ) = 0.5∗( c ( i −1)+c ( i +1) ) −( l / 2 ) ∗c ( i +1)+( l / 2 ) ∗c ( i −1) ;
24 end
Assignment 5 Page 3 / 9

4. 25 c = temp ;
26 end
27
28 y = g ( x , 5 ) ;
29 plot ( x , y ) ;
30 hold on
31 plot ( x ( 1 :N) , c ( 1 :N) , ’ r ’ ) ;
32 %[ x ’ c ’ y ’ ]
33
34 elapsed_time = toc ( ) ;
35 f p r i n t f ( ’ se ␣demoro␣%4.4 f ␣ segundos ␣ n ’ , elapsed_time ) ;
Las lineas 21,22 y 23 estan comentadas, se debe quitar solo de una linea, dependiendo del
método que se desee probar.El primero es para el método upwind, el segundo la FTCS y el
último para el caso de Lax. Probaremos en todos los casos la aproximación de los métodos para
el tiempo t = 5.
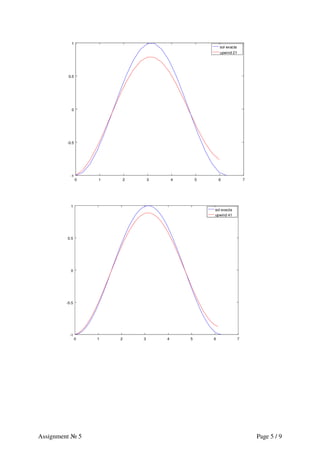
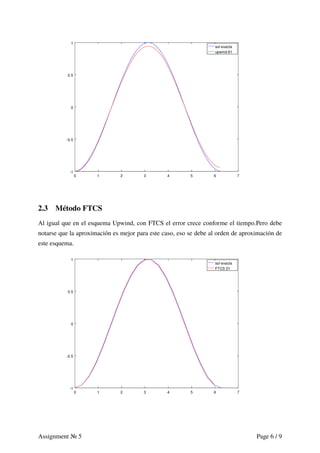
2.2 Método upwind-upstream
Mostraremos el caso para 21,41 y 81 nodos. La discretización de la región. Nótese que el error
crece conforme avanza el tiempo, esto se debe a dos factores:
• La calidad de aproximación del esquema: Hay que señalar que Upwind es un esquema de
orden dos.
• Discretización: Esto se puede mostrar señalando que los errores decrecen conforme se
aumenta el número de nodos en la discretización.
Assignment 5 Page 4 / 9

5. Assignment 5 Page 5 / 9

6. 2.3 Método FTCS
Al igual que en el esquema Upwind, con FTCS el error crece conforme el tiempo.Pero debe
notarse que la aproximación es mejor para este caso, eso se debe al orden de aproximación de
este esquema.
Assignment 5 Page 6 / 9

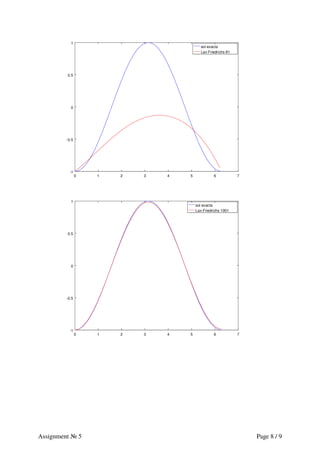
7. 2.4 Método Lax-Friedrichs
Debido a las condiciones para la estabilidad de este método, explicadas en el capítulo anterior,
la discretización en el espacio se hizo diferente para este ejemplo; el intervalo espacial [0, 2π]
se divide entonces en 1001, 2001 y 4001 puntos para cumplir con la condición de estabilidad.
Assignment 5 Page 7 / 9

8. Assignment 5 Page 8 / 9

9. 2.5 Conclusiones
El último método ofrece una mayor resolución debido a la gran cantidad de nodos y nos provee
mayor información, la única contra es su gran costo computacional, pero para los ordenadoras
de hoy no es gran problema.
Hecho en LATEX
References
[1] Luis Manuel Rivera. Solución numérica de la ecuación de advección empleando mallas
estructuradas sobre regiones planas irregulares utilizando un esquema de diferencias fini-
tas.(Tesis). UNIVERSIDAD MICHOACANA DE SAN NICOLÁS DE HIDALGO, 2014.
[2] Dennis Zill. Ecuaciones Diferenciales con problemas con valores en la frontera. (8va edi-
ción). Cengage, 2015.
Assignment 5 Page 9 / 9