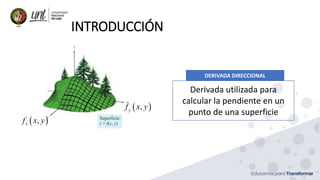
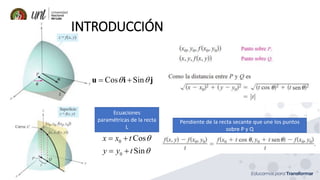
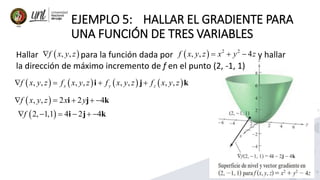
Este documento presenta conceptos sobre derivadas direccionales y gradientes para funciones de dos y tres variables. Introduce la definición de derivada direccional y gradiente. Presenta ejemplos de cómo calcular derivadas direccionales y gradientes para diferentes funciones. También cubre propiedades de los gradientes y cómo se aplican los conceptos a funciones de tres variables.

2. Cálculo Multivariable
Marcelo FernandoValdiviezo C.
Carrerade Telecomunicaciones
Octubre- 2020

3. UNIDAD3: INTEGRACIÓNVECTORIAL
TEMA: DERIVADAS DIRECCIONALES Y GRADIENTES.

4. INTRODUCCIÓN
 
,
x
f x y
 
,
y
f x y
DERIVADA DIRECCIONAL
Derivada utilizada para
calcular la pendiente en un
punto de una superficie

5. INTRODUCCIÓN
Cos Sin
 
 
u i j
0
0
Cos
Sin
x x t
y y t


 
 
Ecuaciones
paramétricas de la recta
L
Pendiente de la recta secante que une los puntos
sobre P y Q

6. DEFINICIÓN
DEFINICIÓN DE LA DERIVADA DIRECCIONAL

7. DEFINICIÓN
TEOREMA: DERIVADA DIRECCIONAL

8. EJEMPLO 1: HALLAR UNA DERIVADA
DIRECCIONAL
Hallar las derivadas direccional de en (1, 2) en la
dirección de
  2 2
1
, 4
4
f x y x y
  
     
, , Cos , Sin
x y
D f x y f x y f x y
 
 
u
Cos Sin
3 3
 
   
 
   
   
u i j
 
2 Cos Sin
2
y
x  
 
    
 
, 1, 2
3
x y

   
   
 
 
2
1,2 2 1 Cos Sin
3 2 3
D f
 
 
   
 
 
u
     
1 3 3
1,2 2 1 1 1.866
2 2 2
D f         
u

9. EJEMPLO 2: HALLAR UNA DERIVADA
DIRECCIONAL
Hallar las derivadas direccional de en en la
dirección de
  2
, Sin 2
f x y x y

     
, , Cos , Sin
x y
D f x y f x y f x y
 
 
u
3 4
 
v i j
   
2
2 Sin 2 Cos 2 Cos2 Sin
x y x y
 
 
   
3 4
1, 2Sin 2Cos
2 5 5
D f

 
   
  
   
   
u
1,
2

 
 
 
3 4
Cos Sin
5 5
 
    
v
u i j i j
v
   
3 4 8
1, 0 2
2 5 5 5
D f

   
    
   
   
u

10. GRADIENTE DE UNA FUNCIÓN DE DOS
VARIABLES
DEFINICIÓN DE GRADIENTE DE UNA FUNCIÓN DE DOS VARIABLES

11. EJEMPLO 3: HALLAR EL GRADIENTE DE
LA FUNCIÓN
Hallar el gradiente de en el punto (1, 2)
  2
, ln
f x y y x xy
 
 
 
2
,
, ln 2
x
y
y
f x y y
x
f x y x xy
 
 
   
2
, ln 2
y
f x y y x xy
x
 
    
 
 
i j
    
 
2
2
1,2 2 ln1 2 1 2
1
f
 
    
 
 
i j
 
1,2 6 4
f
  
i j

12. GRADIENTE DE UNA FUNCIÓN DE DOS
VARIABLES
FORMA ALTERNATIVA DE LA DERIVADA DIRECCIONAL

13. EJEMPLO 4: HALLAR UNA DERIVADA
DIRECCIONAL USANDO EL GRADIENTE
Hallar la derivada direccional de en en la
dirección de
  2 2
, 3 2
f x y x y
 
3
,0
4
 

 
 
 
3
,0 0,1
4
P a Q
 

 
 
 
3 3
0 1 0
4 4
PQ
 
      
 
 
v i j i j
3 4
5 5
  
v
u i j
v
     
 
, , ,
, 6 4
x y
f x y f x y f x y
f x y x y
  
  
i j
i j
 
3 3
,0 6 4 0
4 4
f
   
    
   
   
i j
3 9
,0 0
4 4
f
 
    
 
 
i j
3 3
,0 ,0
4 4
D f f
   
    
   
   
u u
3 9 3 4 27
,0 0
4 2 5 5 10
D f
     
       
     
     
u i j i j

14. PROPIEDADES DEL GRADIENTE
TEOREMA: PROPIEDADES DEL GRADIENTE

15. FUNCIONES DE TRES VARIABLES
DERIVADA DIRECCIONAL Y GRADIENTE PARA FUNCIONES DE TRES VARIABLES

16. FUNCIONES DE TRES VARIABLES
DERIVADA DIRECCIONAL Y GRADIENTE PARA FUNCIONES DE TRES VARIABLES

17. EJEMPLO 5: HALLAR EL GRADIENTE PARA
UNA FUNCIÓN DE TRES VARIABLES
Hallar para la función dada por y hallar
la dirección de máximo incremento de f en el punto (2, -1, 1)
 
, ,
f x y z
   2 2
, , 4
f x y z x y z
  
       
, , , , , , , ,
x y z
f x y z f x y z f x y z f x y z
   
i j k
 
, , 2 2 4
f x y z x y
    
i j k
 
2, 1,1 4 2 4
f
     
i j k

18. PREGUNTAS