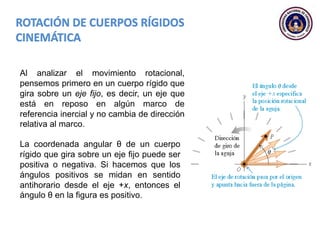
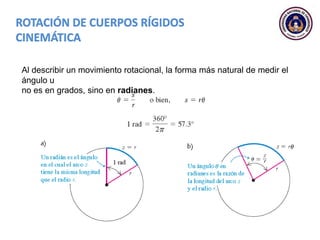
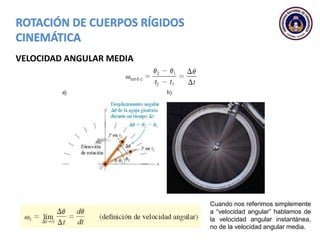
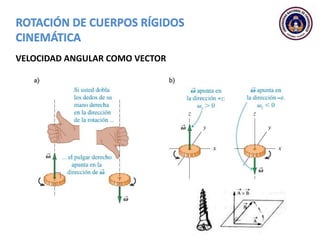
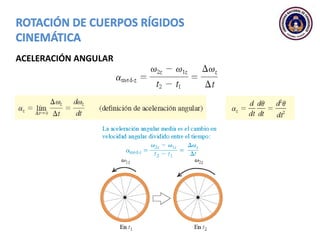
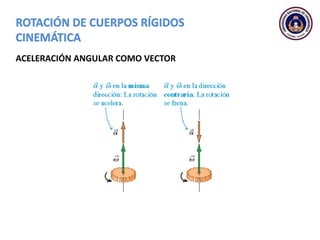
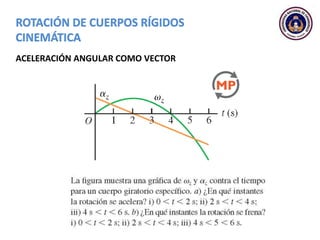
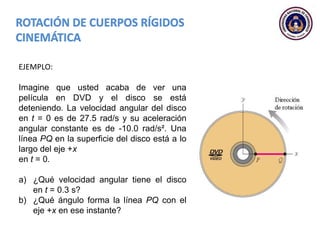
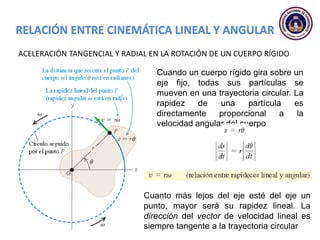
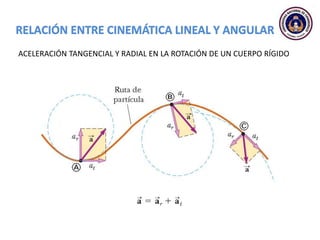
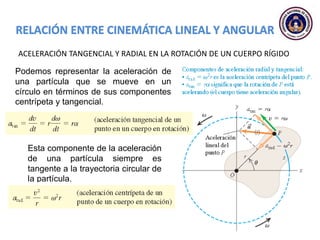
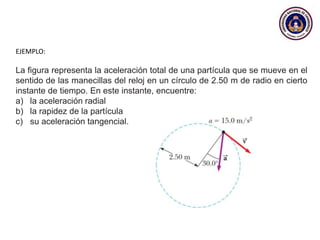
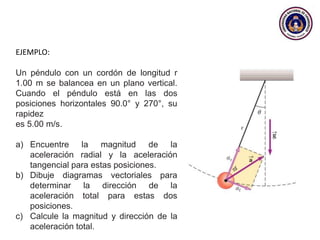
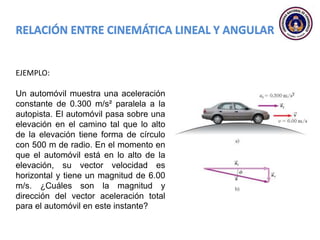
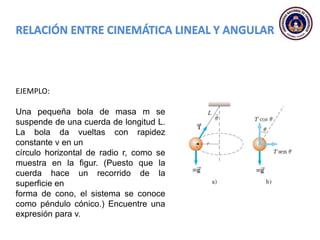
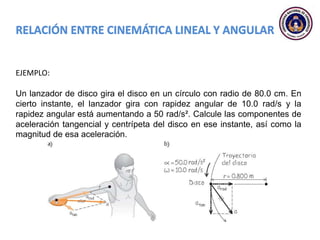
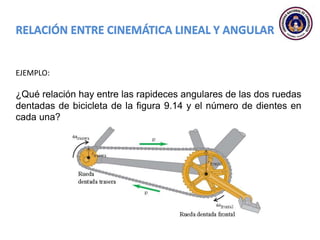
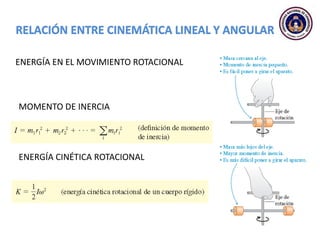
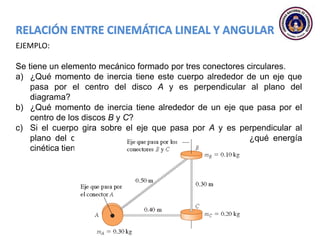
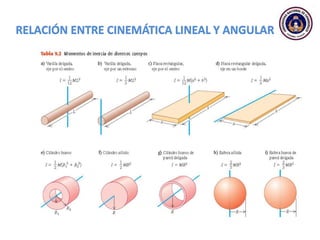
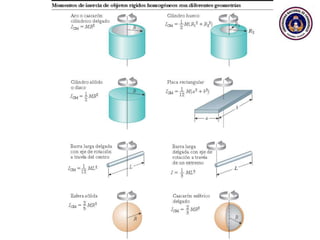
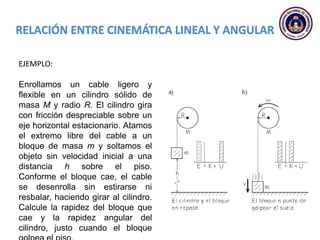
Este documento trata sobre el movimiento circular y rotacional. Explica conceptos como velocidad angular, aceleración angular, momento de inercia y energía cinética rotacional. Incluye ecuaciones y ejemplos para calcular estas cantidades para objetos que rotan sobre un eje fijo. También analiza la aceleración tangencial y radial de partículas en rotación y cómo se relacionan con la velocidad angular del cuerpo rígido.

1. UNIDAD: MOVIMIENTO CIRCULAR
CARRERA DE INGENIERIA AMBIENTAL
Periodo 2023 2S
Lenin Orozco Cantos

3. Al analizar el movimiento rotacional,
pensemos primero en un cuerpo rígido que
gira sobre un eje fijo, es decir, un eje que
está en reposo en algún marco de
referencia inercial y no cambia de dirección
relativa al marco.
La coordenada angular θ de un cuerpo
rígido que gira sobre un eje fijo puede ser
positiva o negativa. Si hacemos que los
ángulos positivos se midan en sentido
antihorario desde el eje +x, entonces el
ángulo θ en la figura es positivo.

4. Al describir un movimiento rotacional, la forma más natural de medir el
ángulo u
no es en grados, sino en radianes.

5. EJEMPLO:
Una rueda de bicicleta da 4.50 revoluciones.
¿Cuántos grados y radianes ha girado?

6. EJEMPLO:
El ojo de una ave particular apenas
puede distinguir los objetos que
subtienden un ángulo no menor de 3 ×
10−3
𝑟𝑎𝑑.
a) ¿Cuántos grados es esto?
b) ¿Cuán pequeño será el objeto que el
ave apenas pueda distinguir cuando
vuele a una altura de 100 m

7. VELOCIDAD ANGULAR MEDIA
Cuando nos referimos simplemente
a “velocidad angular” hablamos de
la velocidad angular instantánea,
no de la velocidad angular media.

8. VELOCIDAD ANGULAR MEDIA
Diferentes puntos de un cuerpo
rígido en rotación recorren
diferentes distancias en un tiempo
dado, dependiendo de la distancia
con respecto al eje de rotación.
No obstante, dado que el cuerpo
es rígido, todos los puntos giran el
mismo ángulo en el mismo
tiempo. Por lo tanto, en cualquier
instante, todas las partes de un
cuerpo rígido en rotación tienen la
misma velocidad angular.

9. VELOCIDAD ANGULAR MEDIA
En muchas situaciones es conveniente describir el movimiento de una
partícula que se mueve con rapidez constante en un círculo de radio r
en términos del periodo T, que se define como el intervalo de tiempo
requerido para una revolución completa de la partícula.
En el intervalo de tiempo T, la partícula se mueve una distancia de 2𝜋𝑟,
que es igual a la circunferencia de la trayectoria circular de la partícula.
En consecuencia, puesto que su rapidez es igual a la circunferencia de
la trayectoria circular dividida entre el periodo:
𝜔 =
2𝜋𝑟
𝑇
𝑇 =
2𝜋𝑟
𝜔
𝑇 =
1
𝑓

10. VELOCIDAD ANGULAR COMO VECTOR

11. ACELERACIÓN ANGULAR

12. ACELERACIÓN ANGULAR COMO VECTOR

13. ACELERACIÓN ANGULAR COMO VECTOR

14. VELOCIDAD ANGULAR MEDIA
EJEMPLO:
El volante de un automóvil prototipo se somete a prueba. La posición
angular θ del volante está dada por
El diámetro del volante es de 0.36 m.
a) Calcule el ángulo θ, en radianes y en grados, en t1 = 2.0 s y t2 = 5.0 s.
b) Calcule la distancia que recorre una partícula en el borde durante ese
intervalo.
c) Calcule la velocidad angular media, en rad/s y en rev/min (rpm), entre t1
= 2.0 s y t2 = 5.0 s.
d) Calcule la velocidad angular instantánea al t = t2 = 5.0 s.

15. ROTACIÓN CON ACELERACIÓN ANGULAR CONSTANTE

16. EJEMPLO:
Imagine que usted acaba de ver una
película en DVD y el disco se está
deteniendo. La velocidad angular del disco
en t = 0 es de 27.5 rad/s y su aceleración
angular constante es de -10.0 rad/s². Una
línea PQ en la superficie del disco está a lo
largo del eje +x
en t = 0.
a) ¿Qué velocidad angular tiene el disco
en t = 0.3 s?
b) ¿Qué ángulo forma la línea PQ con el
eje +x en ese instante?

17. Cuando un cuerpo rígido gira sobre un
eje fijo, todas sus partículas se
mueven en una trayectoria circular. La
rapidez de una partícula es
directamente proporcional a la
velocidad angular del cuerpo
Cuanto más lejos del eje esté del eje un
punto, mayor será su rapidez lineal. La
dirección del vector de velocidad lineal es
siempre tangente a la trayectoria circular
ACELERACIÓN TANGENCIAL Y RADIAL EN LA ROTACIÓN DE UN CUERPO RÍGIDO

18. ACELERACIÓN TANGENCIAL Y RADIAL EN LA ROTACIÓN DE UN CUERPO RÍGIDO

19. ACELERACIÓN TANGENCIAL Y RADIAL EN LA ROTACIÓN DE UN CUERPO RÍGIDO
Podemos representar la aceleración de
una partícula que se mueve en un
círculo en términos de sus componentes
centrípeta y tangencial.
Esta componente de la aceleración
de una partícula siempre es
tangente a la trayectoria circular de
la partícula.

20. EJEMPLO:
La figura representa la aceleración total de una partícula que se mueve en el
sentido de las manecillas del reloj en un círculo de 2.50 m de radio en cierto
instante de tiempo. En este instante, encuentre:
a) la aceleración radial
b) la rapidez de la partícula
c) su aceleración tangencial.

21. EJEMPLO:
Una bicicleta frena uniformemente desde v= 8.40 m/s hasta el reposo en una
distancia de 115 m. Cada rueda y llanta tienen un diámetro global de 68.0
cm. Determine:
a) la velocidad angular de las ruedas en el instante inicial (t = 0)
b) el número total de revoluciones que cada rueda completa antes de llegar
al reposo
c) la aceleración angular de la rueda
d) el tiempo que le toma llegar a detenerse.

22. EJEMPLO:
Un péndulo con un cordón de longitud r
1.00 m se balancea en un plano vertical.
Cuando el péndulo está en las dos
posiciones horizontales 90.0° y 270°, su
rapidez
es 5.00 m/s.
a) Encuentre la magnitud de la
aceleración radial y la aceleración
tangencial para estas posiciones.
b) Dibuje diagramas vectoriales para
determinar la dirección de la
aceleración total para estas dos
posiciones.
c) Calcule la magnitud y dirección de la
aceleración total.

23. EJEMPLO:
¿Cuál es la aceleración centrípeta de la Tierra a medida que se mueve en
su órbita alrededor del Sol?

24. EJEMPLO:
Un automóvil muestra una aceleración
constante de 0.300 m/s² paralela a la
autopista. El automóvil pasa sobre una
elevación en el camino tal que lo alto
de la elevación tiene forma de círculo
con 500 m de radio. En el momento en
que el automóvil está en lo alto de la
elevación, su vector velocidad es
horizontal y tiene un magnitud de 6.00
m/s. ¿Cuáles son la magnitud y
dirección del vector aceleración total
para el automóvil en este instante?

25. EJEMPLO:
Una pequeña bola de masa m se
suspende de una cuerda de longitud L.
La bola da vueltas con rapidez
constante v en un
círculo horizontal de radio r, como se
muestra en la figur. (Puesto que la
cuerda hace un recorrido de la
superficie en
forma de cono, el sistema se conoce
como péndulo cónico.) Encuentre una
expresión para v.

26. EJEMPLO:
Un lanzador de disco gira el disco en un círculo con radio de 80.0 cm. En
cierto instante, el lanzador gira con rapidez angular de 10.0 rad/s y la
rapidez angular está aumentando a 50 rad/s². Calcule las componentes de
aceleración tangencial y centrípeta del disco en ese instante, así como la
magnitud de esa aceleración.

27. EJEMPLO:
¿Qué relación hay entre las rapideces angulares de las dos ruedas
dentadas de bicicleta de la figura 9.14 y el número de dientes en
cada una?

28. ENERGÍA EN EL MOVIMIENTO ROTACIONAL
Un cuerpo rígido en rotación es una masa en movimiento, así que tiene
energía cinética que podemos expresar en términos de la rapidez angular
del cuerpo y una nueva cantidad llamada momento de inercia, que
depende de la masa del cuerpo y de la forma en que se distribuye tal
masa.
Cuando un cuerpo rígido gira sobre un eje fijo, la energía cinética de la i-
ésima partícula es:
MOMENTO
DE INERCIA

29. ENERGÍA EN EL MOVIMIENTO ROTACIONAL
MOMENTO DE INERCIA
ENERGÍA CINÉTICA ROTACIONAL

30. EJEMPLO:
Se tiene un elemento mecánico formado por tres conectores circulares.
a) ¿Qué momento de inercia tiene este cuerpo alrededor de un eje que
pasa por el centro del disco A y es perpendicular al plano del
diagrama?
b) ¿Qué momento de inercia tiene alrededor de un eje que pasa por el
centro de los discos B y C?
c) Si el cuerpo gira sobre el eje que pasa por A y es perpendicular al
plano del diagrama, con rapidez angular 𝜔 = 4 𝑟𝑎𝑑/𝑠, ¿qué energía
cinética tiene?

31. EJEMPLO:
Cuatro esferas pequeñas se amarran a los
extremos de dos barras con masa despreciable
que yacen en el plano xy. Se supondrá que los
radios de las esferas son pequeños en
comparación con las dimensiones de las barras.
A) Si el sistema da vueltas en torno al eje y con una
rapidez angular 𝜔, encuentre el momento de
inercia y la energía cinética rotacional del sistema
en torno a este eje.
B) Suponga que el sistema da vueltas en el plano xy
en torno a un eje (el eje z) a través de O. Calcule
el momento de inercia y la energía cinética
rotacional en torno a este eje.

34. PREGUNTA RÁPIDA:
Una sección de tubería hueca y un cilindro sólido tienen los
mismos radio, masa y longitud. Ambos dan vueltas en torno
a su largo eje central con la misma rapidez angular. ¿Cuál
objeto tiene la mayor energía cinética rotacional?:
a) La tubería hueca.
b) El cilindro sólido.
c) Tienen la misma energía cinética rotacional.
d) Es imposible de determinar.

35. PREGUNTA RÁPIDA:
Una sección de tubería hueca y un cilindro sólido tienen los
mismos radio, masa y longitud. Ambos dan vueltas en torno
a su largo eje central con la misma rapidez angular. ¿Cuál
objeto tiene la mayor energía cinética rotacional?:
a) La tubería hueca.
b) El cilindro sólido.
c) Tienen la misma energía cinética rotacional.
d) Es imposible de determinar.
Casi toda la masa de la tubería esta a la misma distancia
del eje de rotación, de modo que tiene un momento de
inercia mas grande que el cilindro solido.

36. EJEMPLO:
Enrollamos un cable ligero y
flexible en un cilindro sólido de
masa M y radio R. El cilindro gira
con fricción despreciable sobre un
eje horizontal estacionario. Atamos
el extremo libre del cable a un
bloque de masa m y soltamos el
objeto sin velocidad inicial a una
distancia h sobre el piso.
Conforme el bloque cae, el cable
se desenrolla sin estirarse ni
resbalar, haciendo girar al cilindro.
Calcule la rapidez del bloque que
cae y la rapidez angular del
cilindro, justo cuando el bloque