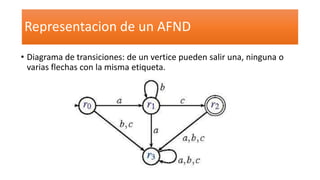
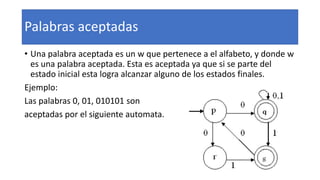
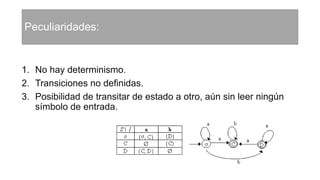
1) Los automatas finitos no deterministas generalizan a los deterministas al permitir más de una computación alternativa en la misma cadena de entrada. 2) Se diferencian de los deterministas en que permiten más de un estado sucesor y transiciones sin consumir símbolos. 3) El lenguaje aceptado por un AFND incluye todas las cadenas que puedan llevar al automata a un estado final.

1. Autómata Finito
No-Deterministico
Joan Vidal 13-0980
Luis Martinez 13-0219

2. Breve recuento
Una extension a los automatas finitos deterministas es la de permitir
que de cada nodo del diagrama de estados salga un numero de flechas
mayor o menor.
• Permitir que falten flechas
correspondiente a los simbolos del
alfabeto
• Existencia de varias flechas de un
solo nodo
• Permite transiciones con etiquetas
de varias letras
AFND
Las restricciones de los AFN
es menor que los AFD,
resulta que los AFD son un
caso particular de los AFND,
por lo que todo AFD es de
hecho un AFND.

3. • Los Automatas Finitos se generalizan al anadirseles lo no-deterministico, lo
que permite varias computaciones alternativas en la misma cadena de
entrada.
• Los Automatas Finitos deterministicos ordinarios siguen una ruta en cada
entrada.
• Dos cambios:
-Permitir a la funcion de transferencia δ (q, a) especificar mas de un estado
sucesor.
- Generar transiciones con el elemento ε, transiciones gratuitas, sin consumir
ningun simbolo de entrada.

4. Definicion Formal de un Automata Finito
No-Deterministico (AFND)
Un AFND esta compuesto por el quinteto: (Q, Σ, δ, q0, F) en donde:
• Q es un conjunto finito de estados,
• Σ es un conjunto finito de simbolos de entrada, tambien se conoce como Alfabeto del
Automata.
• δ: Q × Σε, es decir P(Q) es una funcion de tranferencia.
• q0 ∈Q, es el estado inicial.
• F ⊆ Q, es el conjunto de estados finales.
El numero de estados en P(Q) se puede deteminar por 2^|Q|.
Ejemplo: Sea Q = {a, b, c}
P(Q) = { ∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}

5. Lenguaje aceptado por un AFND
El lenguaje aceptado por un AFND es el conjunto de todas las cadenas
de simbolos terminales que pueden hacer que el AFND llegue a un
estado final de aceptacion. Para llegar a una definicion formal de este
lenguaje ampliaremos la definicion de la funcion de transicion con
objeto de que acepte cadenas de caracteres. Es decir, si la funcion de
transicion de un AFND de define ası: f : Q∗Σ → 2^Q.
Una vez ampliada su definicion, el lenguaje aceptado por el AFND
es: L(AF ND) = {x ∈ Σ∗/f''(q0, x)∩F != Ø}

6. Representacion de un AFND
• Diagrama de transiciones: de un vertice pueden salir una, ninguna o
varias flechas con la misma etiqueta.

7. Representacion de un AFND
• Tabla de transiciones: se emplea un tabla donde la columna son el
alfabeto mientras que las filas representan los diferentes estados, y el
contenido de columna-fila es el estado siguiente a donde este pasa.

8. Palabras aceptadas
• Una palabra aceptada es un w que pertenece a el alfabeto, y donde w
es una palabra aceptada. Esta es aceptada ya que si se parte del
estado inicial esta logra alcanzar alguno de los estados finales.
Ejemplo:
Las palabras 0, 01, 010101 son
aceptadas por el siguiente automata.

9. Peculiaridades:
1. No hay determinismo.
2. Transiciones no definidas.
3. Posibilidad de transitar de estado a otro, aún sin leer ningún
símbolo de entrada.

10. Implementacion
Hay muchas formas de implementar una AFND:
• Convertir al equivalente AFD: en algunos casos esto puede causar una explosión exponencial
en el tamaño del autómata, y así un espacio auxiliar proporcional al número de estados en el
AFND.
• Mantener un conjunto de datos de todos los estados en que la máquina podría estar en la
actualidad. Al consumir el último carácter de entrada, si uno de estos estados es un estado
final, la máquina acepta la cadena. En el peor de los casos, esto puede requerir espacio
adicional proporcional al número de estados en el AFND; si la estructura del conjunto usa un
bit por estado del AFND, entonces esta solución es exactamente equivalente a la anterior.
• Crear múltiples copias. Por cada n forma de la decisión, el AFND crea hasta n-1 copias de la
máquina. Cada uno de ellos entrara en un estado independiente. Si, al momento de consumir
el último símbolo de la entrada, al menos una copia del AFND esta en un estado de aceptación,
el AFND lo aceptará. (Esto también requiere un almacenamiento lineal con respecto al número
de estados del AFND, ya que puede haber una máquina por cada estado del AFND).

11. Ejemplos

12. Ejemplo:

13. Referencias
http://www2.dis.ulpgc.es/~mluengo/automatas/teoria/tema2.pdfhttp://campusvir
tual.unex.es/ebooks/files/file/TeoriaAutomatas.pdf
http://users.dsic.upv.es/asignaturas/eui/alc/AF.pdf
http://luzem.dyndns.org/tag/automata-finito-no-determinista-a-automata-finito-
determinista/
http://trevinca.ei.uvigo.es/~formella/doc/talf05/talf/node21.html
http://datateca.unad.edu.co/contenidos/301405/EXEMODULO20131/exe%20modu
lo%20301405/leccin_8__autmatas_finitos_no_determinsticos_afnd.html
http://webdiis.unizar.es/asignaturas/TC/wp/wp-
content/uploads/2012/09/121001NFAI1.pdf
http://virtual.unibe.edu.do/file.php?file=%2F712%2FMIT6_045JS11_lec03.pdf