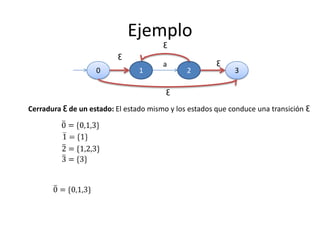
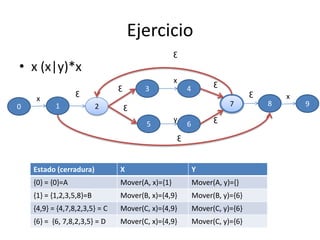
Este documento describe el proceso de convertir expresiones regulares a autómatas finitos deterministas (AFD). Explica cómo las expresiones regulares se pueden representar como autómatas finitos no deterministas (AFND) y luego cómo convertir un AFND a un AFD usando el algoritmo de cerradura epsilon y la construcción de subconjuntos. También incluye ejemplos para ilustrar estos pasos y ejercicios prácticos para construir AFD a partir de AFND.

1. DESDE LAS EXPRESIONES
REGULARES HASTA LOS AFD

2. EXPRESIÓN REGULAR
AFND
AFD

3. ER - AFND
• CONCATENACIÓN (a.b)
1
3
a
b
2
1
a
2
Ɛ
b
3
4
4
• Selección (a|b)
1
3
a
b
2
Ɛ
0
4
Ɛ
1
3
a
b
2
4
Ɛ
Ɛ
5

4. ER - AFND
• Repetición a*
Ɛ
Ɛ
0
1
a
Ɛ
2
Ɛ
3

5. DESDE UN AFND - AFD
Algoritmo

6. Ejemplo
Ɛ
Ɛ
0
1
a
2
Ɛ
3
Ɛ
Cerradura Ɛ de un estado: El estado mismo y los estados que conduce una transición Ɛ

7. Ejemplo
Ɛ
Ɛ
0
1
a
Ɛ
2
3
Ɛ
Construcción de subconjuntos :
1. El estado inicial es el mismo,
2. Cual de los estados conduce con un carácter
1 hacia el 2 = {1,2,3}
3. Desde los estados de {1,2,3} conducen con “a” hacia sí mismo
4. El estado de aceptación contiene el estado de aceptación del AFND
a
a

8. Ejercicio
Ɛ
1
a
2
3
Ɛ
b
4
Ɛ
5
Ɛ
8
Ɛ
a
6
7
Estado (cerradura)
a
b
{1} = {1,2,6}=A
Mover(A, a)={3,7}
Mover(A, b)={}
{3,7} = {3,4,7,8}=B
Mover(B, a)={}
Mover(B, b)={5}
{5} = {5,8} = C
Mover(C, a)={}
Mover(C, b)={}
Estado
(cerradura)
a
A
B
B (aceptación)
C (aceptación)
b
A
C
a
b
B
C

9. Ejercicio
Ɛ
• x (x|y)*x
x
0
Ɛ
Ɛ
1
x
2
Ɛ
4
3
Ɛ
7
Ɛ
5
y
Ɛ
6
Ɛ
Estado (cerradura)
X
Y
{0} = {0}=A
Mover(A, x)={1}
Mover(A, y)={}
{1} = {1,2,3,5,8}=B
Mover(B, x)={4,9}
Mover(B, y)={6}
{4,9} = {4,7,8,2,3,5} = C
Mover(C, x)={4,9}
Mover(C, y)={6}
{6} = {6, 7,8,2,3,5} = D
Mover(C, x)={4,9}
Mover(C, y)={6}
8
x
9

10. Ejercicio
• x (x|y)*x
Estado (cerradura)
X
Y
{0} = {0}=A
Mover(A, x)={1}
Mover(A, y)={}
{1} = {1,2,3,5,8}=B
Mover(B, x)={4,9}
Mover(B, y)={6}
{4,9} = {4,7,8,2,3,5,9} = C Mover(C, x)={4,9}
Mover(C, y)={6}
{6} = {6, 7,8,2,3,5} = D
Mover(C, y)={6}
Mover(C, x)={4,9}
X
X
A
B
Y
Estado
A
X
D
Y
Y
B
B
C
X
C
D
C
X
Y
C
D
D
C
D

11. ANÁLISIS SINTÁCTICO

12. ANÁLISIS SINTÁCTICO
• Su sintaxis se determina por: Reglas
gramaticales de una gramática libre de
contexto
• Operaciones son similares a las expresiones
regulares. Con la diferencia de que se debe
implementar la recursidad (ciclos repetitivos)
• Estructura de datos: árboles
• Algoritmo: Análisis sintáctico ascendente y
descendente

13. Gramáticas libres de contexto
• Es una especificación para la estructura
sintáctica de un lenguaje de programación
• Similar a la estructura léxica reflejada en la
expresión regular, solamente que la gramática
incluye recursividad