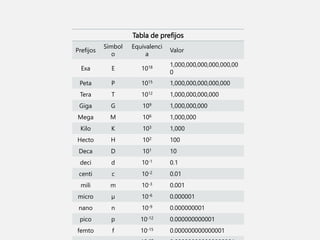
Este documento explica la notación científica, la cual permite escribir números muy grandes o pequeños usando exponentes de 10. En la notación científica, los números se escriben como el producto de un coeficiente y una potencia de 10. El exponente indica cuántos lugares se mueve el punto decimal. Se proveen ejemplos de cómo convertir entre notación decimal y científica, así como realizar operaciones básicas con números en notación científica.

1. Notación
científica.

2. NOTACIÓN CIENTÍFICA
Existen numerosos contextos donde aparecen números
muy grandes o muy pequeños. Las masas de los astros, las
distancias interestelares... son cantidades muy grandes; el
peso de los átomos, el diámetro de un glóbulo rojo... son
cantidades muy pequeñas.
Para trabajar con ellos utilizamos la notación científica. En
ella tienen gran importancia las potencias de 10. (10, 100,
1000, 10000, 100000…)

3. Notación científica.
Un numero escrito en notación científica sigue el siguiente patrón:
𝑚 𝑥10𝑛
Donde:
𝒎: se denomina coeficiente (esta debe de ser mayor o igual que 1 y
menor que 10).
𝒏: orden de la magnitud dada como exponente. (Potencia)
El exponente 𝑛, indica el espacio que se mueve el punto decimal
hasta colocarlo enseguida del primer digito diferente a cero.
Nota: Se puede poner 𝑥 o simplemente un punto

4. Si la coma decimal la mueves a la izquierda el exponente es
positivo, si lo mueves a la derecha el exponente es negativo.
5000 = 5 x 103
3 lugares a la izquierda = exponente
+3
0.006 = 6 x 10-3
3 lugares a la derecha = exponente
-3
Ejemplos
1) 90000 = 9 x 104
2) 0,0008 = 8 x 10-4
3) 8400000 = 8,4 x 106
4) 0,00000099 = 9,9 x 10-7
Notación
científica.

5. Cambio de exponente
1. 53,2 X 105 = 5,32 X 106 (El punto se recorre un lugar a la
izquierda, al exponente se le suma 1)
2. 28400 X 10–6 = 2.84 X 10–2 (El punto se recorre 4 lugares a la
izquierda, al exponente se le suma 4
3. 0.0000067 X 104 = 6.7 X 10–2 (El punto se recorre 6 lugares a la b
derecha, al exponente se le resta 6)
4. 0.000749 X 10–5 = 7.49 X 10–9 (El punto se recorre 4 lugares a la
derecha, al exponente se le resta 4)
Los números que están en notación científica se les
pueden modificar el exponente con las reglas de recorrido
del punto o la coma decimal:
https://www.matesfacil.com/ESO/numeros/notacion_cientifica/teoria-ejemplos-
numeros-decimales-exponente-positivo-negativo-base-10-test.html

6. Ejercicios
Convierte los siguientes números escritos en notación
decimal a notación científica:
1)50000 =
2)840 =
3)0.0093 =
4)2497.87 =
5)0.725 =
6) 435000000 =
7) 84065000=
8)285.2 =
9)0.0123 =
10) 0.000032 =
Convierte los siguientes números a notación
decimal:
1) 3𝑥106=
2) 4.5𝑥103=
3) 8,63𝑥105
=
4) 2,845𝑥10−5=
5) 1,83𝑥10−3=
6) 89,21𝑥10−2=
7) 78,23𝑥102
=
8) 328,76𝑥10−3
=
9) 2,345𝑥104=
10) 34𝑥10−6
=

7. Ejemplos de operaciones con notación científica
(10−4
)(105
) = 10−4+5
= 101
= 10
2𝑥108 3𝑥10−7 = 6𝑥108−7 = 6𝑥101 = 6 𝑥 10 = 60
106 10−6 = 106−6 = 100 = 1
4.2𝑥109 3.6𝑥10−4 = 15.12𝑥109−4 = 15.12𝑥105 = 1.512𝑥106
6.5𝑥106
9.8𝑥1014 = 0.66326𝑥106−14
= 0.66326𝑥10−8
= 6.6326𝑥10−9
2.5𝑥105 3 = 15.625𝑥105∗3 = 15.625𝑥1015 = 1.5625𝑥1016
3
125𝑥1015 = 5𝑥10
15
3 = 5𝑥105

8. Para sumar o restar números con potencia diez, hay que
asegurarse que los exponentes sean iguales.
Ejemplo: para sumar 2𝑥102 + 3𝑥103
1. Convertimos 2𝑥102 𝑎 0,2𝑥103 (se recorre el punto un lugar a la
izquierda y al exponente se le
suma 1)
2. Ahora los dos números tienen la misma potencia y se pueden
sumar. Sumamos los coeficientes y se coloca la misma
potencia.
0,2𝑥103
+ 3𝑥103
= 3,2𝑥103
Suma y resta

9. También se puede convertir el segundo numero en vez del
primero:
2𝑥102 + 3𝑥103
1. 3𝑥103 = 30𝑥102 (se recorre el punto un lugar a la derecha
y el exponente se le resta 1)
2. Ahora se pueden sumar:
2𝑥102 + 30𝑥102 = 32𝑥102 = 3,2𝑥103
Ejemplos:
1,3𝑥105 + 2𝑥103
= 1,3𝑥105 + 0,02𝑥105
= 1,32𝑥105
Suma y resta

10. También se puede convertir el segundo numero en vez del
primero:
2𝑥102 + 3𝑥103
1. 3𝑥103 = 30𝑥102 (se recorre el punto un lugar a la derecha
y el exponente se le resta 1)
2. Ahora se pueden sumar:
2𝑥102 + 30𝑥102 = 32𝑥102 = 3,2𝑥103
Ejemplos:
4.35𝑥10−6
− 3.5𝑥10−7
= 4.35𝑥10−6 − 0.35𝑥10−6
= 4𝑥10−6
Suma y resta

11. Para multiplicar números en notación científica basta con
multiplicar los coeficientes y sumar los exponentes.
4𝑥105 × 9𝑥102
1. 4 × 9 = 36 (se multiplican los coeficientes)
2. 5 + 2 = 7 (se suman los exponentes)
4𝑥105 × 9𝑥102 = 36𝑥107
Multiplicación

12. Para dividir números en notación científica basta con dividir los
coeficientes y restar los exponentes.
15𝑥106 ÷ 3𝑥103
1. 15 ÷ 3 = 5 (se dividen los coeficientes)
2. 6 − 3 = 3 (se restan los exponentes)
15𝑥106 ÷ 3𝑥103 = 5𝑥103
División

13. En los siguientes problemas , reduce y expresa el resultado
como un solo número escrito en notación científica.
1) (3000)(17000000)=
2) 4𝑥10−3 6𝑥10−7 =
3) 7𝑥1015
3𝑥10−9
=
4) 3𝑥10−3
6𝑥10−8 2
=
Ejercicios
5)
3𝑥106 9𝑥10−9 2
4𝑥10−5 =
6) 3𝑥106 9𝑥1017 =
7) 12𝑥105
+ 233𝑥102
=
8) 6.73𝑥10−6
− 2.31𝑥10−7
=

14. Tabla de prefijos
Prefijos
Símbol
o
Equivalenci
a
Valor
Exa E 1018 1,000,000,000,000,000,00
0
Peta P 1015 1,000,000,000,000,000
Tera T 1012 1,000,000,000,000
Giga G 109 1,000,000,000
Mega M 106 1,000,000
Kilo K 103 1,000
Hecto H 102 100
Deca D 101 10
deci d 10-1 0.1
centi c 10-2 0.01
mili m 10-3 0.001
micro µ 10-6 0.000001
nano n 10-9 0.000000001
pico p 10-12 0.000000000001
femto f 10-15 0.000000000000001