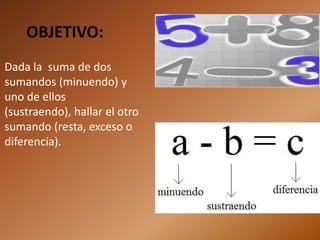
Este documento presenta los conceptos y operaciones básicas de la resta. Explica las leyes de la resta como la ley de uniformidad y la ley de monotonía. Luego, describe cómo realizar operaciones indicadas de suma y resta siguiendo las propiedades de estas operaciones, incluyendo sumar y restar números, sumas y diferencias indicadas. Finalmente, presenta algunos casos particulares como que la suma de dos números más su diferencia es igual al doble del mayor.

1. TRABAJO:
RESTA O SUSTRACCIÓN
PROFESOR:
JOSÉ CALIXTO SALAS GONZÁLEZ
SEMESTRE: ESPECIALIDAD:
3° MATEMÁTICAS

2. OBJETIVO:
Dada la suma de dos
sumandos (minuendo) y
uno de ellos
(sustraendo), hallar el otro
sumando (resta, exceso o
diferencia).

3. Pruebas:
2) Restando la
1) Sumando el diferencia del
sustraendo con la minuendo, debiend
diferencia, debiend o ser el sustraendo
o dar el minuendo.
15,200 15,200
93,254 58,076 13,896 1,304
58,076 35,178 1,304 13,896
35, 178 93,254

4. REPRESENTACIÓN GRAFICA.
7
A B
4
C D

5. Leyes de la resta:
Ley de uniformidad: La diferencia de dos números tiene
un valor único o siempre es igual.
11 – 3 = 8 únicamente por que 8 es el único número que
sumado con 3 da 11.
Restando miembro a miembro dos igualdades resulta otra
igualdad.
a=3
5=b
a-5=3-b

6. Leyes de la resta:
Ley de uniformidad: La diferencia de dos números tiene
un valor único o siempre es igual.
11 – 3 = 8 únicamente por que 8 es el único número que
sumado con 3 da 11.
Restando miembro a miembro dos igualdades resulta otra
igualdad.
a=3
5=b
a-5=3-b

7. Ley de monotonía: consta de tres partes.
1) Si una desigualdad (minuendo) se resta una igualdad
(sustraendo), siempre que la resta se pueda efectuar
resulta una desigualdad del mismo sentido que la
desigualdad minuendo.
8>5
2=2
8-2>5-2
6>3

8. 2) Si una desigualdad (minuendo) se resta una
igualdad (sustraendo), siempre que la resta se pueda
efectuar resulta una desigualdad de sentido contrario
que la desigualdad sustraendo.
9=9
5>3
9-5<9-3
4<6

9. 3) Si una desigualdad se resta otra desigualdad
de sentido contrario, siempre que la resta sea
posible, resulta una desigualdad del mismo
sentido que la desigualdad del minuendo.
7>4
2<3
7-2>4-3
5>1

10. Alteraciones del minuendo y el
sustraendo.
1) Si el minuendo aumenta o disminuye un número
cualquiera y el sustraendo no varía, la diferencia queda
aumentada o disminuida en el mismo número.
9-7=2
(9+3)-7=2 + 3
12-7= 5

11. 2) Si el sustraendo aumenta o disminuye un número
cualquiera y el minuendo no varía, la diferencia
disminuye en el primer caso y aumenta en el
segundo el mismo número.
10-3=7
10-(3+5)= 7 – 5
10-8= 2

12. 3) Si el minuendo y el sustraendo aumenta
o disminuyen a la vez un mismo número, la
diferencia no varía.
15-6=9
(15+2)-(6+2)=9
17-8=9

13. TRABAJO:
RESTA O SUSTRACCIÓN
PROFESOR:
JOSÉ CALIXTO SALAS GONZÁLEZ
SEMESTRE: ESPECIALIDAD:
3° MATEMÁTICAS

14. Operaciones
indicadas de suma
y LUEGO BAJO UN ASPECTO TEÓRICO.
resta …
SE VERÁN LAS OPERACIONES INDICADAS DE SUMA Y RESTA PRIMERO DESDE UN
PUNTO DE VISTA PRACTICO Y
Practica … OPERACIONES SIN SIGNO DE
AGRUPACIÓN
ESTAS OPERACIONES SE EFECTÚAN EN EL ORDEN QUE SE HALLAN
5+4-3+2 =
5+4= 9; 9-3= 6; 6+2= 8

15. Operaciones
indicadas de suma
y resta …
Operaciones en que hay signos de
agrupación..
LAS OPERACIONES CERRADAS DENTRO DE LOS PARÉNTESIS, HASTA
CONVERTIRLAS EN UN SOLO NUMERO Y LUEGO EFECTUAR LAS OPERACIONES
QUE QUEDEN INDICADAS.
SE EFECTÚAN PRIMERO LAS OPERACIONES ENCERRADAS ENTRE LOS PARÉNTESIS.
(7-2) + (5+4) –(3-2) =

16. Operaciones
indicadas de suma
y resta …
teoría …
ESTUDIAREMOS AHORA EL MÉTODO DE EFECTUAR LAS
OPERACIONES INDICADAS DE SUMA Y RESTA, FUNDADO EN LAS
PROPIEDADES DE LA SUMA Y LA RESTA. ES NECESARIO CONOCER
ESTE MÉTODO PORQUE SI LAS CANTIDADES ESTÁN REPRESENTADAS
POR LETRAS NO PODEMOS EFECTUAR LAS OPERACIONES
ENCERRADAS EN LOS PARÉNTESIS Y POR TANTO NO SE PUEDE
APLICAR EL MÉTODO EXPLICADO ANTERIORMENTE.

17. Operaciones
indicadas de suma
suma … y resta …
Suma de un numero y una suma indicada.
Para sumar un numero con una suma indicada el numero con uno cualquiera de los
sumandos de la suma.
Sea la operación (2+3+4)+5, decimos que :
(2+3+4 )+5=2+(3+5)+4=14
En efecto: al sumar el numero 5 con el sumando 3, la suma
(2+3+4) queda aumentada en unidades porque si un sumando se aumenta en un numero
cualquiera la suma queda aumentada en dicho numero.

18. Operaciones
indicadas de suma
y resta …
Suma de dos sumas indicadas
PARA SUMAR DOS SUMAS INDICADAS SE SUMAN TODOS LOS
SUMANDOS QUE LA FORMAN .
SEA LA OPERACIÓN (5+6) +(7+8), DECIMOS QUE:
(5+6)+(7+8)= 5+6+7+8=26
EN EFECTO: AL AÑADIR LA SUMA 7+8 AL SUMANDO 6 DE LA
PRIMERA, ESTA SUMA QUEDA AUMENTADA EN 7 +8 UNIDADES POR
LA MISMA RAZÓN DEL CASO ANTERIOR.

19. Operaciones
indicadas de suma
y resta …
Suma de un numero y una diferencia indicada
PARA SUMAR UN NUMERO CON UNA DIFERENCIA INDICADA, SE
SUMA EL NUMERO CON EL MINUENDO Y DE ESTA SUMA SE RESTA
EL SUSTRAENDO.
SEA LA OPERACIÓN (7-5)+4, DECIMOS QUE:
(7-5)+4=(7+4)-5=11-5=6
EN EFECTO: AL SUMAR EL NUMERO 4 AL MINUENDO, LA
DIFERENCIA 7-5 QUEDA AUMENTADA EN 4 PORQUE HEMOS VISTO
QUE SI EL MINUENDO SE AUMENTA EN UN NUMERO
CUALQUIERA, LA DIFERENCIA QUE AUMENTADA EN ESE NUMERO.

20. Operaciones
indicadas de suma
y resta …
Suma de diferencias indicadas
PARA SUMAR DOS O MAS DIFERENCIAS INDICADAS, SE SUMAN LOS MINUENDOS
Y DE ESTA SUMA SE RESTA LA SUMA DE LOS SUSTRAENDOS.
SEA LA OPERACIÓN (8-5)+(6-4), DECIMOS QUE:
(8-5)+(6-4)= (8+6)-(5+4) = 14-9=5
EN EFECTO: AL SUMAR EL MINUENDO 8 EL MINUENDO6, LA DIFERENCIA
(8-5) QUE DA AUMENTADA EN 8 UNIDADES, PERO AL RESTAR EL SUSTRAENDO 6
QUEDA DISMINUIDA EN 6 UNIDADES, LUEGO SI LA SUMA (4+5) AUMENTA 8 Y
DISMINUYE 6 AUMENTA 2 QUE ES LA DIFERENCIA
8-6

21. Operaciones
indicadas de suma
Resta .. y resta …
Resta de un numero y una suma indicada
PARA RESTAR DE UN NUMERO UNA SUMA INDICADA, SE RESTAN DEL
NUMERO, UNO A UNO, TODOS LOS SUMANDOS DE LA SUMA.
SEA LA OPERACIÓN 25-(2+3+4)= 25-2-3-4= 16
EN EFECTO: SI 25 SE DISMINUYE PRIMERO EN 2, DESPUÉS EN 3 Y LUEGO EN
4, QUEDA DISMINUIDO EN 9 UNIDADES QUE ES LA SUMA 2+3+4.

22. Operaciones
indicadas de suma
y resta …
Resta de una suma indicada y un numero
PARA RESTA DE UNA SUMA INDICADA Y UN NUMERO, SE RESTA EL
NUMERO DE CUALQUIER SUMANDO DE LA SUMA.
SEA LA OPERACIÓN (4+5+6)-3, PROBAR QUE:
(4+5+6)-3=(4-3)+5+6=12
EN EFECTO: AL RESTAR EL 3 DE UNO DE LOS SUMANDOS DE LA
SUMA, ESTA QUEDA DISMINUIDA EN 3 UNIDADES.

23. Operaciones
indicadas de suma
Resta de un numero y una diferencia indicada
y resta …
PARA RESTAR DE UN NUMERO UNA DIFERENCIA INDICADA, SE
SUMA EL SUSTRAENDO CON EL NUMERO Y DE ESTA SUMA SE RESTA
EL MINUENDO
SEA L A OPERACIÓN 50-(8-5), QUE DECIMOS QUE :
50-(8-5)= (50+5)-8=47
EN EFECTO: SABEMOS QUE SI AL MINUENDO Y AL SUSTRAENDO DE
UNA DIFERENCIA SE SUM A UN MISMO NUMERO, LA DIFERENCIA
NO VARIA. AÑADIENDO 5 AL MINUENDO Y AL SUSTRAENDO DE LA
DIFERENCIA 50-(8-5), TENEMOS.
50-(8-5)= (50+5)-(8-5+5) = (50+5)-8
POR QUE SI AL 8 RESTAMOS 5 Y LE SUMAMOS 5 QUEDA 8

24. Operaciones
indicadas de suma
y resta …
Resta de una diferencia indicada y un numero
PARA RESTAR DE UNA DIFERENCIA INDICADA UN NUMERO, SE
RESTA DEL MINUENDO LA SUMA DEL SUSTRAENDO Y EL NUMERO.
SEA LA OPERACIÓN (15-7) -6, DECIMOS QUE:
(15-7) -6=15-(7+6)=15-13= 2
EN EFECTO: AL SUMAR 6 CON EL SUSTRAENDO 7, LA DIFERENCIA 15-
7 QUEDA DISMINUIDA EN 6 UNIDADES PORQUE SI AL SUSTRAENDO
SE SUMA UN NUMERO CUALQUIERA. LA DIFERENCIA QUEDA
DISMINUIDA EN ESTE NUMERO.

25. Operaciones
indicadas de suma
y resta …
Resta de dos sumas indicadas
PARA RESTAR DOS SUMAS INDICADAS SE RESTAN DE LA PRIMERA
SUMA, UNO A UNO, TODOS LOS SUMANDOS DE LA SEGUNDA SUMA.
SEA LA OPERACIÓN (4+5)-82+3)= 4+5-2-3=4
EN EFECTO: SI DE LA SUMA (4+5) RESTAMOS PRIMERO 2 Y DESPUÉS
3, ESTA SUMA QUEDA DISMINUIDA EN 5 UNIDADES QUE ES LA SUMA
2+3.

26. Operaciones
indicadas de suma
Resta de dos diferencias indicadas
y resta …
PARA RESTAR DOS DIFERENCIAS INDICADAS, SE SUMA EL MINUENDO DE
LA PRIMERA CON EL SUSTRAENDO DE LA SEGUNDA Y DE ESTA SUMA SE
RESTA DEL SUSTRAENDO DE LA PRIMERA CON EL MINUENDO DE LA
SEGUNDA.
SEA LA OPERACIÓN (8-1) –(5-3)=(8+3)-(5+1)= 11 -6=5
EN EFECTO: AL SUMAR EL SUSTRAENDO 3 CON EL MINUENDO 8 LA
DIFERENCIA (8-1) QUEDA AUMENTADA EN 3 UNIDADES, PERO AL SUMAR
EL MINUENDO 5 CON EL SUSTRAENDO 1 LA DIFERENCIA (8-1) QUEDA
AUMENTADA EN 3 UNIDADES, PERO AL SUMAR EL MINUENDO 5 CON EL
SUSTRAENDO 1 LA DIFERENCIA (8-1) QUEDA DISMINUIDA EN 5 UNIDADES;
LUEGO SI (8-1) AUMENTA 3 DISMINUYE 5, EN DEFINITIVA DISMINUYE
2, QUE ES LA DIFERENCIA 5-3

27. Operaciones
indicadas de suma
y resta …
Resta de una suma y una diferencia
indicada.
PARA RESTAR DE UNA SUMA UNA DIFERENCIA INDICA, SE SUMA EL
SUSTRAENDO CON LA SUMA INDICADA U DE ESTA SUMA SE RESTA
EL MINUENDO.
SEA LA OPERACIÓN (8+4)-(3-2), PROBAR QUE:
(8+4)-(3-2)=(8+4+2)-3= 14-3=11
EN EFECTO: AL SUMAR EL SUSTRAENDO 2 CON LA SUMA (8+4) ESTA
SUMA QUEDA AUMENTADA EN 2 UNIDADES, PERO AL RESTAR EL
MINUENDO 3 DISMINUYE 3 UNIDADES, LUEGO SI AUMENTA 2
DISMINUYE 3 , DISMINUYE 1 UNIDAD QUE ES LA DIFERENCIA (3-2)

28. Operaciones
indicadas de suma
y resta …
Casos particulares.
La suma de dos números mas su diferencia en igual al
doble del mayor.
SEAN LOS NÚMEROS 8Y 5, DECIMOS QUE :
(8+5 )+(8-5)=2X8= 16
EN EFECTO : SABEMOS QUE PARA SUMAR UNA SUMA CON UNA
DIFERENCIA, SE SUMA EL MINUENDO DE LA DIFERENCIA CON UNO DE
LOS SUMANDOS DE LA SUMA Y DE ESTA SUMA SE RESTA EL
SUSTRAENDO, LUEGO :

29. Operaciones
indicadas de suma
La suma de dos números menos … diferencia es
y resta su
igual al doble del menor
SEAN LOS NÚMEROS 8 Y 5, DECIMOS QUE:
(8+5)+(8-5)= 2X5=10
EN EFECTO: SABEMOS QUE PARA RESTAR DE UNA SUMA UNA
DIFERENCIA SE SUMA EL SUSTRAENDO CON LA SUMA Y DE ESTA
SUMA SE RESTA EL MINUENDO, LUEGO :
(8+5)-(8-5)=8+5-5+8= 5+5+8-8= 5+5= 2X5

30. TRABAJO:
COMPLEMENTO ARITMÉTICO
PROFESOR:
JOSÉ CALIXTO SALAS GONZÁLEZ
SEMESTRE: ESPECIALIDAD:
3° MATEMÁTICAS

31. COMPLEMENTO ARITMÉTICO
El complemento aritmético de un número es la
diferencia entre dicho número y una unidad de un
orden superior a su cifra de mayor a menor.
1) El complemento aritmético de 98
es 100-98 = 2
2) El complemento aritmético de 356
es 1000-356 = 644
3) El complemento aritmético de 1,250
es 10,000-1,250 = 8,750
4) El complemento aritmético de 14,200
es 100,000-14,200 = 85,800

32. REGLA PRÁCTICA PARA HALLAR EL
COMPLEMENTO DE UN NÚMERO
Se resta de 9 todas las cifras del
número, empezando por la
izquierda, menos la última cifra
significativa, que se resta de 10. si el
número termina en ceros, a la derecha
de la última resta se escriben estos ceros.

33. EJEMPLOS:
1) Hallar el complemento aritmético de 346.
diremos: de 3 a 9 = 6; de 4 a 9 = 5; de 6 a 10 = 4,
luego el complemento aritmético de 346 es 654.
2) Hallar el complemento aritmético de 578, 900.
diremos: de 5 a 9 = 4; de 7 a 9 = 2; de 8 a 9 = 1; de
9 a 10 = 1,
luego el complemento aritmético es 421,100

34. APLICACIÓN DEL COMPLEMENTO
ARITMÉTICO PARA EFECTUAR LA RESTA
Para efectuar la resta por medio del
complemento aritmético se suma el minuendo
con el complemento aritmético del
sustraendo, poniéndole a este delante una
unidad son signo menos, que se tendrá al
efectuar la suma.
1) Efectuar 1,034 – 615 por medio del
complemento aritmético.

35. Es el complemento aritmético con una unidad
con signo menos adelante, y tendremos:
1, 034
+ 1, 385
0, 419
La diferencia entre 1,034 y 615 es 419, que se
puede comprobar efectuando la resta:
1, 034
- 615

36. APLICACIÓN DEL COMPLEMENTO ARITMÉTICO
PARA EFECTUAR VARIAS SUMAS Y RESTAS
COMBINADAS
Para efectuar sumas y restas combinadas por
medio del complemento aritmético se suman
todos los sumandos con los complementos
aritméticos de los sustraendos , poniendo
delante de cada complemento una unidad con
signo menos, que se tomara en cuenta al
efectuar la suma.

37. EJEMPLOS:
1) Efectuar por los componentes 56 – 41 + 83 – 12.
_56
Comp.. Aritmético de 41… 159
+ _83
Comp.. Aritmético de 12… 188
86

38. TRABAJO:
MULTIPLICACIÓN
PROFESOR:
JOSÉ CALIXTO SALAS GONZÁLEZ
SEMESTRE: ESPECIALIDAD:
3° MATEMÁTICAS

39. Es una operación de composición que tiene por
objeto, dados números llamados multiplicando y
multiplicador, hallar un numero llamado producto
que sea respecto del multiplicando lo que el
multiplicador es respecto de la unidad.

40. El producto de dos números se indica con el signo X o
con punto colocado entre los factores, que es el
nombre que se le da al multiplicando y multiplicador.
Así, el producto de 6 por 5 se indica 6 x 5 o 6 · 5

41. 1) Si el multiplicador es cero, el producto es cero.
2) Si el multiplicador es 1, el producto es igual al
multiplicando.
3) Si el multiplicador es >1, el producto es > el
multiplicando.
4) Si el multiplicador es < 1, el producto es < el
multiplicando.

42. Cuando el multiplicador es un numero
natural, la multiplicación es una suma
abreviada que consta de tantos sumandos
iguales al multiplicando como unidades tenga
el multiplicador
4x3= 4+4+4+4=12

43. Para multiplicar un entero por la unidad
seguida de ceros se añaden al entero tantos
ceros como ceros acompañen a la unidad.
54 x 100 = 5400, por que el valor relativo de cada
cifra se ha hecho 100 veces mayor

44. Se multiplican los números como si no tuvieran ceros y
a la derecha de este producto se añaden tantos ceros
como haya en el multiplicando y multiplicador.
4300 x 2500 = 107 500 000

45. En el producto hay siempre tantas cifras como
haya en el multiplicando y multiplicador
juntos o una menos.
345 x 23 > 345 x 10, y como este
Así, el producto ultimo producto 345 x 10 = 3450
345 x 23 ha de tiene cuatro cifras, el producto
tener cuatro 345 x 23, que es mayor que el, no
cifras o cinco. puede tener menos de cuatro
cifras.
7935

46. Representar gráficamente 3x2
2
3 2
3
Se construye un rectángulo cuya base sea el segmento que
representa el 3 y cuya altura sea el segmento que
representa el 2. El rectángulo ABCD que consta de dos filas
horizontales de 3 cuadrados cada una es la representación
grafica del producto 3 x 2 = 6

47. Para hallar el producto de mas de dos números como
2x3x4x5
1. Se halla el producto de dos de ellos.
2. Luego se multiplica este producto por el tercero.
3. Luego este segundo producto por el factor siguiente y
así hasta el ultimo factor.
2x3=6
Así, en este 6 x 4 = 24
caso, tendremos:
24 x 5 = 120

48. Pueden realizarse de tres modos:
1. Cambiando el
orden de los 3. Por la prueba
factores, lo cual del 9
debe darnos el 2. Dividiendo el
mismo producto. producto entre
uno de los
factores, lo cual
debe darnos el
otro factor.

49. Enunciarse de tres modos:
3. Productos de dos
1. El producto de 2. Los productos
igualdades.
dos números de números
Multiplicando
tiene un valor respectivamente
miembro a miembro
único o siempre iguales son
varias igualdades
igual. iguales.
resulta otra
igualdad.
5 sillas x 2 = 10 sillas
5 días x 2 = 10 días
a=b
5 x 2 = 10 c=d
ac = bd

50. El orden de los factores no altera el producto
1. Que se trate de 2. Que se trate de
dos factores mas de dos factores
Vamos a demostrar que 6
Sea el producto 5 x 4 x 3 x 2
x 4 = 4 x 6.
Se puede considerar
6x 4 = 6 + 6+ 6+ 6+ 6= 24 descompuesto en dos factores:
4 x 6= 4+ 4+ 4+ 4+ 4 +4= 24 5.4y3.2

51. El producto de varios números no varia
sustituyendo dos o mas factores por su
producto
2 x 3 x 4 x 5 = 120 En general:
(2 x 3) x 4 x 5 = 120
6 abcd = (ab)cd = a(bcd)
(2 x 3) x (4 x 5) = 120
6 20

52. El producto
de varios
números no Sea el producto 8 x 5;
puesto que 8 = 4 x
varia
2, tendremos:
descomponie
ndo uno o 8x5=4x2x5
mas factores
en dos o mas
factores

53. TRABAJO:
OPERACIONES INDICADAS DE MULTIPLICACIÓN
PROFESOR:
JOSÉ CALIXTO SALAS GONZÁLEZ
SEMESTRE: ESPECIALIDAD:
3° MATEMÁTICAS

54. OPERACIONES INDICADAS DE MULTIPLICACION EN QUE
NO HAY SIGNOS DE AGRUPACION.
• Para comenzar, deben efectuarse en este
orden: primero, los productos indicados y
luego las sumas o restas.
• Ejemplo: efectuar, 5+3x4-2x7
• Efectuamos primero los productos 3x4=12 y
2x=14 y tendremos:
• 5+3x4-2x7 =5+12-14= 3.

55. PERACIONES INDICADAS DE MULTIPLICACION
EN QUE HAY SIGNOS DE AGRUPACION.
• PRIMERO: Las operaciones encerradas en los
paréntesis y luego las operaciones que queden
indicadas.
• Ejemplo: (5+3)2+3(6-1).
• En la practica, se suele suprimir el signo x entre un
numero y un paréntesis o entre dos paréntesis.
• A si pues, en este ejemplo, (5+3) 2 equivale a (5+3) x 2
y 3(6-1) equivale a 3 x (6-1).
• Entonces efectuamos primero los paréntesis, (5+3) = 8
y (6-1)= 5, y tendremos: (5+3) 2 + 3(6-1)= 8 x 2 + 3 x 5=
16 + 15= 31.

56. LEY DISTRIBUTIVA DE LA MULTIPLICACION.
PRODUCTO DE UNA SUMA POR UN NUMERO.
• Para multiplicar una suma indicada por un
numero se multiplica cada sumando por este
numero y se suman los productos parciales.
• Ejemplo: (5+4)2.
• Decimos que, (5+4)2= 5x2+4x2=10+8=18
• Entonces: (5+4)2 = (5+4) + (5+4) = 5+4+5+4=
5+5+4+4= (5+5) + (4+4) = 5x2+4x2.

57. Producto de una resta por un numero.
• Para multiplicar una resta indicada por un numero se
multiplican el minuendo y el sustraendo por este
numero y se restan los productos parciales.
• Ejemplo: (8-5) 3.
• Asi que decimos:
(8 – 5) 3 = 8 x 3 – 5 x 3 =24 – 15 = 9
Entonces multiplicar (8 – 5) 3 equivale a tomar (8 – 5)
como sumando tres veces, o sea:
(8 – 5) 3 = (8 – 5)+ (8 – 5) + (8 – 5)
o también realizar lo siguiente: = (8+8+8) – (5+5+5) = 8 x
3 – 5 x 3.

58. Suma algebraica.
• Una expresión como 7 – 2 + 9 – 3 que
contiene varios signos + o – es una suma
algebraica. En esta suma algebraica, 7, 2, 9 y 3
son los términos de la suma. Los términos que
van precedidos del signo + o que no llevan
signo delante son positivos. Asi que en este
caso, -2 y -3 son negativos.
• En la suma algebraica a + b – c – d + e, los
términos positivos son a,b y e, y los
negativos, -c y –d.

59. Productos de una suma algebraica por
un numero
• Para multiplicar una suma por un numero se
multiplica un termino de la suma por dicho
numero, poniendo delante de cada producto
parcial el signo + si el termino que se multiplica
es positivo y el signo – si es negativo.
• Ejemplo: (8 – 2 + 6 – 3) 5.
• Asi que decimos:
• (8-2+6-3)5 = 8 x 5 – 2 x 5 + 6 x 5 – 3 x 5
• = 40 – 10 + 30 – 15 =45
• En general: (a – b + c –d )n = an – bn + cn – dn.

60. Factor común
• En la suma algebraica x 5 + 3 x 2 – 4 x 2 los
términos son los productos 2x5, 3x2 y 4x2. en
cada uno de estos productos aparece el factor
2; 2 es un factor común.
• Igualmente en la suma algebraica 9 x 3 – 3 x 5
-3 x 2 +8 x 3 el 3 es un factor común; en la
suma ab + bc – bd el factor común es b; en la
suma 5 ay + 5ax – 5an el factor común es 5 a.

61. Producto de sumas y diferencias.
Producto de 2 sumas.
• Para multiplicar dos sumas indicadas se
multiplican todos los términos de la primera por
cada uno de los términos de la segunda y se
suman los productos parciales.
• Entonteces efectuamos (6+5)(3+2) y decimos
que: (6+5)(3+2)=6x3+5x3+6x2+5x2
=18+15+12+10 =55.
• En efecto: el producto (6+5) (3+2) se compondrá
de tres veces (6+5) mas dos veces (6+5), luego:
(6+5)(3+2)=(6+5)3+(6+5)2 =6x3+5x3+6x2+5x2.

62. Producto de un producto indicado por
un numero.
• Para multiplicar un producto indicado por un
numero se multiplica uno de los factores del
producto por dicho numero.
• Vamos a multiplicar el producto 4 x 5 por 6.
• Decimos que basta multiplicar uno solo de los
factores, bien el 4 o el 5, por el multiplicador
6.
• Multiplicando el factor 5, tenemos:
• (4x5)6 = 4(5x6)=4(30)=120.

63. Producto de dos productos indicados.
• Para multiplicar dos productos indicados se
forma un solo producto con todos los factores.
• Vamos a multiplicar el producto 2x3 por el
producto 4x5x6. Decimos que:
• (2x3)(4x5x6)=2 x 3 x 4 x 5 x 6 = 720.
• Entonces al multiplicar el factor 3 del producto
2x3 queda multiplicado por el producto
4x5x6, según el caso anterior.

64. TRABAJO:
DIVISIÓN
PROFESOR:
JOSÉ CALIXTO SALAS GONZÁLEZ
SEMESTRE: ESPECIALIDAD:
3° MATEMÁTICAS

66. INVERSA DE LA MULTIPLICACIÓN
SU ODJETO DADO EL PRODUCTO DE 2 FACTOREDS
(DIVIDENFO Y UNO DE LOS FACTORES
(DIVISOR), HALLAR EL OTRO FACTOR (COCIENTE)

68. • DIVIDIR UN NÚMERO (DIVIDENDO) ENTRE OTRO (
DIVISOR) ES HALLAR UN NÚMERO (COCIENTE) QUE
MULTIPLICADO POR EL DIVISOR DE EL DIVIDENDO.
• EJEMPLO 20/4 ES ALLAR EL NÚMERO QUE
MULTIPLICADO POR 4 DE 20
• 4x5=20

69. • Del propio modo: 8 4 =2 por que
2x4 =8
15 5
3

71. TODO NÚMERO QUE DIVIDE A OTROS
VARIOS, DIVIDE A SU SUMA SEA EL NÚMERO 5
, QUE DIVIDE AL 10, 15, 20=45, O SEA QUE
10+25+20 ES M. 5
EN EFECTO: 10=5x2; 15= 5x3; 20= 5x4

72. • Sacando el valor común 5 en el segundo
miembro de la ultima
igualdad, tenemos:
10+15+20= 5 (2+3+4) o sea 10+15+20=
5x9
10+15+20= 45, contiene al 5, 9 veces y 5
divide a la suma 10+5+20

73. • Todo número que no divide a otro
vario divide a su suma, si la suma de
los residuos que resultan de dividir
estos entre el número que no los
divide, es divisible entre este número.

74. • El 7, no divide a 15, 37 • Vamos a probar que
y 46. 7 divide a
• El residuo de 15 7 = 1 15+37+46=98
• 37 7= 2 15= 7x2+1
• 46 7 = 4 y la suma 37= 7x5+2
de estos es 7 46= 7x6+4