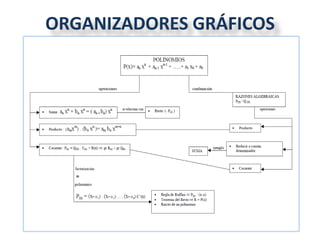
Este documento trata sobre las operaciones con polinomios. Define polinomios como expresiones algebraicas formadas por la suma de términos, donde cada término está formado por un coeficiente y variables con exponentes. Explica cómo sumar polinomios colocándolos unos debajo de otros para alinear términos semejantes, y cómo reducir términos semejantes sumando sus coeficientes. También cubre la notación, organizadores gráficos y propiedades básicas de los polinomios.

1. Definición
Notación
Organizadores gráficos
Propiedades
Reglas
Operaciones
Aplicaciones
Ejercicios
ELABORADO POR : Aaron Bravo V.

2. OPERACIONES CON POLINOMIOS
En la práctica para sumar dos o más polinomios suelen colocarse unos debajo de los
otros, de tal modo que los términos semejantes queden en columna, para facilitar la
reducción de éstos, separados unos de otros con sus respectivos signos.
Dados que los polinomios , de la forma general: o de forma compacta mediante el
Sumatorio de los términos del polinomio:
Podemos definir como operaciones con polinomios, las operaciones aritméticas o
algebraicas, que partiendo de uno o más de esos polinomios nos da unos valores u
otro polinomio, según la operación de que se trate.
Así como la aritmética surgió de la necesidad que tenían los pueblos primitivos de
medir el tiempo y de contar sus posesiones, el origen del álgebra es muy posterior
puesto que debieron de transcurrir muchos siglos para que el hombre llegara al
concepto abstracto de número que es el fundamento del álgebra. El gran desarrollo
experimentado por el álgebra se debió sobre todo a los matemáticos árabes y, muy en
particular, a Al-Hwarizmi (Siglo IX d.C.), que sentó las bases del álgebra tal como la
conocemos hoy en día.
El álgebra es la parte de las matemáticas que tienen por objeto generalizar todas las
cuestiones que se pueden proponer sobre las cantidades.
El concepto algebraico de cantidad es mucho más amplio que el aritmético, puesto
que mientras en aritmética las cantidades se representan mediante números que
expresan valores determinados, en álgebra las cantidades se representan mediante
letras que pueden representar cualquier valor que se les asigne.

3. NOTACIÓN

5. • 100 = 1
• 101 = 10
• 102 = 100
• 103 = 1 000
• 104 = 10 000
• 105 = 100 000
• 106 = 1 000 000
• 107 = 10 000 000
• 108 = 100 000 000
• 109 = 1 000 000 000
• 1010 = 10 000 000 000
• 1020 = 100 000 000 000 000 000 000
• 1030 = 1 000 000 000 000 000 000 000 000 000 000

6. ORGANIZADORES GRÁFICOS

7. SIGNOS ALGEBRAICOS DE OPERACIÓN, DE
RELACIÓN Y DE AGRUPACIÓN

8. SIGNOS DE RELACIÓN

10. TÉRMINO ALGEBRAICO Y SUS PARTES
Se llama término a toda expresión algebraica cuyas partes no están separadas por
los signos + o -. Así, por ejemplo xy2 es un término algebraico.
En todo término algebraico pueden distinguirse cuatro elementos: el signo, el
coeficiente, la parte literal y el grado.

11. Signo
Los términos que van precedidos del signo + se llaman términos positivos, en tanto
los términos que van precedidos del signo – se llaman términos negativos. Pero, el
signo + se acostumbra omitir delante de los términos positivos; así pues,
cuando un término no va precedido de ningún signo se sobreentiende de que es
positivo.
Coeficiente
Se llama coeficiente al número o letra que se le coloca delante de una cantidad para
multiplicarla. El coeficiente indica el número de veces que dicha cantidad debe
tomarse como sumando. En el caso de que una cantidad no vaya precedida de un
coeficiente numérico se sobreentiende que el coeficiente es la unidad.
Parte literal
La parte literal está formada por las letras que haya en el término.
Grado
El grado de un término con respecto a una letra es el exponente de dicha letra. Así,
por ejemplo el término x3y2z, es de tercer grado con respecto a x, de segundo grado
con respecto a y y de primer grado con respecto a x.

12. CLASIFICACIÓN DE LOS TÉRMINOS
ALGEBRAICOS; SEMEJANTES Ó NO SEMEJANTES
Los términos que tienen las mismas variables con los
mismos exponentes se llaman términos semejantes como
por ejemplo:
y son términos semejantes.
y son términos semejantes.
y no son términos semejantes.
y no son términos semejantes.

13. REDUCCIÓN DE TÉRMINOS SEMEJANTES
Se llama reducción de términos semejantes a la operación que consiste en
reemplazar varios términos semejantes por uno solo. En la reducción de
términos semejantes pueden presentarse los tres casos siguientes:
a) Para reducir términos semejantes que tengan igual signo se suman los
coeficientes anteponiendo a la suma el mismo signo que tienen todos los
términos y a continuación se escribe la parte literal.
Ejemplo:
Reducir las siguientes expresiones