Este documento describe medidas de forma como la simetría, asimetría, apuntamiento y achatamiento de distribuciones de datos. Explica cómo calcular el coeficiente de asimetría de Pearson y Fisher para determinar si una distribución es simétrica o asimétrica, y el coeficiente de curtosis de Fisher para determinar si una distribución es mesocúrtica, leptocúrtica o platicúrtica. También presenta ejemplos prácticos de cálculos de estos coeficientes.

1. Universidad de Los Andes
Facultad de Medicina
Cátedra de Bioestadística
MEDIDAS DE FORMA
Prof. Joan Fernando Chipia Lobo
@JoanFChipiaL

2. MEDIDAS DE FORMA
Es la apariencia externa de la distribución de
frecuencias o de una colección de datos
cuantitativos y viene dada representada por el
aspecto gráfico.
Dentro de la forma se incluye simetría o
asimetría de la curva y el grado de
apuntamiento o achatamiento de la curva.
Son medidas relativas, es decir son cocientes
o razones y no vienen expresadas en ninguna
unidad de medida

3. Ejemplos de curvas simétricas
Distribución simétrica y unimodal
Distribución uniforme
Distribución con forma de U
Una distribución es simétrica cuando la curva que la
representa es exactamente igual a ambos lados del
punto de referencia.

4. Distribución asimétrica
negativa
Una distribución unimodal es
asimétrica negativa si los
datos se concentran hacia los
valores altos de la variable (en
el lado derecho de la gráfica)
Distribución
asimétrica positiva
Una distribución unimodal
es asimétrica positiva si los
datos se concentran hacia
los valores bajos (o
pequeños) de la variable (en
el lado izquierdo de la
gráfica)
MoMdx 
MoMdx 
EJEMPLOS

5. COEFICIENTE DE ASIMETRÍA DE PEARSON
Este coeficiente está basado entre la relación existente entre la
media y la mediana
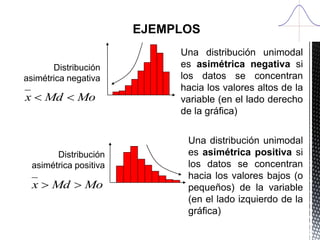
1. Si el valor del coeficiente de asimetría es mayor que cero
entonces la distribución presenta una asimetría positiva.
2. Si el valor del coeficiente de asimetría es menor que cero
entonces la distribución presenta una asimetría negativa.
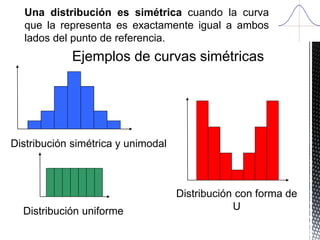
3. Si el valor del coeficiente de asimetría es igual a cero entonces
la distribución es simétrica.
4. El coeficiente varía entre [-3,3] aunque valores fuera de [-1,1]
se consideran excepcionales

6. EJEMPLO
Hallar la asimetría del siguiente problema
Problema: Los estudios de Dosman et al. Permiten concluir
que la aspiración de aire frío incrementa la reactividad
bronquial al inhalar histamina en pacientes asmáticos. Se
estudiaron 20 pacientes asmáticos con edades entre 19 y 33
años cumplidos. Los valores de línea de base (en litros por
minuto) del volumen respiratorio forzado de los individuos de la
muestra son los siguientes:
3.94 1.50 2.06 2.36 3.74 3.43 3.78 2.50
2.88 2.99
3.78 1.99 3.41 2.36 3.76 3.55 3.33 2.77
3.03 3.44
Tomado de Daniel, W. (2010). Bioestadística: Base para el
análisis de las ciencias de la salud (4a. Ed.). México: Limusa
Wiley.

7. SOLUCIÓN:
𝑥 = 3,03 𝑙𝑖𝑡𝑟𝑜𝑠 𝑝𝑜𝑟 𝑚𝑖𝑛𝑢𝑡𝑜
𝑀𝑑 = 3,18 𝑙𝑖𝑡𝑟𝑜𝑠 𝑝𝑜𝑟 𝑚𝑖𝑛𝑢𝑡𝑜
𝑆 = 0,7055 𝑙𝑖𝑡𝑟𝑜𝑠 𝑝𝑜𝑟 𝑚𝑖𝑛𝑢𝑡𝑜
𝐴𝑆𝑃 =
3(𝑥 − 𝑀𝑑)
𝑆
=
3 3,03 − 3,18 𝑙𝑖𝑡𝑟𝑜𝑠 𝑝𝑜𝑟 𝑚𝑖𝑛𝑢𝑡𝑜
0,7055 𝑙𝑖𝑡𝑟𝑜𝑠 𝑝𝑜𝑟 𝑚𝑖𝑛𝑢𝑡𝑜
= −0,6378
Interpretación: la distribución del volumen respiratorio forzado de
los individuos de la muestra es asimétrica negativa, con un valor
aproximado de -0,64.

8. COEFICIENTE DE ASIMETRÍA DE FISHER
Datos no agrupados Datos agrupados
A =
(xi − x)n
i=1
3
ni
n
s3
=
m3
s3
A =
(xm − x)n
i=1
3
ni
n
s3
=
m3
s3
Otra manera de hallar la Asimetría es con el:

9. COEFICIENTE DE CURTOSIS DE FISHER
Estas medidas indican el grado de apuntamiento o
achatamiento del gráfico correspondiente a una distribución
de frecuencias. La medición del apuntamiento de un gráfico
se hace tomando como referencia la curva normal (es decir
una curva unimodal simétrica en forma de campana).
Datos no agrupados Datos agrupados
Cu =
(xi − x)n
i=1
4
ni
n
s4
=
m4
s4
Cu =
(xm − x)n
i=1
4
ni
n
s4
=
m4
s4

10. A la curva normal se le llama mesocúrtica, si es más
puntiaguda se le llama leptocúrtica y si es más achatada
platicúrtica.
Los indicadores de curtosis, miden el nivel de
concentración de datos en la región central.

11. Distribución
Leptocúrtica
Distribución
Platicúrtica
Distribución
Mesocúrtica
Si el valor del coeficiente de
curtosis es mayor que tres
entonces la distribución es
leptocúrtica.
Si el valor del coeficiente de asimetría
es menor que tres entonces la
distribución es platicúrtica.
Si el valor del coeficiente de
asimetría es igual a tres entonces
la distribución es mesocúrtica.
CRITERIOS PARA INTERPRETAR EL COEFICIENTE DE
CURTOSIS.

12. Se ha medido el aclaramiento de creatinina en pacientes
tratados con Captopril tras la suspensión del tratamiento
con diálisis, resultando la siguiente tabla:
Creatinina (mg/dl) 5,7 5,2 4,8 4,5 4,2
𝑥𝑖 𝑥𝑖 − 𝑥 (𝑥𝑖 − 𝑥)4
5,7 5,7- 4,9= 0,8 0,4096
5,2 5,2 – 4,9= 0,3 0,0081
4,8 4,8 – 4,9= -0,1 0,0001
4,6 4,6 – 4,9= -0,3 0,0081
4,2 4,2 – 4,9= -0,7 0,2401
Suma 0,666
𝑔2 =
𝑚4
𝑠4
=
0,666
(0,264)4
= 137, 09
Interpretación: La creatinina presenta una distribución
leptocurtica.

13. PRÁCTICA
Problema: El objetivo de un estudio fue analizar
ciertos parámetros farmacocinéticos básicos en
mujeres tratadas con anticonceptivos trifásicos de
ingestión oral. Los pesos (Kg.) de las 10 mujeres que
participaron en el estudio son:
62 53 57 55 69 64 60 59 60 60
Fuente: datos supuestos.
Halle e interprete la asimetría y curtosis de la serie de
datos.

14. “Quien hace que las cosas difíciles
parezcan fáciles es el educador.”
Emerson
FINALMENTE, LOS INVITO A LA PÁGINA WEB DE
BIOESTADÍSTICA:
URL http://www.webdelprofesor.ula.ve/ciencias/joanfchipia/

15. REFERENCIA
Armas, J. (1988). Estadística Sencilla: Descriptiva. Mérida:
Consejo de Publicaciones de la Universidad de Los Andes.