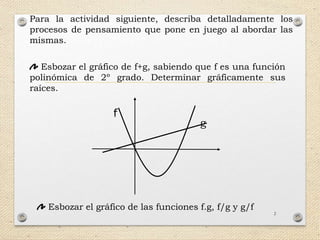
El documento describe la evolución histórica de las representaciones de las funciones a través de diferentes etapas: tablas, gráficos, expresiones algebraicas y series infinitas. Explica que cada representación enfatiza aspectos diferentes del concepto de función y que la comprensión del concepto requiere la capacidad de convertir entre representaciones. Finalmente, destaca la importancia de trabajar con múltiples representaciones para favorecer la construcción del concepto.

1. 1
Registros de
representación semiótica:
las funciones
Mario Dalcín – Mónica Olave – Yacir Testa
Instituto de Profesores Artigas

2. Para la actividad siguiente, describa detalladamente los
procesos de pensamiento que pone en juego al abordar las
mismas.
Esbozar el gráfico de f+g, sabiendo que f es una función
polinómica de 2º grado. Determinar gráficamente sus
raíces.
2
g
f
Esbozar el gráfico de las funciones f.g, f/g y g/f

3. 3
¿Qué nos dice la historia?
1ª Etapa: representación tabular.
• 2000 a.C. Babilonios: tablas de cuadrados, cubos,
astronómicas.
• Siglo V a.C. Pitagóricos: las longitudes y los tonos de
las notas emitidas por cuerdas de la misma especie, al
ser pulsada bajo tensiones iguales.
• Época alejandrina: trigonometría de las cuerdas
correspondientes a una circunferencia de radio fijo.
• Siglo XI. Mayas: Códice de Dresde donde se encuentra
material astronómico - astrológico en dos tablas: de
eclipses y de Venus.

4. 4
2ª Etapa: representación gráfica.
• Nicolás de Oresme (1323-1382) que propone
en su Treatise, “representar a las cosas que
varían mediante un dibujo, señalando que ...
todo lo que varía, se sepa medir o no, lo
podemos imaginar como una cantidad
continua representada como un segmento
rectilíneo”. (Citado en Youschkevitech, 1997).

5. 5
3ª Etapa: representación algebraica
• En 1591 Vieta (1540-1603) introduce los símbolos para
representar cantidades conocidas y desconocidas
• Esto influye en forma determinante en los trabajos de
Descartes (1596-1650) y Fermat (1601-1655).
• Se introduce a las funciones en forma de ecuación lo
que representa el nacimiento del “marco algebraico” en el
cual el uso de las expresiones analíticas permite efectuar
operaciones con reglas específicamente definidas.
• Descartes por primera vez, y en forma perfectamente
clara, sostiene que una ecuación en x e y es un medio
para introducir una dependencia entre cantidades
variables, que permite el cálculo de los valores de una de
ellas que corresponden a valores dados de la otra.

6. 6
4ª Etapa: representación analítica
(serie infinita de potencias de la variable).
En la etapa anterior, la gama de las funciones que se
expresaban analíticamente se limitaban a las algebraicas , y
Descartes incluso excluyó de su geometría a todas las curvas
mecánicas porque, a su parecer no se prestaban a su método de
análisis.
En esta etapa se afianza la aceptación de los procesos infinitos
en matemáticas; esta aceptación es llevada al universo de las
dependencias funcionales concebibles, pues se trabaja en
desarrollar todas las funciones conocidas en la época en series
de potencias infinitas (para que estas sean susceptibles al
análisis).
J. Bernoulli y L. Euler, definen entonces el concepto de
función, diciendo que se trata de una expresión analítica,
cuya forma más general es una serie de potencias, definición
que fue aceptada por la mayoría de los matemáticos de esa
época.

7. 5ª Etapa: Simbolización y definición general
• La definición de Dirichlet – Bourbaki: la
relación entre pares de elementos de dos
conjuntos A y B, tal que a cada elemento x 
A se le asigna un elemento y, y sólo uno, tal
que y  B, según alguna regla definida.
7

8. ABCD rectángulo donde AB = 6 cm y BC = 9 cm.
Se consideran los puntos M, N, O, P,
pertenecientes a los segmentos AB, BC, CD, DA
respectivamente, de modo que AM = BN = CO
= DP.
¿Cómo varía el área del cuadrilátero
MNOP cuando M se desplaza sobre el
segmento AB? Calcular su valor
mínimo.
8

9. ¿Por qué en matemática se usan las representaciones?
Los objetos matemáticos, ideales por naturaleza,
no pueden ser captados directamente por los
sentidos, de aquí la necesidad de
representaciones para poder mediar con esos
objetos. En el campo de la matemática se
presentan muchas veces varias representaciones
para un mismo objeto; distinguir la
representación del objeto mismo es fundamental
para que exista comprensión. Cada concepto
matemático necesita para su total comprensión,
del empleo de más de un sistema de
representación. Cada representación, junto con
las reglas que la acompañan, implica una
significación distinta del concepto.
9

10. En los trabajos de R. Duval (1992, 1999) y de las
últimas investigaciones en didáctica de las
matemáticas, se pone en evidencia que el
aprendizaje de un concepto se realiza en una forma
más efectiva si se trabaja con las distintas
representaciones del mismo.
10

11. En el campo de la educación matemática, el concepto
de representación se toma como equivalente a señal
externa que muestra y hace presente un concepto
matemático, también como signo o marca que los
sujetos utilizan para pensar la matemática, también
como esquemas o imágenes mentales con los que la
mente puede trabajar en ideas matemáticas.
Se podría decir que las representaciones semióticas
utilizadas en la matemática son todos los signos o
gráficos que permiten a un sujeto abordar e
interactuar con el conocimiento matemático. El sujeto
las utiliza para registrar y comunicar sus ideas.
11

12. ¿Qué es un registro de representación semiótica?
Un sistema de representación semiótica es entendido
como un sistema de signos que tiene como función
principal la de comunicación. En el caso de la
matemática las representaciones cumplen además,
otras funciones muy importantes que son la de
mediación con los objetos matemáticos y la de
favorecer el entendimiento.
12

13. Para la actividad siguiente, describa detalladamente los
procesos de pensamiento que pone en juego al abordar las
mismas.
Esbozar el gráfico de f+g, sabiendo que f es una función
polinómica de 2º grado. Determinar gráficamente sus
raíces.
13
g
f
Esbozar el gráfico de las funciones f.g, f/g y g/f

14. ¿Qué representa la “parte lineal” de una función
14
polinómica de segundo grado?
¿Y de una de tercer grado?

15. ¿Qué actividades cognitivas debe permitir un
registro de representación?
• Formación de una representación identificable como una
representación de un registro dado.
• El tratamiento de una representación que es la
transformación de esta representación en el registro mismo
donde ha sido formada. El tratamiento es una
transformación interna a un registro. El cálculo es una
forma de tratamiento propio de las escrituras simbólicas.
Dentro de cada registro existen reglas de tratamiento.
• La conversión de una representación es una
transformación de esta representación en una
representación de otro registro conservando la totalidad o
solamente una parte del contenido de la representación
inicial. La conversión es una transformación externa 15
al
registro de partida.

16. 16
¿Qué es construir un concepto?
La construcción de los conceptos matemáticos depende
estrechamente de la capacidad de usar varios registros de
representación semiótica de dichos conceptos:
• De representarlos en un registro dado
• De tratar tales representaciones al interior de un mismo
registro
• De convertir tales representaciones de un registro dado en otro
La coordinación de varios registros de representación semiótica
aparece así como fundamental para una aprehensión conceptual
de los objetos:
• Es necesario no confundir el objeto con sus representaciones y
• Reconocerlo en cada una de sus representaciones
Bajo estas dos condiciones una representación funciona
verdaderamente como una representación, es decir proporciona el
acceso al objeto representado

17. De acuerdo a la reseña histórica vemos que las
relaciones funcionales se pueden representar
mediante tablas, gráficas, expresiones algebraicas,
las cuales son mediadas por el lenguaje cotidiano.
La complejidad del concepto de función se refleja en
las diversas concepciones y diversas
representaciones con las que se enfrentan los
estudiantes y profesores en la actualidad y además
se le puede percibir en las diferentes etapas que en
su evolución ha tomado.
17
Una mirada al concepto de función desde la
Didáctica de la Matemática

18. En cuanto a las representaciones semióticas para las
funciones podemos decir que se materializa a través de
cuatro sistemas de representación. Cada una de ellas
pone en relevancia aspectos distintos del concepto.
Estas representaciones son, según Janvier:
18
• representación gráfica
• representación tabular
• representación analítica
• representación verbal

19. La representación gráfica tiene por excelencia, la
potencialidad del entendimiento que da la
visualización, se relaciona con los aspectos
geométricos y topológicos del concepto.
La representación tabular pone de manifiesto los
aspectos numéricos.
La representación analítica requiere del uso del
lenguaje del álgebra.
La representación verbal es la más natural, la más
próxima a las destrezas comunicativas del
individuo, permite articular a todas las
representaciones y actúa como intérprete de todas
ellas.
19

20. Estas cuatro representaciones semióticas de las
funciones, utilizan códigos diferentes para
manifestar la relación funcional entre las variables.
Estos códigos no son equivalentes, ni en el tipo de
información que codifican, ni en complejidad, ni en
la formación que requiere un estudiante para su
comprensión.
En el aprendizaje del concepto de función será
fundamental lograr que el estudiante comprenda el
sistema semiótico de representación utilizado en
cada caso y desarrolle la capacidad y la destreza de
traducir la información de una representación a
otra.
20

21. Los cuatro sistemas de representación
mencionados más arriba generan dieciséis
posibles conversiones de un sistema a otro o
tratamientos dentro de cada sistema, que se
representan en el siguiente esquema de Janvier:
21

22. Las conversiones de un sistema a otro no se encuentran
en carácter “puro” sino que muchas veces transitamos
otros sistemas para llegar al deseado, siendo el lenguaje
verbal el que actúa como un articulador de los otros
lenguajes. El costo de la tarea cognitiva cambia con el
sentido de la conversión, cada uno de los sistemas de
representación debe ser el objeto de un trabajo de
exploración de las variaciones sistemáticas y de un
trabajo de observación de las variaciones concomitantes.
En general en el aula se realiza este tránsito entre
registros como si se tratara de nociones transparentes,
como nociones intuitivas que no hay necesidad de
explicar, lo que podría generar dificultades de
entendimiento del concepto por parte de los estudiantes.
22

23. El NCTM propone organizar el estudio de las matemáticas
alrededor de dos aspectos fundamentales:
a) Líneas de contenidos:
23
¿Qué nos dice el colectivo docente?
Número
Álgebra
Geometría
Medida
Análisis de datos
y probabilidad
0 - 6 7 - 9 10 - 12 13 - 17

24. b) Incluir actividades o procesos propios del
quehacer matemático como la resolución de
problemas; el razonamiento y la demostración; la
comunicación; las representaciones; las
visualizaciones; la interpretación de diagramas;
la descripción de situaciones; la traducción de
información visual y viceversa; la detección de
invariantes.
Los procesos inherentes a la actividad
matemática se presentan al mismo nivel que los
contenidos.
24

25. El desarrollo de actividades o procesos propios del
quehacer matemático garantiza que
independientemente del tipo de contenidos que
pueda ser vigente dentro de 10 o 20 años, la forma
de interactuar con esos contenidos siempre se
realiza necesariamente a partir de estos procesos.
No importa si el contenido específico es la
ecuación de segundo grado o las ternas
pitagóricas, u otro contenido nuevo: siempre será
de mayor interés visualizar relaciones, buscar
patrones o invariantes, plantear conjeturas, o
establecer argumentos o pruebas.
25

26. 26
Estándares de Álgebra
• Entender patrones, relaciones y funciones.
• Representar y analizar situaciones y
estructuras matemáticas usando símbolos
algebraicos.
• Usar modelos matemáticos para representar y
entender relaciones cuantitativas.
• Analizar el cambio en varios contextos.

27. ENTENDER PATRONES, RELACIONES Y FUNCIONES
Nivel 0 a 6 años
• Ordenar y clasificar objetos por tamaño, número u otras
propiedades.
• Reconocer, describir y continuar patrones así como traducir de
una representación a otra.
• Analizar cómo se generan los patrones.
Nivel 7 a 9 años
• Describir, continuar y hacer generalizaciones sobre los modelos
geométricos y numéricos.
• Representar y analizar patrones y funciones, usando palabras,
tablas, y gráficos.
Nivel 10 a 12 años
• Representar, analizar y generalizar una variedad de patrones con
tablas, gráficos, palabras, y, cuando sea posible, con reglas
simbólicas.
• Relacionar y comparar formas diferentes de representación para
una relación.
• Identificar funciones como ser lineales y no lineales y contrastar
27
sus propiedades a través de tablas, gráficos, o ecuaciones.

28. 28
Nivel 13 a 17 años
• Generalizar patrones a través de funciones definidas por
recurrencia y en su forma explícita.
• Entender relaciones y funciones por medio del uso de varias
representaciones para ellas y adquirir flexibilidad en pasaje de
una representación a otra.
• Analizar funciones de una variable por medio de la investigación
de razones de cambio, ceros, asíntotas y comportamiento local y
global.
• Entender y realizar transformaciones como operaciones
aritméticas, composición e inversión de funciones usando la
tecnología para realizar dichas operaciones con expresiones más
complicadas.
• Entender y comparar las propiedades de clases de funciones
incluyendo las funciones exponenciales, logarítmicas,
polinómicas, racionales y periódicas.
• Interpretar las representaciones de funciones de dos variables.

29. REPRESENTAR Y ANALIZAR SITUACIONES Y ESTRUCTURAS
MATEMÁTICAS USANDO SÍMBOLOS ALGEBRAICOS
Nivel 0 a 6 años
• Ilustrar propiedades de las operaciones, como ser la conmutativa,
usando números específicos.
• Usar representaciones concretas, pictóricas y verbales para
desarrollar una comprensión de las notaciones convencionales o
inventadas.
Nivel 7 a 9 años
• Describir, continuar y hacer generalizaciones sobre los modelos
geométricos y numéricos.
• Representar y analizar patrones y funciones, usando palabras,
tablas, y gráficos.
Nivel 10 a 12 años
• Explorar las relaciones entre las expresiones simbólicas y los
gráficos de rectas.
• Usar el álgebra simbólica para representar situaciones y resolver
29
problemas.

30. 30
Nivel 13 a 17 años
• Entender el significado de formas equivalentes de expresiones,
ecuaciones, inecuaciones y relaciones.
• Escribir formas equivalentes de ecuaciones, inecuaciones y
sistemas de ecuaciones y resolverlos con eficacia ya sea en forma
mental, o con lápiz y papel en casos sencillos y usando la
tecnología en todos los casos.
• Usar el algebra simbólica para representar y explicar relaciones
matemáticas.
• Usar representaciones simbólicas variadas incluyendo
expresiones recursivas y paramétricas para funciones y
relaciones.
• Juzgar el significado, utilidad y razonabilidad de los resultados
obtenidos por medio de la manipulación simbólica incluyendo
aquellos que se obtienen a través de la tecnología.

31. 31
USAR MODELOS MATEMÁTICOS PARA REPRESENTAR
Y ENTENDER RELACIONES CUANTITATIVAS
Nivel 0 a 6 años
• Modelar situaciones que involucren la adición y sustracción
de números enteros usando objetos, pinturas y símbolos.
Nivel 7 a 9 años
• Modelar situaciones problemáticas con objetos y usar
representaciones, como ser gráficas, tablas y ecuaciones, para
arribar a conclusiones.
Nivel 10 a 12 años
• Modelar y resolver problemas contextualizados usando varias
representaciones, como ser tablas, gráficas y ecuaciones.

32. 32
Nivel 13 a 17 años
• Identificar relaciones cuantitativas escenciales en una
situación y determinar la clase o clases de funciones que
pueden modelar dichas relaciones.
• Usar expresiones simbólicas, incluyendo formas iterativas
y recursivas, para representar relaciones provenientes de
diferentes contextos.
• Redactar conclusiones razonables acerca de las situaciones
que han sido modeladas.

33. 33
ANALIZAR EL CAMBIO EN VARIOS CONTEXTOS.
Nivel 0 a 6 años
• Describir cambios cualitativos, como ser el estar más alto.
• Describir cambios cuantitativos, como ser el crecimiento de
“tantos” centímetros en un año.
Nivel 7 a 9 años
• Investigar cómo influye el cambio de una variable en la otra.
• Identificar y describir situaciones con cambios constantes o
variables compararlos.
Nivel 10 a 12 años
• Usar gráficos para analizar la naturaleza de los cambios en las
cantidades en las relaciones lineales.
Nivel 13 a 17 años
• Aproximar e interpretar las razones de cambio de datos gráficos
y numéricos.

34. De Guzmán, M.; Colera, J.; Salvador, A. (1995). Matemáticas.
Bachillerato 1. Madrid: Anaya.
De Guzmán, M.; Colera, J.; Salvador, A. (1995). Matemáticas.
Bachillerato 2. Madrid: Anaya.
Duval, R. (1992). Gráficas y ecuaciones: la articulación de dos
registros. En R. Cambray, E. Sánchez & G. Zubieta (comp.),
Antología en educación matemática, material de apoyo para el
seminario de educación matemática.
Maestría en Ciencias, Especialidad en Matemática Educativa,
Nivel Medio Superior. Cinvestav- IPN. 125-141.
Duval, R. (1999). Semiosis y pensamiento humano. Registros
semióticos y aprendizajes intelectuales. Cap.1. Cali, Colombia:
Universidad del Valle, Grupo de Educación Matemática.
34
Referencias

35. Janvier, C. (1987). Problems of representation in the teaching
and learning of mathematics. Hillsdale, New Jersey: Lawrence
Erlbaum A.P.
National Council of Teachers of Mathematics (2000). Standards
and Principles for School Mathematics. Algebra.
http://www.nctm.org/standards/standards.htm
Youschkevitech, A. P. (1997). El concepto de función hasta la
primera mitad de siglo XIX. Serie de Antologías No. 1. Área de
Nivel Superior (pp. 99-146). México: Departamento de
Matemática Educativa, Cinvestav-IPN. Traducción de R. M.
Farfán de The concept of function up to the middle of the 19th
century. Arch. Hist. Exact. Sci. 16, 37-85.
35