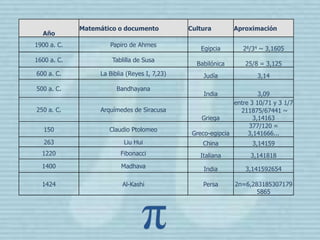
El número pi tiene su origen en las palabras griegas que significan perímetro y circunferencia. A lo largo de la historia, matemáticos de culturas como la egipcia, babilónica, china y europea han calculado aproximaciones de pi usando polígonos inscritos en círculos. Arquímedes fue capaz de determinar pi con un error menor al 0,05% usando un polígono de 96 lados. Pi se usa comúnmente en fórmulas de geometría, trigonometría, probabilidad, física y otras á

2. • Origen del nombre
• Historia
• Usos
• Curiosidades

3. Origen del Nombre
La notación con la letra griega π proviene de la inicial de las
palabras de origen griego "περιφέρεια" (periferia) y
"περίμετρον" (perímetro) de un círculo, notación que fue
utilizada primero por William Oughtred, y propuesto su uso por
el matemático galés William Jones, aunque fue el matemático
Leonhard Euler, con su obra «Introducción al cálculo
infinitesimal» de 1748, quien la popularizó.

4. •Antiguo Egipto: El valor aproximado de π en las antiguas culturas se remonta a
la época del escriba egipcio Ahmes en el año 1800 a. C., descrito en el papiro
Rhind, donde se emplea un valor de π mediante la aproximación del área de un
cuadrado de lado 8, a la de un círculo de diámetro 8.
•Mesopotamia: Algunos matemáticos mesopotámicos empleaban, en el cálculo de
segmentos, valores de igual a 3, alcanzando en algunos casos valores más
aproximados, como el de
•Antigüedad clásica: El matemático griego Arquímedes fue capaz de determinar
el valor de π, con un error que oscila entre 0,024% y 0,040% sobre el valor real. El
método usado por Arquímedes consistía en circunscribir e inscribir polígonos
regulares en circunferencias y calcular el perímetro de dichos polígonos. Llegó a
polígonos de 96 lados.

5. •Matemática china: el matemático Liu Hui fue el primero en sugerir que 3,14 era
una buena aproximación, usando un polígono de 96 o 192 lados. Posteriormente
estimó π como 3,14159 empleando un polígono de 3.072 lados.
•Renacimiento europeo : A partir del siglo XII, con el uso de cifras arábigas en
los cálculos, se facilitó mucho la posibilidad de obtener mejores cálculos para π.
Fibonacci amplifica el método de Arquímedes, proporcionando un intervalo más
estrecho. Algunos matemáticos del siglo XVII, como Viète, usaron polígonos de
hasta 393.216 lados para aproximarse con buena precisión a 3,141592653.
•Época moderna: En 1610 el matemático Ludolph van Ceulen calculó los 35
primeros decimales de π. Se dice que estaba tan orgulloso de esta hazaña que lo
mandó grabar en su lápida. Los libros de matemática alemanes durante muchos
años denominaron a π como número ludolfiano.

6. Matemático o documento Cultura Aproximación
Año
1900 a. C. Papiro de Ahmes
Egipcia 28/34 ~ 3,1605
1600 a. C. Tablilla de Susa
Babilónica 25/8 = 3,125
600 a. C. La Biblia (Reyes I, 7,23) Judía 3,14
500 a. C. Bandhayana
India 3,09
entre 3 10/71 y 3 1/7
250 a. C. Arquímedes de Siracusa 211875/67441 ~
Griega 3,14163
377/120 =
150 Claudio Ptolomeo
Greco-egipcia 3,141666...
263 Liu Hui China 3,14159
1220 Fibonacci Italiana 3,141818
1400 Madhava India 3,141592654
1424 Al-Kashi Persa 2π=6,283185307179
5865

7. Uso en matemáticas y ciencia
•Geometría y trigonometría: Para cualquier círculo de radio r, la longitud de la
circunferencia es 2πr y el área del círculo es πr2. Además, π aparece en fórmulas
para áreas y volúmenes de muchas otras figuras geométricas relacionadas con la
circunferencia, como elipses, esferas, conos, y toroides. π aparece en integrales
definidas que describen la circunferencia, área o volumen de cuerpos de revolución.
En el sistema de medición de ángulos equivale a 180° sexagesimales.
•Probabilidad y estadística: Hay muchas distribuciones cuyas
fórmulas contienen a π. El problema de la aguja de Buffón es llamado
en ocasiones como una aproximación empírica de π.
•Física: Aunque no es una constante física, π aparece rutinariamente en ecuaciones
que describen los principios fundamentales del Universo, Debido en gran parte a su
relación con la naturaleza del círculo y, correspondientemente, con el sistema de
coordenadas esféricas.

8. Curiosidades:
•En el año 1998 aparece una película del director Darren Aronofsky denominada Pi
sobre un matemático que cree que el mundo se representa por números.
•El 14 de marzo (3/14 en formato de fecha de Estados Unidos) se marca también
como el día pi en el que los fans de este número lo celebran con diferentes
actuaciones. Curiosamente es el cumpleaños de Einstein.
•En el año 2002 el japonés Akira Haraguchi rompió el record mundial recitando
durante 13 horas 83.431 dígitos del número pi sin parar y en 2006 volvió a romper
su propio record recitando 100.000 dígitos del número pi, realizando una parada
cada dos horas de 10 minutos para tomar aire.
•En Argentina, el número telefónico móvil para emergencias en estaciones de trenes
y subterráneos es ∗31416