Este documento describe las características de los ácidos y las bases, así como algunas definiciones clave relacionadas con ellos. En primer lugar, se describen las propiedades de los ácidos y las bases, como su sabor, corrosividad y efectos sobre indicadores de pH. Luego, se resumen las teorías de Arrhenius, Brønsted-Lowry y Lewis sobre la naturaleza química de los ácidos y las bases. Finalmente, se explican conceptos como el pH, las disoluciones ácidas y básicas, y los

2. 2
Ácido-Base

3. 3
Características
ÁCIDOS:
 Tienen sabor agrio.
 Son corrosivos para la
piel.
 Enrojecen ciertos
colorantes vegetales.
 Disuelven sustancias
 Atacan a los metales
desprendiendo H2.
 Pierden sus propiedades
al reaccionar con bases.
BASES:
 Tiene sabor amargo.
 Suaves al tacto pero
corrosivos con la piel.
 Dan color azul a ciertos
colorantes vegetales.
 Precipitan sustancias
disueltas por ácidos.
 Disuelven grasas.
 Pierden sus propiedades
al reaccionar con ácidos.

4. ácidos y bases de uso casero
 ácido acético vinagre
ácido acetil salicílico
aspirina
 ácido ascórbico vitamina C
 ácido cítrico zumo de
cítricos
 ácido clorhídrico sal
fumante para limpieza,
jugos gástricos
 ácido sulfúrico baterías
 amoníaco (base)
limpiadores caseros
 hidróxido de magnesio
(base) leche de magnesia
(laxante y antiácido)
 Bicarbonato de sodio
 Hidróxido de sodio
4

5. H+
OH-

6. 6

7. 7

8. Conceptos de ácidos y bases
 Los conceptos de ácido y de base han sido definidos y
ampliados a lo largo del tiempo. Vamos a señalar algunas de
las definiciones dadas:
 1689, Robert Boyle observa algunas de las propiedades
de ácidos y bases:
 los ácidos disuelven muchas sustancias
 cambian de color algunos tintes
 pierden sus propiedades al mezclarse con los álcalis
 1814, Gay-Lussac concluye que los ácidos neutralizan a
las bases.
 1884, August Arrhenius, químico y físico sueco, propone la
teoría de la disociación electrolítica. Esta teoría permite
formular la teoría de las relaciones ácido-base.
Considerando la disolución en agua.

9. TEORÍA DE ARRHENIUS

10. 10
Definición de Arrhenius
 Publica en 1887 su teoría de
“disociación iónica”.
 Hay sustancias (electrolitos) que en disolución se
disocian en cationes y aniones.
 ÁCIDO: Sustancia que en disolución acuosa
disocia cationes H+.
 BASE: Sustancia que en disolución acuosa
disocia aniones OH–.

11. 11
Disociación
 ÁCIDOS:
 AH (en disolución acuosa)  A– + H+
 Ejemplos:
 HCl (en disolución acuosa)  H+ + Cl–
 H2SO4 (en disolución acuosa)  2 H+ + SO4
2–
 BASES:
 BOH (en disolución acuosa)  B + + OH–
 Ejemplo:
 NaOH (en disolución acuosa)  Na+ + OH–

12. Arrhenius propuso que:
Los protones o hidrogeniones H+ no existen realmente aislados en
disolución acuosa, ya que se encuentran unidos a una molécula de
agua dando el ión H3O+ (hidronio u oxonio), que a su vez está
rodeados por moléculas de agua, fenómeno conocido como
hidratación.

15. 15
Neutralización
Se produce al reaccionar un ácido con una base
por formación de agua:
H+ + OH– — H2O
El anión que se disoció del ácido y el catión que
se disoció de la base quedan en disolución
inalterados (sal disociada):
NaOH +HCl — H2O + NaCl (Na+ + Cl–)

18.  En 1923, de forma
independiente, el
danés Johannes
Nicolaus Brønsted y
el inglés Lowry
mejoran la teoría de
Arrhenius,
18
Teoría de Brönsted-Lowry

19. 19
Teoría de Brönsted-Lowry.
 ÁCIDOS:
“Sustancia que en disolución cede H+”.
 BASES:
“Sustancia que en disolución acepta H+”.
H+
Ácidos Bases

20. 20
Par Ácido/base conjugado
 Siempre que una sustancia se comporta como
ácido (cede H+) hay otra que se comporta
como base (captura dichos H+).
 Cuando un ácido pierde H+ se convierte en su
“base conjugada” y cuando una base captura
H+ se convierte en su “ácido conjugado”.
– H+
ÁCIDO (HA) BASE CONJ. (A–)
+ H+
+ H+
BASE (B) ÁC. CONJ. (HB+)
– H+

21. H2O + H2O H3O+ + OH-
+ + + -
+
-
Ión hidronio
Ión hidroxilo

22. Ejemplo de par Ácido/base
conjugado
Disociación de un ácido:
HCl (g) + H2O (l)  H3O+(ac) + Cl– (ac)
 En este caso el H2O actúa como base y el
 HCl al perder el H+ se transforma en Cl– (base
22
conjugada)
Disociación de una base:
NH3 (g) + H2O (l)  NH4
+ + OH–
 En este caso el H2O actúa como ácido pues
cede H+ al NH3 que se transforma en NH4
+
(ácido conjugado)

23. Una misma sustancia puede actuar como ácido y como
base, por ejemplo el H2O.
El agua juega el papel de base en las disoluciones acuosas
de ácidos.
CH3COOH + H2O CH3COO- + H3O+
(ácido) (base) (base conjugada) (ácido
conjugado)
En las disoluciones acuosas de bases, la base es la que
acepta un protón, el agua actúa como ácido cediendo un
protón.
+ + OH-
NH3 + H2O NH4
(base) (ácido) (ácido conjugado) (base conjugada)
La reacción de transferencia de un protón de un ácido a
una base se conoce como protólisis.

24. 1923, G. N. Lewis químico norteamericano,
amplia el concepto de ácido y base a
reacciones en las que no hay transferencia
de protones.
Introduciendo con esto el concepto:
mecanismos de reacción en química
orgánica.
24

25. 25
Teoría de Lewis ()
ÁCIDOS:
 “Sustancia que contiene al menos un átomo
capaz de aceptar un par de electrones y formar
un enlace covalente coordinado”.
BASES:
 “Sustancia que contiene al menos un átomo
capaz de aportar un par de electrones para
formar un enlace covalente coordinado”.

26. .
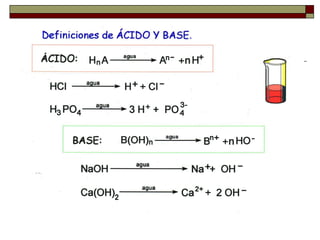
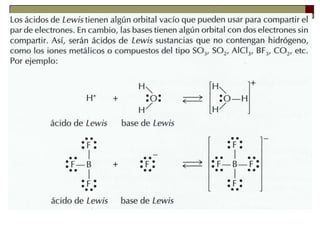
– Acido es una sustancia que puede aceptar un par de
electrones. Es lo que hemos llamado electrófilo.
– Base es una sustancia que puede donar, o compartir, un par
de electrones. Es lo que hemos llamado nucleófilo.
BF3 + F- ( BF4 )-
(ácido) (base)
Ag+ + 2 CN- [Ag (CN)2 ]-
(ácido) (base)

27.  El ácido debe tener su octeto incompleto, y la base
debe tener un par de electrones sin compartir.
 La unión del ácido y la base corresponde a la
formación de un enlace coordinado o dativo. Muchas
reacciones orgánicas se explican por este
comportamiento ácido (electrófilo) o básico
(nucleófilo).
 En disolución acuosa o en disolventes hidrogenados
como el amoniaco líquido, o los alcoholes, no es
necesario recurrir a esta teoría, y se emplea la teoría
de Brönsted y Lowry.

29. 29
Teoría de Lewis (cont.)
 De esta manera, sustancias que no tienen
átomos de hidrógeno, como el AlCl3 pueden
actuar como ácidos:
 AlCl3 + :NH3 Cl3Al:NH3
 Cl H Cl H
| | | |
Cl–Al + : N–H  Cl–AlN–H
| | | |
Cl H Cl H

30. 30
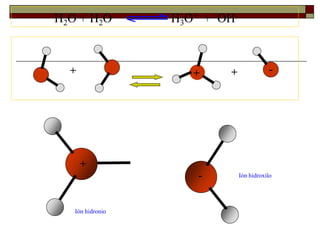
Equilibrio de ionización del agua.
 La experiencia demuestra que el agua tiene una
pequeña conductividad eléctrica lo que indica que
está parcialmente disociado en iones:
 2 H2O (l)  H3O+(ac) + OH– (ac)
 H3O+ · OH–
Kc = ——————
H2O2
 Como H2O es constante por tratarse de un
líquido, llamaremos Kw = Kc · H2O2
  [ ]×[ ] -
w 3 K H O OH
 conocido como “producto iónico del agua”

31. 31
Concepto de pH.
El valor de dicho producto iónico del agua es:
KW (25ºC) = 10–14 M2
En el caso del agua pura:
———–
H3O+ = OH– =  10–14 M2 = 10–7 M
Se denomina pH a:
3 pH log [H O ]   
para el caso de agua pura, como H3O+=10–7 M
pH = – log 10–7 = 7

32. 32
Tipos de disoluciones
 Ácidas: H3O+ > 10–7 M  pH < 7
 Básicas: H3O+ < 10–7 M  pH > 7
 Neutras: H3O+ = 10–7 M  pH = 7
En todos los casos: Kw = H3O+ · OH–
luego si H3O+ aumenta (disociación de un
ácido), entonces OH– debe disminuir para
que el producto de ambas concentraciones
continúe valiendo 10–14 M2

33. 33

34. 34
Gráfica de pH en sustancias
comunes
ÁCIDO BÁSICO
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Zumo de
limón Cerveza
Leche
Agua mar
Sangre
Amoniaco
Agua destilada

35. 35
Concepto de pOH.
 A veces se usa este otro concepto, casi
idéntico al de pH:
pOH log [OH ]   
 Como Kw = H3O+ · OH– = 10–14 M2
 Aplicando logaritmos y cambiando el signo
tendríamos:
 pH + pOH = 14
 para una temperatura de 25ºC.

36. Ejemplo: El pH de una disolución acuosa es 12,6.
¿Cual será la OH– y el pOH a la temperatura de
25ºC?
 pH = – log H3O+ = 12,6, de donde se deduce
que: H3O+ = 10–pH = 10–12,6 M = 2,5 · 10–13 M
36
 Como Kw = H3O+ · OH– = 10–14 M2
 entonces:
 KW 10–14 M2
OH– = ——— = —————— = 0,04 M
H3O+ 2,5 · 10–13 M
 pOH = – log OH– = – log 0,04 M = 1,4
 Comprobamos como pH + pOH = 12,6 + 1,4 =
14

37. Ejercicio A: Una disolución de ácido sulfú-rico tiene
una densidad de 1,2 g/ml y una riqueza del 20 % en
peso. a) Calcule su concentración expresada en
moles/litro y en gramos/litro. b) Calcule el pH de una
disolución preparada diluyendo mil veces la anterior.
37
Problema de
Selectividad
(Marzo 97)
a) ms ms % = —— x 100 = ——— x 100 
mdn Vdn x d
ms % x d 20 x 1,2 g
conc (g/L) = —— = —— = ————— = 240 g/L
Vdn 100 10–3 L x 100
ns ms conc(g/L) 240 g/L
Molaridad = —— = ——— = ———— = ————
Vdn Vdn x Ms Ms 98 g/mol
Molaridad = 2,45 mol/L
b) pH = –log [H3O+] = –log (2 x 2,45x10–3 M) = 2,35

38. 38
Electrolitos fuertes y débiles
 Electrolitos fuertes: ()
Están totalmente disociados
 Ejemplos: HCl (ac)  Cl– + H+
NaOH (ac)  Na+ + OH–
 Electrolitos débiles: ()
Están disociados parcialmente
 Ejemplos: CH3–COOH (ac)  CH3–COO– +
H+
NH3 (ac)+ H2O  NH4
+ + OH–

39. 39
Electrolitos fuertes y débiles
Ácido fuerte
[A–] [H+]
[A–] [H+]
[HA] [HA]
[HA]
Ácido débil

40. 40
Ejemplo: Justifica porqué el ión HCO3
–
actúa como ácido frente al NaOH y como base
frente al HCl.
 El NaOH proporciona OH– a la disolución:
 NaOH (ac)  Na+ + OH–
 por lo que HCO3
–
+ OH–  CO3
2–
+ H2O
– actúa como ácido.
 es decir, el ión HCO3
 El HCl proporciona H+ a la disolución:
 HCl (ac)  H+ + Cl–
 por lo que HCO3
–
+ H+ H2CO3 (CO2 + H2O)
– actúa como base.
 es decir, el ión HCO3

41. 41
Fuerza de ácidos.
 En disoluciones acuosas diluidas (H2O 
constante) la fuerza de un ácido HA depende
de la constante de equilibrio:
 HA + H2O  A– + H3O+
A– · H3O+ A– · H3O+
Kc = ——————  Kc · H2O = —————
—
HA · H2O HA
  
A H O
   3
K H O K
2
[ ] [ ]
[ ]
C [ HA
] a
constante de
 disociación
(K acidez)

42. 42
Fuerza de ácidos (cont.).
 Según el valor de Ka hablaremos de ácidos
fuertes o débiles:
 Si Ka > 100  El ácido es fuerte y estará
disociado casi en su totalidad.
 Si Ka < 1  El ácido es débil y estará sólo
parcialmente disociado.
 Por ejemplo, el ácido acético (CH3–COOH)
es un ácido débil ya que su Ka = 1,8 · 10–5
M

43. 43
Ácidos polipróticos
 Son aquellos que pueden ceder más de un
H+. Por ejemplo el H2CO3 es diprótico.
 Existen pues, tantos equilibrios como H+
disocie:
 H2CO3 + H2OHCO3
– + H3O+
– + H2OCO3
 HCO3
2– + H3O+
–  · H3O+ CO3
 HCO3
2–  · H3O+
Ka1 = ———————— Ka2 = ———————
H2CO3 HCO3
– 
 Ka1 = 4,5 · 10–7 M Ka2 = 5,7· 10–11 M
 La constantes sucesivas siempre van
disminuyendo.

44. Ejemplo: Sabiendo que las constantes de acidez del
ácido fosfórico son: Ka1 = 7,5 x 10–3, Ka2 = 6,2 x 10–8 y
Ka3 = 2,2 x 10–13, calcular las concentraciones de los
iones H3O+, H2PO4
K M
44
–, HPO4
2– y PO4
3– en una disolución
de H3PO4 0,08 M.
Equilibrio 1: H3PO4 + H2O  H2PO4
– + H3O+
c. in.(mol/l): 0,08 0 0
c. eq.(mol/l): 0,08 – x x x
 
[ ] [ ]
H PO H O x
2 4 3 3
 x = 0,021
2
 
   

1
3 4
7,5 10
[ ] 0,08 a
H PO x
    2 4 3 [H PO ] [H O ] 0,021M

45. 2
4 3 8
K M
[ ] [ ] (0,021 ) 0,021
H PO H O z z z
; 3 4 3 13
K M
45
Equilibrio 2: H2PO4
– + H2O  HPO4
2– + H3O+
c. in.(mol/l): 0,021 0 0,021
c. eq.(mol/l): 0,021 – y y 0,021 + y
 
[ ] [ ] (0,021 ) 0,021
HPO H O y y y
  
   
 y = 6,2 x 10–8 M
Equilibrio 3: HPO4
2– + H2O  PO4
3– + H3O+
c. in.(mol/l): 6,2 x 10–8 0 0,021
c. eq.(mol/l): 6,2 x 10–8– z z 0,021 + z
  
   
2 2 8 8
 z = 6,5 x 10–19 M



;
2
2 4
6,2 10
a
[ H PO ] 0,021 y
0,021     2 8
4 [HPO ] 6,2 10 M


  
  
4
2,2 10
a
[ HPO ] 6,2 10 z
6,2 10     3 19
4 [PO ] 6,5 10 M

46. 46
Fuerza de bases.
 En disoluciones acuosas diluidas (H2O 
constante) la fuerza de una base BOH
depende de la constante de equilibrio:
 B + H2O  BH+ + OH–
 BH+ x OH– BH+ x OH–
Kc = ——————  Kc x H2O = —————
—
B x H2O B
  
[ BH ] [ OH
]
K [ H O ]
K
   2
C [ B
] b
 (K basicidad)

47. 47
Fuerza de ácidos y bases (pK)
 Al igual que el pH se denomina pK a:
 pKa= – log Ka ; pKb= – log Kb
 Cuanto mayor es el valor de Ka o Kb
mayor es la fuerza del ácido o de la base.
 Igualmente, cuanto mayor es el valor de
pKa o pKb menor es la fuerza del ácido o de
la base.

48. 48
Ejemplo: Determinar el pH y el pOH de una
disolución 0,2 M de NH3 sabiendo que Kb
(25ºC) = 1,8 · 10–5 M
 Equilibrio: NH3 + H2O  NH4
+ + OH–
 conc. in.(mol/l): 0,2 0 0
 conc. eq.(mol/l): 0,2 – x x x
+ x OH– x2
 NH4
Kb = ——————— = ——— = 1,8 x 10–5 M
NH3 0,2 – x
 De donde se deduce que x = OH– = 1,9 x 10–3 M
 pOH = – log OH– = – log 1,9 x 10–3 = 2,72
 pH = 14 – pOH = 14 – 2,72 = 11,28

49. 49
Relación entre Ka y Kb conjugada
 Equilibrio de disociación de un ácido:
 HA + H2O  A– + H3O+
 Reacción de la base conjugada con el agua:
 A– + H2O  HA + OH–
 A– x H3O+ HA x OH–
Ka = —————— ; Kb = ——————
HA A–
 A– x H3O+ x HA x OH–
Ka x Kb = ———————————— = KW
HA x A–

50. 50
Relación entre Ka y Kb conjugada
(cont.).
 En la práctica, esta relación (Ka x Kb = KW)
significa que:
 Si un ácido es fuerte su base conjugada es
débil.
 Si un ácido es débil su base conjugada es
fuerte.
 A la constante del ácido o base conjugada en
la reacción con el agua se le suele llamar
constante de hidrólisis (Kh).

51. Ejemplo: Calcular la Kb del KCN si sabemos que la
51
Ka del HCN vale 4,9 · 10–10 M.
 El HCN es un ácido débil (constante muy
pequeña). Por tanto, su base conjugada, el
CN–, será una base relativamente fuerte. Su
reacción con el agua será:
 CN– + H2O  HCN + OH–
 KW 10–14 M2
Kb = —— = —————— = 2,0 x 10–5 M
Ka 4,9 x 10–10 M

52. 52
Relación entre la constante
y el grado de disociación “”
 En la disociación de un ácido o una base
   
A H O c c c
  
  
 Igualmente:
 En el caso de ácidos o bases muy débiles
(Ka/c o Kb/c < 10–4),  se desprecia frente
a 1 con lo que: Ka = c 2 (Kb = c 2 )
 De donde:
b
c
K




2
1

2
3
1 1
[ ] [ ]
[ ] ( - ) a
K
HA c
 
 a K
  b K
c
c


53. Ejemplo: Una disolución de HBO2 10-2 M
tiene un de pH de 5,6. a) Razone si el ácido y su base
conjugada serán fuertes o débiles. b) Calcule la constante de
disociación del ácido (Ka). c) Cal-cule, si es posible, la
constante de basicidad del ion borato (Kb). d) Si 100 ml de
esta disolución de HBO2 se mezclan con 100 ml de una
disolución 10-2 M de hidróxido sódico, ¿qué concentración
de la base conjugada se obtendrá?
53
a) [H3O+] = 10–pH = 10–5,6 = 2,51 x 10–6 M
 =[HO+]/c = 2,51 x 10–6 M/ 10-2 M = 2,51 x10–4
3lo que significa que está disociado en un 0,025 %
luego se trata de un ácido débil. Su base conjugada,
BO–, será pues, relativamente fuerte.
2
b) Ka = c x 2 = 10-2 M x(2,51 x 10–4)2 = 6,3 x 10–10
c) Kb = Kw/Ka = 10–14/ 6,3 x 10–10 = 1,58 x 10–5
d) Se neutralizan exactamente: [BO2
–] = 5 x 10–3 M
Problema de
Selectividad
(Marzo 98)

54. 54
matraces, uno conteniendo 15 ml de HCl cuya
concentración es 0,05 M y el otro 15 ml de ácido etanoico
(acético) de concentración 0,05 M
a) Calcule el pH de cada una de ellas. b) ¿Qué cantidad de
agua se deberá añadir a la más ácida para que el pH de las dos
disoluciones sea el mismo? Dato: Ka (ácido etanoico) = 1,8 x
10-5
a) HCl es ácido fuerte luego está totalmente disociado,
por lo que [H3O+] = 0,05 M
pH = –log [H3O+] = –log 0,05 = 1,30
CH3COOH es ácido débil por lo que:
Ka 1,8 ·10-5 M
 = —— = ————— = 0,019
c 0,05 M
[H3O+] = c  = 0,05 M x 0,019 = 9,5 x 10-4 M
pH = –log [H3O+] = –log 9,5 x 10-4 = 3,0
Problema
Selectividad
(Junio 98)

55. 55
matraces, uno conteniendo 15 ml de HCl cuya
concentración es 0,05 M y el otro 15 ml de ácido etanoico
(acético) de concentración 0,05 M
a) Calcule el pH de cada una de ellas. b) ¿Qué cantidad de
agua se deberá añadir a la más ácida para que el pH de las dos
disoluciones sea el mismo? Dato: Ka (ácido etanoico) = 1,8 x
10-5
b) n (H3O+) en HCl = V x Molaridad = 0,015 l x 0,05 M =
= 7,5 x 10-4 mol.
Para que el pH sea 3,0 [H3O+] = 10-3 M que será también
la [HCl] ya que está totalmente disociado.
El volumen en el que deberán estar disueltos estos moles es:
V = n/Molaridad = 7,5 x 10-4 mol/ 10-3 mol·l-1 = 0,75 litros
Luego habrá que añadir (0,75 – 0,015) litros = 735 ml
Problema
Selectividad
(Junio 98)

56. 56
Hidrólisis de sales
 Es la reacción de los iones de una sal con el
agua.
 Sólo es apreciable cuando estos iones
proceden de un ácido o una base débil:
 Hidrólisis ácida (de un catión):
 NH4
+ + H2O  NH3 + H3O+
 Hidrólisis básica (de un anión):
 CH3–COO– + H2O  CH3–COOH + OH–

57. Tipos de hidrólisis.
 Según procedan el catión y el anión de un
ácido o una base fuerte o débil, las sales se
clasifican en:
 Sales procedentes de ácido fuerte y base fuerte.
57
 Ejemplo: NaCl
 Sales procedentes de ácido débil y base fuerte.
 Ejemplo: NaCN
 Sales procedentes de ácido fuerte y base débil.
 Ejemplo: NH4Cl
 Sales procedentes de ácido débil y base débil.
 Ejemplo: NH4CN

58. Sales procedentes de ácido fuerte
y base fuerte.
58
 Ejemplo: NaCl
 NO SE PRODUCE HIDRÓLISIS ya que
tanto el Na+ que es un ácido muy débil
como el Cl– que es una base muy débil
apenas reaccionan con agua. Es decir los
equilibrios:
 Na+ + 2 H2O NaOH + H3O+
 Cl– + H2O HCl + OH–
 están muy desplazado hacia la izquierda.

59. Sales procedentes de ácido débil
y base fuerte.
59
 Ejemplo: Na+CH3–COO–
 SE PRODUCE HIDRÓLISIS BÁSICA ya
que el Na+ es un ácido muy débil y apenas
reacciona con agua, pero el
CH3–COO– es una base fuerte y si reacciona
con ésta de forma significativa:
 CH3–COO– + H2O  CH3–COOH+ OH–
 lo que provoca que el pH > 7 (dis. básica).

60. Sales procedentes de ácido fuerte
y base débil.
60
 Ejemplo: NH4Cl
 SE PRODUCE HIDRÓLISIS ÁCIDA ya
+ es un ácido relativamente fuerte
que el NH4
y reacciona con agua mientras que el Cl– es
una base débil y no lo hace de forma
significativa:
+ + H2O  NH3 + H3O+
 NH4
 lo que provoca que el pH < 7 (dis. ácida).

61. Sales procedentes de ácido débil
y base débil.
61
 Ejemplo: NH4CN
+ como el
 En este caso tanto el catión NH4
anión CN– se hidrolizan y la disolución será
ácida o básica según qué ion se hidrolice en
mayor grado.
 Como Kb(CN–) = 2 · 10–5 M y
+) = 5,6 · 10–10 M, en este caso, la
Ka(NH4
disolución es básica ya que K(CN–) es mayor
bque K(NH+)
a4

62. 62
Ejemplo: Sabiendo que Ka (HCN) = 4,0 · 10–10 M,
calcular el pH y el grado de hidrólisis de una
disolución acuosa de NaCN 0,01 M. 
 La reacción de hidrólisis será:
 CN– + H2O  HCN+ OH–
 HCN · OH– KW
Kh(CN–) = —————— = —————— =
CN– 4,0 · 10–10 M
 1 · 10–14 M2
Kh(CN–) = —————— = 2,5 · 10–5 M
4,0 · 10–10 M

63. 63
Ejemplo: Sabiendo que Ka (HCN) = 4,0 · 10–10 M,
calcular el pH y el grado de hidrólisis de una
disolución acuosa de NaCN 0,01 M. 
 CN– + H2O  HCN + OH–
 Conc inin. (M) 0,01 0 0
 Conc equil. (M) 0,01(1–) 0,01  0,01 
 HCN x OH– (0,01 )2 M2
2,5 · 10–5 M = —————— = ——————
CN– 0,01(1–)M
 Despreciando  frente a 1, se obtiene que  = 0,05
 KW 10–14 M2
H3O+ = ——— = —————— = 2,0 x 10–11
M
OH– 0,01 M x 0,05
 pH = – log H3O+ = – log 2,0 x 10–11 M = 10,7

64. – ni el catión Na+ reaccionan con agua por
64
Ejercicio C: Razone utilizando los equilibrios
correspondientes, si los pH de las disoluciones que se
relacionan seguidamente son ácidos, básicos o neutros. a)
Acetato potásico 0,01 M; b) Nitrato sódico 0,01 M; c)
Sulfato amónico
0,01 M; d) Hidróxido de bario 0,01 M.
a) Acetato potásico: pH básico, ya que
CH3–COO– + H2O  CH3–COOH+ OH–
por ser el ác. acetico débil, mientras que el K+ no
reacciona con agua por ser el KOH base fuerte.
b) nitrato sódico: pH neutro, ya que ni el anión
NO3
proceder el primero del HNO3 y del NaOH el
segundo, ambos electrolitos fuertes.
Problema de
Selectividad
(Septiembre 98)

65. 2– no
65
Ejercicio C: Razone utilizando los equilibrios
correspondientes, si los pH de las disoluciones que se
relacionan seguidamente son ácidos, básicos o neutros. a)
Acetato potásico 0,01 M; b) Nitrato sódico 0,01 M; c)
Sulfato amónico
0,01 M; d) Hidróxido de bario 0,01 M.
c) Sulfato amónico: pH ácido, ya que
NH4
+ + H2O  NH3 + H3O+
por ser el amoniaco débil, mientras que el SO4
reacciona con agua por ser el H2SO4 ácido fuerte.
d) hidróxido de bario: pH básico pues se trata de una
base fuerte (los hidróxidos de los metales alcalinos
y alcalino-térreos son bases bastantes fuertes)
Problema de
Selectividad
(Septiembre 98)

66. 66
Disoluciones amortiguadoras
(tampón) 
 Son capaces de mantener el pH después de
añadir pequeñas cantidades tanto de ácido
como de base. Están formadas por:
 Disoluciones de ácido débil + sal de dicho
ácido débil con catión neutro:
 Ejemplo: ácido acético + acetato de sodio.
 Disoluciones de base débil + sal de dicha
base débil con anión neutro:
 Ejemplo: amoniaco y cloruro de amonio.

67. 67
Variación del pH al añadir pequeñas
cantidades de NaOH o HCl
© Ed. Santillana

68. Ejemplo: Calcular el pH de una disolución tampón
68
formada por una concentración
0,2 M de ácido acético y 0,2 M de acetato de
sodio. Ka (CH3–COOH) = 1,8 · 10–5 M. 
 El acetato está totalmente disociado:
 CH3–COONa  CH3–COO– + Na+
 El ácido acético se encuentra en equilibrio
con su base conjugada (acetato):
 H2O + CH3–COOH  CH3–COO– + H3O+
 cin (M) 0,2 0,2 0
 ceq (M) 0,2 – x 0,2 + x x

69. Ejemplo: Calcular el pH de una disolución tampón
69
formada por una concentración
0,2 M de ácido acético y 0,2 M de acetato de
sodio. Ka (CH3–COOH) = 1,8 · 10–5 M 
 CH3–COO–  · H3O+ (0,2+x) · x M2
1,8 · 10–5 M = ————————— = ——————
CH3–COOH (0,2 – x) M
 De donde se deduce que:
 x = H3O+ = 1,8 · 10–5 M
 pH = – log H3O+ = 4,74

70. 72
Indicadores de pH
(ácido- base) 
 Son sustancias que cambian de color al
pasar de la forma ácida a la básica:
 HIn + H2O  In– + H3O+
forma ácida forma básica
 El cambio de color se considera apreciable
cuando [HIn] > 10·[In–] o [HIn]< 1/10·[In–
]
 In– · H3O+ HIn
Ka = ——————   H3O+  = Ka · ———
HIn In–

71. 73
Algunos indicadores de pH
Indicador
Color forma
ácida
Color forma
básica
Zona de
viraje
(pH)
Violeta de
metilo
Amarillo Violeta 0-2
Rojo Congo Azul Rojo 3-5
Rojo de
metilo
Rojo Amarillo 4-6
Tornasol Rojo Azul 6-8
Fenolftaleína Incoloro Rosa 8-10

72. 74
Valoraciones ácido-base
 Valorar es medir la
concentración de un
determinado ácido o
base a partir del
análisis volumétrico
de la base o ácido
utilizado en la
reacción de
neutralización.

73. 75
Gráfica de valoración de vinagre
con NaOH
Zona de viraje fenolftaleína
20 40 60 V NaOH(ml)
pH
12
10
8
6
4
2

74. 76
Valoraciones ácido-base.
 La neutralización de un ácido/base con una
base/ácido de concentración conocida se
consigue cuando n(OH–) = n(H3O+).
 La reacción de neutralización puede
escribirse:
b HaA + a B(OH)b  BaAb + a·b H2O
 En realidad, la sal BaAb (aBb+ + bAa–) se
encuentra disociada, por lo que la única
reacción es: H3O+ + OH–  2 H2O
n(ácido) x a = n(base) x b

75. 77
Valoraciones ácido-base
 Vácido x [ácido] x a = Vbase x [base] x b
 Todavía se usa mucho la concentración
expresada como Normalidad:
 Normalidad = Molaridad x n (H u OH)
 Vácido x Nácido = Vbase x Nbase
 En el caso de sales procedentes de ácido o
base débiles debe utilizarse un indicador
que vire al pH de la sal resultante de la
neutralización.
Simulación

76. 78
Ejemplo: 100 ml de una disolución de H2SO4 se
neutralizan con 25 ml de una disolución 2 M de
Al(OH)3 ¿Cuál será la [H2SO4]?
3 H2SO4 + 2 Al(OH)3  3SO4
2– +2Al3+ + 6 H2O
 25 ml x 2 M x 3 = 100 ml x Mácido x 2
 De donde:
 25 ml x 2 M x 3
Mácido = ——————— = 0,75 M
100 ml x 2
 [H2SO4] = 0,75 M
 Vácido x Nácido = Vbas x Nbase (Nbase= 3 x Mbase)
 100 ml x Nácido = 25 ml x 6 N
 Nácido = 1,5 N  Mácido= Nácido/2 = 0,75
M
Vídeo

77. 79
Ejemplo: 100 ml de una disolución de H2SO4 se
neutralizan con 25 ml de una disolución 2 M de
Al(OH)3 ¿Cuál será la [H2SO4]?
 Podríamos haber calculado n(H2SO4) a
partir del cálculo estequiométrico, pues
conocemos
n(Al(OH)3 = V· M = 25 ml · 2 M = 50
mmoles
3 H2SO4 + 2 Al(OH)3  3SO4
2– +2Al3+ + 6 H2O
3 mol H2SO4 2 mol Al(OH)3 ————— = ——————
n(H2SO4) 50 mmoles
 n(H2SO4) = 75 mmol
 n (H2SO4) 75 mmol
[H2SO4] = ————— = ———— = 0,75 M

78. 80
Ejercicio D: Si 10,1 ml de vinagre han
necesitado 50,5 ml de una base 0,2 N para su
neutralización. a) Cuál será la normalidad del ácido en el
vinagre; b) Suponiendo que su acidez se debe al ácido
acético (ácido etanoico). ¿Cuál es el porcentaje en peso del
ácido acético si la densidad del vinagre es de 1,06 g/ml?
Problema de
Selectividad
(Septiembre 97)
 a) Vácido x Nácido = Vbase x Nbase
50,5 ml x 0,2 N
Nácido = —————— = 1 N Mácido = 1 M
10,1 ml
 b) Supongamos que tenemos un litro de vinagre:
 m(á. acético) = Molaridad x M x V =
= 1 mol/L x 60 g/mol x 1 L = 60 g
 msoluto 60 g
%= ———— x 100 = ——— x 100 = 5,66 %
mdisolución 1060 g