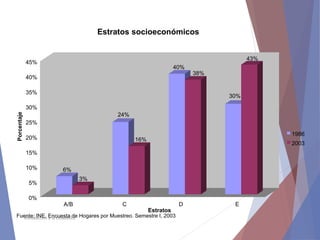
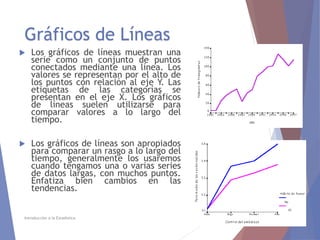
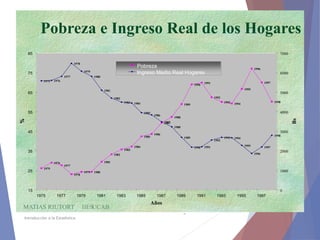
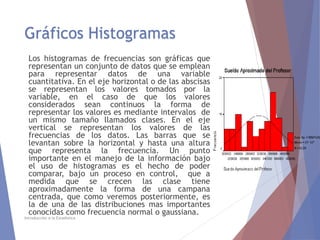
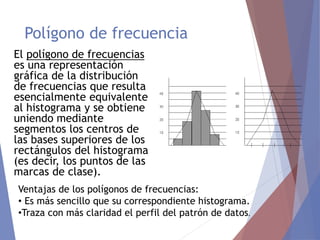
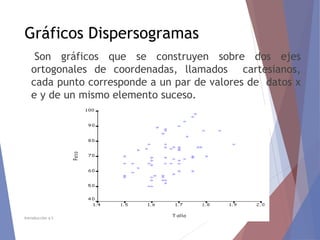
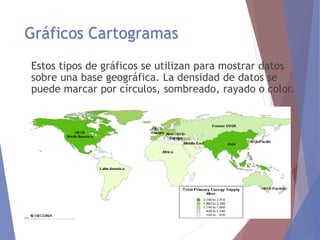
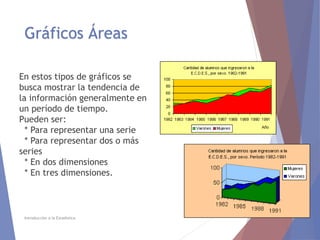
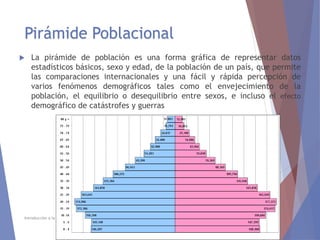
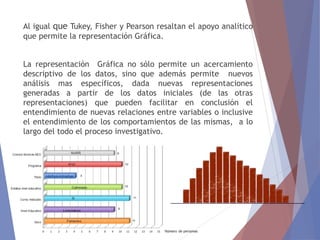
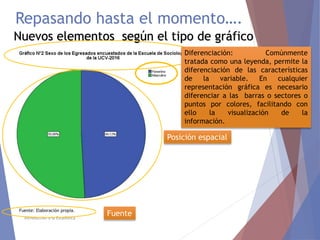
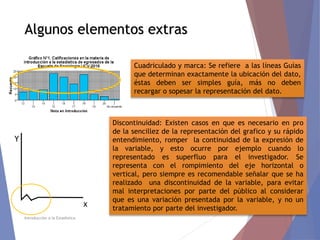
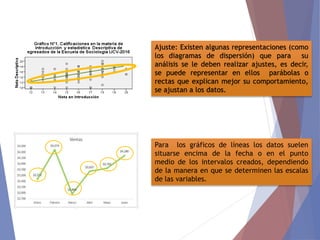
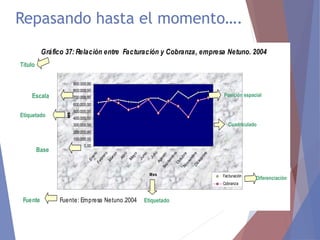
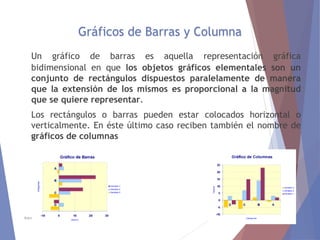
El documento describe diferentes tipos de representaciones gráficas de datos estadísticos. Explica que la representación gráfica ofrece una forma clara de entender conclusiones a partir de datos numéricos y que ha sido promovida por figuras como Tukey. Luego define elementos comunes de los gráficos como título, etiquetas de ejes y fuente. Finalmente describe gráficos específicos como de barras, líneas, sectores e histogramas, detallando sus características y usos.

1. Introducción a la Estadística
La representación de datos de forma gráfica ofrece mensajes más
claros donde las conclusiones son fáciles de entender
La representación gráfica es considerada como una
serie de métodos que permiten la exploración,
análisis y presentación de hechos numéricos por
medio de diversos elementos como puntos, líneas o
símbolos.

2. Este tipo de representación de los datos es muy utilizada en las ciencias sociales, uno de
los principales precursores de su uso y defensa es Tukey, quien logra destacar un análisis a
dicha representación grafica, dando un mayor valor al mismo; al lograr sobrepasar una
simple representación en un entendimiento visual del dato, permitiendo realizar un
primer acercamiento exploratorio a la realidad numérica de la que se hace referencia.
Tukey identifica las ventajas más resaltantes del uso de gráficos:
Ventajas
Es flexible
Son
accesibles a
todo tipo de
público
Resaltan
aspectos
inesperados(
variaciones
positivas o
negativas de
los datos)

3. Al igual que Tukey, Fisher y Pearson resaltan el apoyo analítico
que permite la representación Gráfica.
La representación Gráfica no sólo permite un acercamiento
descriptivo de los datos, sino que además permite nuevos
análisis mas específicos, dada nuevas representaciones
generadas a partir de los datos iniciales (de las otras
representaciones) que pueden facilitar en conclusión el
entendimiento de nuevas relaciones entre variables o inclusive
el entendimiento de los comportamientos de las mismas, a lo
largo del todo el proceso investigativo.

4. Fuente: Elaboración propia.
Elementos de un Gráfico Estadístico
Los elementos fundamentales de un gráfico estadístico dependerán del
tipo de gráfico que se utilice, sin embargo hay elementos en común como
se vera a continuación:
Numero, Titulo y Subtitulo: El titulo debe
reflejar la temática de la investigación y
por ende del dato, es decir, debe responder
¿Qué? Se representa. ¿Cuándo? En periodo
temporal. ¿Dónde? de lugar referido,
evidentemente en los casos a los que es
posible explicar el tiempo y lugar. Su
ubicación es en la parte superior central del
gráfico y los subtítulos debajo del título.
Etiquetado de los ejes: En caso que se usen
representaciones con ejes horizontales y
verticales ambos deben estar etiquetados
para explicar que representan cada uno de
ellos, además es necesario resaltar la
unidad de medida en la que se expresa.
Fuente: Representa la procedencia de los datos, en caso
que el dato sea elaborado por el propio investigador suele
colocarse en la fuente: Elaboración Propia.
Base: Es obligatorio el uso de la
base cero (0) para la graficación
con escalas, y la misma debe
estar representada con líneas
mas gruesas que el resto, para
diferencias fácilmente que ella es
la base y no líneas de
cuadriculado.
Rangos: Además del cero, evidentemente es
necesario determinar en las representaciones de
escala, el rango de los datos, determinando que el
rango contengan el valor máximo y mínimo de
expresión de la variable (todos los datos) para
evitar la representación equivocada por omisión de
algún dato o una representación inentendible por
el uso de escalas inapropiadas a la forma de
expresión de los datos.
Posición espacial: Para el caso de gráficas de
barra, se refiere a la forma en que se
representan los valores de la variable, suelen
ordenarse de menor a mayor o de acuerdo a
los objetivos con la separación entre barras
de acuerdo a la visualización.

5. Repasando hasta el momento….
Introducción a la Estadística
Fuente: Elaboración propia.
Titulo
Fuente
Posición espacial
Nuevos elementos según el tipo de gráfico
Diferenciación: Comúnmente
tratada como una leyenda, permite la
diferenciación de las características
de la variable. En cualquier
representación gráfica es necesario
diferenciar a las barras o sectores o
puntos por colores, facilitando con
ello la visualización de la
información.

6. Algunos elementos extras
Introducción a la Estadística
Cuadriculado y marca: Se refiere a las líneas Guías
que determinan exactamente la ubicación del dato,
éstas deben ser simples guía, más no deben
recargar o sopesar la representación del dato.
Discontinuidad: Existen casos en que es necesario en pro
de la sencillez de la representación del grafico y su rápido
entendimiento, romper la continuidad de la expresión de
la variable, y esto ocurre por ejemplo cuando lo
representado es superfluo para el investigador. Se
representa con el rompimiento del eje horizontal o
vertical, pero siempre es recomendable señalar que se ha
realizado una discontinuidad de la variable, para evitar
mal interpretaciones por parte del público al considerar
que es una variación presentada por la variable, y no un
tratamiento por parte del investigador.
x
Y

7. Ajuste: Existen algunas representaciones (como
los diagramas de dispersión) que para su
análisis se le deben realizar ajustes, es decir,
se puede representar en ellos parábolas o
rectas que explican mejor su comportamiento,
se ajustan a los datos.
Para los gráficos de líneas los datos suelen
situarse encima de la fecha o en el punto
medio de los intervalos creados, dependiendo
de la manera en que se determinen las escalas
de las variables.

8. Gráfico 37: Relación entre Facturación y Cobranza, empresa Netuno. 2004
Facturacion y Cobranza 2004
0,00
100.000,00
200.000,00
300.000,00
400.000,00
500.000,00
600.000,00
700.000,00
800.000,00
900.000,00
E
n
e
r
o
F
e
b
r
e
r
o
M
a
r
z
o
A
b
r
i
l
M
a
y
o
J
u
n
i
o
J
u
l
i
o
A
g
o
s
t
o
S
e
p
t
i
e
m
b
r
e
O
c
t
u
b
r
e
N
o
v
i
e
m
b
r
e
D
i
c
i
e
m
b
r
e
Mes
M$
Facturación
Cobranza
Fuente Fuente: Empresa Netuno.2004
Titulo
Escala
Base
Etiquetado
Etiquetado
Posición espacial
Cuadriculado
Diferenciación
Repasando hasta el momento….

9.  Barras
 Líneas
 Circulares
 Histogramas
 Polígono de frecuencia
 Ojiva
 Dispersograma
 Áreas
 Cartogramas
 Pictogramas
 Pirámide poblacional
Introducción a la Estadística

10. Un gráfico de barras es aquella representación gráfica
bidimensional en que los objetos gráficos elementales son un
conjunto de rectángulos dispuestos paralelamente de manera
que la extensión de los mismos es proporcional a la magnitud
que se quiere representar.
Los rectángulos o barras pueden estar colocados horizontal o
verticalmente. En éste último caso reciben también el nombre de
gráficos de columnas
Introducción a la Estadística
Gráficos de Barras y Columna

11.  Utilización.
Típicamente se utilizan para :
 Comparar magnitudes entre varias categorías o
 La evolución en el tiempo (el cambio) de una determinada magnitud.
 La comparación de la evolución en el tiempo de varias categorías,
esto es, se suelen usar también para la mezcla de las dos utilidades
anteriores
Introducción a la Estadística

12. Introducción a la Estadística
Componentes
Un gráfico de barras consta al menos de:
Conjunto de rectángulos Un conjunto de rectángulos cuya
extensión paralela al eje cuantitativo es proporcional a la
magnitud de la categoría o secuencia representada en el eje
Eje categórico u Ordinal Un eje categórico u ordinal en el
que se disponen las categorías o los elementos de la secuencia
(el eje de abscisas [X] en un gráfico de columnas o el de
ordenadas [Y] en un gráfico de barras). Este eje es
perpendicular al cuantitativo.
Un eje cuantitativo con una escala lineal que sirve de
referencia a la magnitud de la variable en cuestión. En un
gráfico de columnas éste es el eje de ordenadas [Y] y en uno
de barras es el eje de abscisas [X]). Este eje puede contener
valores negativos

13. Introducción a la Estadística
Estratos
1986
6%
3%
24%
16%
40%
38%
30%
43%
0%
5%
10%
15%
20%
25%
30%
35%
40%
45%
Porcentaje
A/B C D E
Estratos socioeconómicos
2003
Fuente: INE. Encuesta de Hogares por Muestreo. Semestre I, 2003

14. Introducción a la Estadística
Tipos principales de gráficos de barras.
Existen muchos tipos y variantes de los mismos,
discutiremos aquí algunos de los más relevantes.
 Agrupados
Contiene varias series de datos, por ejemplo las
ventas mensuales en varios países. En este caso el
eje secuencial contendría los meses y el
cuantitativo la cifra de ventas. Cada serie de
datos se representa mediante un conjunto de
rectángulos que comparten color o textura.
 Sencillo
Contiene solamente una serie de datos (por
ejemplo, las ventas en distintos meses en un
mismo país)

15.  Apilados
También llamado segmentado o extendido, es similar al agrupado
pero cada uno de los segmentos en que está dividida la barra
pertenece a una serie de datos diferente. Muestra de qué forma
una entidad total está subdividida en partes. Si el eje no
cuantitativo es temporal permite mostrar cómo cambian estas
proporciones con el tiempo. Por ejemplo se puede hacer un gráfico
apilado con las ventas mensuales de cada país, una encima de
otra, de forma que la altura de la barra representa las ventas
totales y las proporciones de los segmentos dan idea de su
participación en el todo
Introducción a la Estadística

16. Gráficos de Líneas
 Los gráficos de líneas muestran una
serie como un conjunto de puntos
conectados mediante una línea. Los
valores se representan por el alto de
los puntos con relación al eje Y. Las
etiquetas de las categorías se
presentan en el eje X. Los gráficos
de líneas suelen utilizarse para
comparar valores a lo largo del
tiempo.
 Los gráficos de líneas son apropiados
para comparar un rasgo a lo largo del
tiempo, generalmente los usaremos
cuando tengamos una o varias series
de datos largas, con muchos puntos.
Enfatiza bien cambios en las
tendencias.
Introducción a la Estadística

17. Introducción a la Estadística
MATIAS RIUTORT IIES
-
UCAB
Pobreza e Ingreso Real de los Hogares
1975
1976
1977
1978
1979 1980
1981
1982
1983
1984
1985
1986
1987
1988
1989
1990
1991
1992
1993 1994
1995
1996
1997
1998
1975 1976
1977
1978
1979
1980
1981
1982
1983 1984
1985
1986
1987
1988
1989
1990 1991
1992
1993 1994
1995
1996
1997
1998
15
25
35
45
55
65
75
85
1975 1977 1979 1981 1983 1985 1987 1989 1991 1993 1995 1997
Años
%
0
1000
2000
3000
4000
5000
6000
7000
Bs
Pobreza
Ingreso Medio Real Hogares

18. Gráficos Circulares
En estos tipos de gráficos se
busca mostrar la tendencia de
la información generalmente en
un período de tiempo.
Pueden ser:
 Para representar una serie
 para representar dos o más
series
 en dos dimensiones
 en tres dimensiones.
Introducción a la Estadística

19. Características de los gráficos de sectores
 No muestran frecuencias acumuladas.
 Se prefiere para el tratamiento de datos
cualitativos .
 La mayor área (o porción de la figura) representa
la mayor frecuencia.
 Son muy fáciles de elaborar.
 Suelen utilizarse para representar tablas .
 La figura completa equivale al 100% de los datos
(360º).
Introducción a la Estadística

20. Gráficos Histogramas
Los histogramas de frecuencias son gráficas que
representan un conjunto de datos que se emplean
para representar datos de una variable
cuantitativa. En el eje horizontal o de las abscisas
se representan los valores tomados por la
variable, en el caso de que los valores
considerados sean continuos la forma de
representar los valores es mediante intervalos de
un mismo tamaño llamados clases. En el eje
vertical se representan los valores de las
frecuencias de los datos. Las barras que se
levantan sobre la horizontal y hasta una altura
que representa la frecuencia. Un punto
importante en el manejo de la información bajo
el uso de histogramas es el hecho de poder
comparar, bajo un proceso en control, que a
medida que se crecen las clase tiene
aproximadamente la forma de una campana
centrada, que como veremos posteriormente, es
la de una de las distribuciones mas importantes
conocidas como frecuencia normal o gaussiana.
Introducción a la Estadística

21. El polígono de frecuencias
es una representación
gráfica de la distribución
de frecuencias que resulta
esencialmente equivalente
al histograma y se obtiene
uniendo mediante
segmentos los centros de
las bases superiores de los
rectángulos del histograma
(es decir, los puntos de las
marcas de clase).
Polígono de frecuencia
Ventajas de los polígonos de frecuencias:
• Es más sencillo que su correspondiente histograma.
•Traza con más claridad el perfil del patrón de datos.

22. La ojiva es la gráfica de la frecuencia (absoluta o relativa) acumulada.
Usualmente se utiliza la frecuencia relativa expresada en términos de
porciento.
El intervalo (o el límite superior del intervalo) aparece en el eje
horizontal y la frecuencia absoluta o relativa en el eje vertical.
La ojiva indica la frecuencia acumulada en y por debajo de un intervalo
dado.
Esta gráfica facilita la comparación dos grupos de datos de forma visual y
de manera mucho más efectiva que el polígono de frecuencia, puesto
que permite comparar los porcientos acumulados de dos distribuciones
con respecto al mismo intervalo.
Se pueden emplear dos tipos de ojivas como señala Richard I. Levin, las
de “menor que” y de las de “mayor que”, como veremos en el ejemplo
siguiente.
Gráfico de la Ojiva

23.  Descendente: conocida como mayor que… donde las frecuencias
acumuladas serán el producto de la diferencia del total de la
frecuencia acumulada menos las frecuencias subsiguientes
absolutas, por lo que la primera frecuencia es el total de elementos
estudiados, Se grafican sobre los límites inferiores de cada clase.
En ambos casos pueden realizarse ojivas de frecuencias o
porcentajes.
Igualmente se grafica la clase anterior en el caso menor que, y
siguiente en el caso mayor que para partir desde una frecuencia O.
• Ascendente: conocida como ojiva menor que… Donde las
frecuencias acumuladas, se grafican considerando los limites
superiores de cada clase.

24. 0
10
20
30
40
50
60
70
249999
259999
269999
279999
289999
299999
309999
319999
Menor que…
0
10
20
30
40
50
60
70
250000
260000
270000
280000
290000
300000
310000
320000
Mayor que…

25. Gráficos Dispersogramas
Son gráficos que se construyen sobre dos ejes
ortogonales de coordenadas, llamados cartesianos,
cada punto corresponde a un par de valores de datos x
e y de un mismo elemento suceso.
Introducción a la Estadística

26. Introducción a la Estadística
Gráficos Cartogramas
Estos tipos de gráficos se utilizan para mostrar datos
sobre una base geográfica. La densidad de datos se
puede marcar por círculos, sombreado, rayado o color.

27. Gráficos Pictogramas
Los pictogramas son gráficos similares a los gráficos de barras, pero
empleando un dibujo en una determinada escala para expresar la unidad de
medida de los datos. Generalmente este dibujo debe cortarse para
representar los datos.
Es común ver gráficos de barras donde las barras se reemplazan por dibujos a
diferentes escalas con el único fin de hacer más vistoso el gráfico, estos tipos
de gráficos no constituyen un pictograma.
Pueden ser:
 En dos dimensiones
 En tres dimensiones.
Introducción a la Estadística

28. Gráficos Áreas
En estos tipos de gráficos se
busca mostrar la tendencia de
la información generalmente en
un período de tiempo.
Pueden ser:
* Para representar una serie
* Para representar dos o más
series
* En dos dimensiones
* En tres dimensiones.
Introducción a la Estadística

29. Pirámide Poblacional
 La pirámide de población es una forma gráfica de representar datos
estadísticos básicos, sexo y edad, de la población de un país, que permite
las comparaciones internacionales y una fácil y rápida percepción de
varios fenómenos demográficos tales como el envejecimiento de la
población, el equilibrio o desequilibrio entre sexos, e incluso el efecto
demográfico de catástrofes y guerras
Introducción a la Estadística

30. Errores en las gráficas
Existen varios elementos que generan una distorsión de la información
graficada, entre los más resaltantes tenemos:
 Ilusiones ópticas
 Discontinuidad en los ejes no indicada
 Ausencia de origen
 Cambios en la variable
 Intervenciones sobre los ejes
Introducción a la Estadística
Exportaciones a América Latina
85.000
98.500
63.200
85.120
98.412
96.321
14.785
85.362
15.825
25.639
75.000
88.500
53.200
75.120
88.412
86.321
4.785
75.362
5.825
25.639
0 20.000 40.000 60.000 80.000 100.000 120.000 140.000 160.000 180.000 200.000
México
Argentina
Chile
Paraguay
Colombia
Ecuador
Venezuela
Panama
Costa Rica
Perú
Países
Miles de dólares
2001
2002
Matrimonios por entidad 2003
4.920
259
5.480
1.090
50 20 34
0
1.000
2.000
3.000
4.000
5.000
6.000
D
i
s
t
r
i
t
o
C
a
p
i
t
a
l
A
m
a
z
o
n
a
s
A
n
z
o
á
t
e
g
u
i
A
p
u
r
e
A
r
a
g
u
a
B
a
r
i
n
a
s
B
o
l
í
v
a
r
Nº
de
matrimonios
Entidad