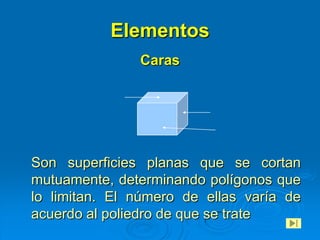
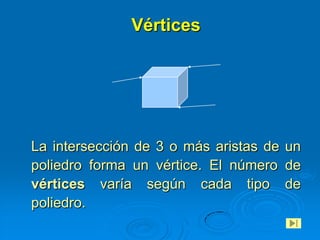
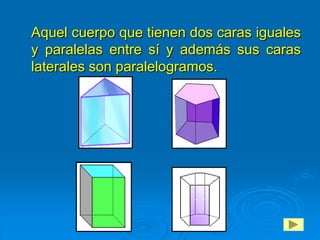
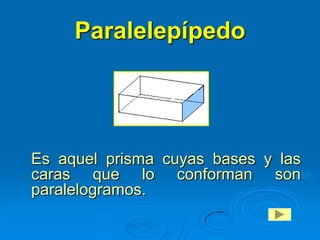
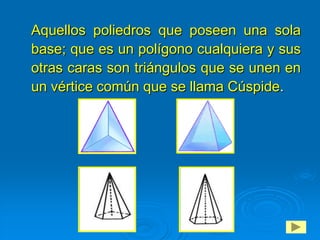
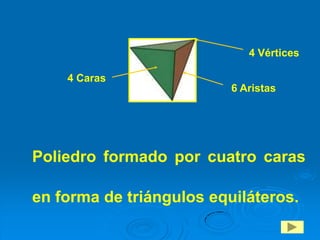
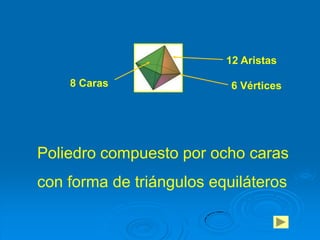
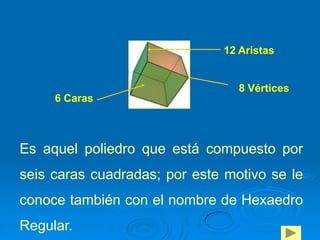
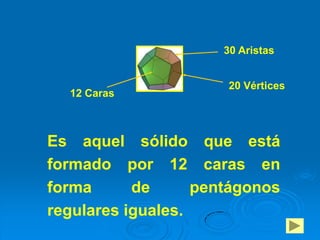
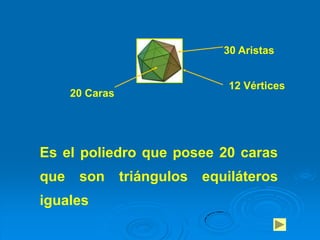
Este documento presenta un estudio sobre los poliedros para la enseñanza básica general. Define los poliedros y sus elementos principales como caras, aristas y vértices. Explica diferentes tipos de poliedros como prismas, pirámides y poliedros regulares. El objetivo es que los estudiantes reconozcan y construyan poliedros, y aprendan a calcular el área y volumen.

1. “Los buenos
florecen como
palmas y crecen
como los cedros
del Líbano”

2. ESTUDIO DE LOS
POLIEDROS PARA
LA ENSEÑANZA
BÁSICA GENERAL

3. Objetivos Generales:
 Reconocer los diferentes poliedros y cada uno de sus
elementos.
 Aplicar la técnica de construcción en el proceso de
enseñanza de los poliedros.
 Calcular el área y el volumen de los diferentes poliedros.
Objetivos Específicos:
 Definir el concepto de poliedro.
 Identificar los elementos de los diferentes poliedros.
 Construir poliedros con la utilización de diferentes
materiales.
 Resolver problemas de aplicación de área de poliedros.
 Resolver problemas de aplicación de volumen de los
diferentes poliedros.

4. Definición
Aquel sólido que está
limitado por superficies
que son polígonos

5. Elementos
Caras
Son superficies planas que se cortan
mutuamente, determinando polígonos que
lo limitan. El número de ellas varía de
acuerdo al poliedro de que se trate

6. Aristas
Son la intersección de 2 caras de un
poliedro. El número de aristas es variable
de acuerdo al poliedro del que se trate.

7. Vértices
La intersección de 3 o más aristas de un
poliedro forma un vértice. El número de
vértices varía según cada tipo de
poliedro.

8. Ángulos Poliedros
Formados por tres o más caras, con un
vértice común

9. Diagonales
Rectas trazadas entre dos vértices de
distintas caras.

10. PRISMAS
PIRÁMIDES
TRONCO DE PIRÁMIDE
POLIEDROS REGULARES

11. Aquel cuerpo que tienen dos caras iguales
y paralelas entre sí y además sus caras
laterales son paralelogramos.

12. Ejemplos de Prismas

13. Paralelepípedo
Es aquel prisma cuyas bases y las
caras que lo conforman son
paralelogramos.

14. Ejemplos de Paralelepípedos

15. Aquellos poliedros que poseen una sola
base; que es un polígono cualquiera y sus
otras caras son triángulos que se unen en
un vértice común que se llama Cúspide.

16. Ejemplos de Pirámides

17. Si una pirámide se corta por un plano
paralelo al de la base queda dividida en
dos cuerpos:
El de la parte superior es otra pirámide, y el
de la parte inferior recibe el nombre de
Tronco de Pirámide.

18. Ejemplo de Tronco de Pirámides

19. Tetraedro
Cubo
Octaedro
Dodecaedro
Icosaedro

20. 4 Vértices
4 Caras
6 Aristas
Poliedro formado por cuatro caras
en forma de triángulos equiláteros.

21. Ejemplos de Tetraedro

22. 12 Aristas
8 Caras 6 Vértices
Poliedro compuesto por ocho caras
con forma de triángulos equiláteros

23. Ejemplos de Octaedro

24. 12 Aristas
8 Vértices
6 Caras
Es aquel poliedro que está compuesto por
seis caras cuadradas; por este motivo se le
conoce también con el nombre de Hexaedro
Regular.

25. Ejemplos de Cubo

26. 30 Aristas
20 Vértices
12 Caras
Es aquel sólido que está
formado por 12 caras en
forma de pentágonos
regulares iguales.

27. Ejemplos de Dodecaedro

28. 30 Aristas
12 Vértices
20 Caras
Es el poliedro que posee 20 caras
que son triángulos equiláteros
iguales

29. Ejemplos de Icosaedro

30. CONCLUSIONES
En el proceso de enseñanza – aprendizaje de los
poliedros es fundamental la fuerza de voluntad del
docente para innovar en sus acciones educativas y
demostrar creatividad y originalidad para resolver las
dificultades metodológicas, todo ello acorde con las
necesidades educativas de los estudiantes.
La construcción de los poliedros es un elemento
clave del aprendizaje por los estudiantes, pues se
sienten productivos, ya que orientados por el docente
pueden descubrir las propiedades de los objetos o
ideas, desarrollar capacidades de análisis cuando por
sí mismo construyen y expresan sus propios
descubrimientos; y encuentran la explicación y
justificación de lo que se les expone.

31. RECOMENDACIONES
Se debe conocer de qué forma es
estructurado el espacio de forma
espontánea por los estudiantes, para que
partiendo de esa percepción, se diseñen
actividades que permitan al alumno
construir estructuras visuales geométricas
y por fin un razonamiento abstracto.
En la enseñanza de los poliedros se debe
fomentar el trabajo de los alumnos con la
ayuda de materiales manejables y que
posean el fundamento del desarrollo
lógico de la Geometría Espacial.

32. BIBLIOGRAFÍA
Cuevas, F. (2003). Matemática para la Escuela Primaria Quinto
Grado.
(11a ed.). Colombia: Imprelibros S.A..
Cuevas, F. (2000). Matemáticas 3 para la Enseñanza Básica
General.
(9a ed.). Colombia: Imprelibros S.A..
Fraile, J. & Gómez, C. (2002). Matemáticas 4. España: Graficar
Instar, S.A..
Jiménez, M. (1994). Matemática 6. San José, Costa Rica:
Editorial Satillana.
Monteverde, I. & Colamarco, A. (1976). Curso Básico Práctico de
Geometría
Plana y Sólida. Panamá: Imprenta Universidad de Panamá.
Tsijli, T. (1996). Geometría Euclídea II. San José, Costa Rica:
Editorial Universidad estatal a Distancia.
Viedna, J. Lecciones de Geometría Intuitiva. Colombia: Editorial
Mc Graw-Hill.

33. Para demostrar a Dios
el amor en la práctica,
es necesario que todas nuestras
acciones,
aún las más pequeñas,
deriven del amor hacia Dios
Gracias por la Atención
Brindada