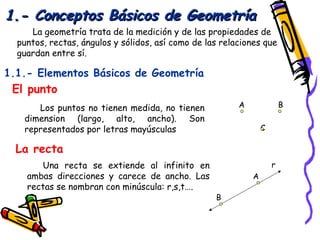
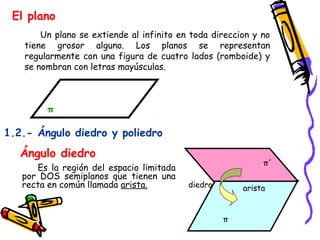
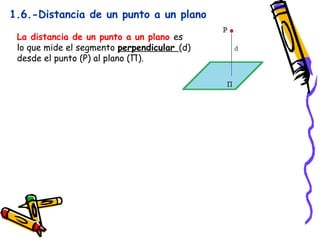
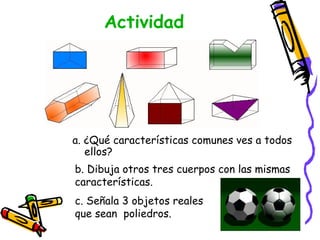
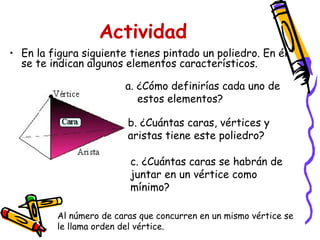
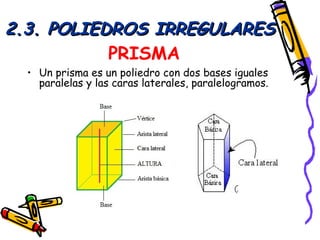
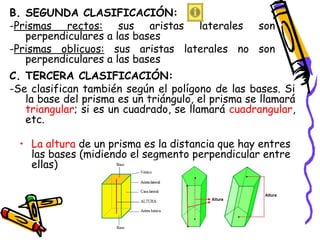
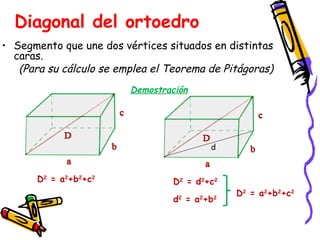
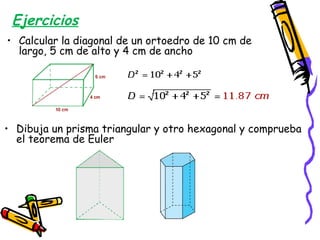
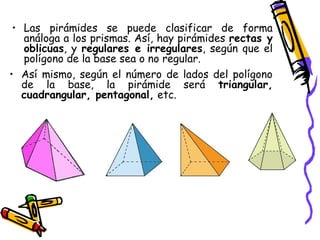
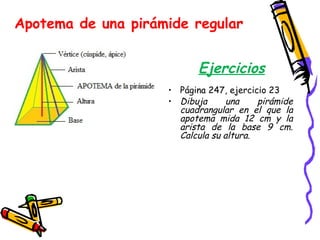
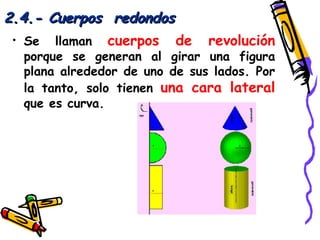
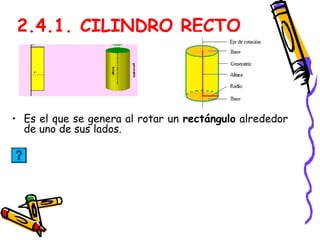
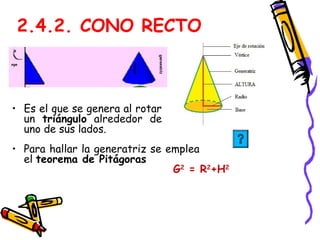
Este documento presenta conceptos básicos de geometría espacial como puntos, rectas, planos, ángulos diedros y poliedros. Explica los elementos que componen los poliedros como caras, aristas y vértices. Describe los cinco poliedros regulares (tetraedro, octaedro, icosaedro, cubo y dodecaedro) y sus características. También introduce poliedros irregulares como los prismas.

1. UNIDAD DIDÁCTICA 12:
CUERPOS EN EL ESPACIO
Matemáticas 2º ESO Fecha: 30/04/2012

2. 1.- Conceptos Básicos de Geometría
La geometría trata de la medición y de las propiedades de
puntos, rectas, ángulos y sólidos, así como de las relaciones que
guardan entre sí.
1.1.- Elementos Básicos de Geometría
El punto
Los puntos no tienen medida, no tienen A B
dimension (largo, alto, ancho). Son
representados por letras mayúsculas C
La recta
Una recta se extiende al infinito en r
ambas direcciones y carece de ancho. Las A
rectas se nombran con minúscula: r,s,t….
B

3. El plano
Un plano se extiende al infinito en toda direccion y no
tiene grosor alguno. Los planos se representan
regularmente con una figura de cuatro lados (romboide) y
se nombran con letras mayúsculas.
π
1.2.- Ángulo diedro y poliedro
Ángulo diedro
π´
Es la región del espacio limitada
por DOS semiplanos que tienen una
recta en común llamada arista. diedro arista
π

4. Ejemplo:
Una pared del aula (en
verde) y el techo (en rojo),
que confluyen en una arista
( recta) en común, forman
un ángulo diedro.
Ángulo poliedro
Es la región del espacio limitada por tres o más planos que
concurren en un punto llamado vértice.
Ejemplo:
Dos paredes adyacentes del aula (en
verde y en amarillo) y el suelo del
aula ( en rosa) forman un ángulo en el
espacio llamado triedro.

5. 1.3.-Posiciones relativas de dos rectas
a) Paralelas: Cuando están en el
mismo plano y no tienen ningún punto
en común.
b) Secantes: Cuando están en el
mismo plano y tienen un punto en
común.
c) Se cruzan: Cuando no están en el
mismo plano y no tienen ningún punto
en común.

6. 1.4.-Posiciones relativas de una recta y un plano
a) Recta contenida en el plano: Todos
los puntos de la recta están en el plano.
b) Paralelos: No tienen ningún punto
en común.
c) Secantes: La recta corta al plano
en un punto.

7. 1.5.-Posiciones relativas de dos planos
a) Paralelos: No tienen ningún punto en común.
b) Secantes: Se cortan y, por lo tanto, tienen una recta en común.

8. 1.6.-Distancia de un punto a un plano
La distancia de un punto a un plano es
lo que mide el segmento perpendicular (d)
desde el punto (P) al plano (Π).

9. 2.- Cuerpos sólidos
• Un cuerpo sólido es todo lo que ocupa
lugar en el espacio.
• Pueden ser de dos clases: o formados
por caras planas (poliedros), o
teniendo alguna o todas sus caras
curvas (cuerpos redondos).

10. Actividad
a. ¿Qué características comunes ves a todos
ellos?
b. Dibuja otros tres cuerpos con las mismas
características.
c. Señala 3 objetos reales
que sean poliedros.

11. 2.1.- Poliedros
• Estos cuerpos anteriores se
llaman poliedros.
• Son sólidos limitados por caras en
forma de polígonos.

12. Actividad
• Observa los siguientes poliedros.
• Si los sitúas en un plano, observa
que hay dos que no se pueden apoyar
sobre todas sus caras. ¿Cuáles son?

13. 2.1.1.- Clasificación de los poliedros
• Cóncavos: aquellos poliedros que
tienen alguna cara sobre la que no se
pueden apoyar.
• Convexos: se pueden apoyar sobre
todas sus caras.
(Nosotros vamos a trabajar siempre, salvo
que se indique lo contrario, con
poliedros convexos)

14. Actividad
• En la figura siguiente tienes pintado un poliedro. En él
se te indican algunos elementos característicos.
a. ¿Cómo definirías cada uno de
estos elementos?
b. ¿Cuántas caras, vértices y
aristas tiene este poliedro?
c. ¿Cuántas caras se habrán de
juntar en un vértice como
mínimo?
Al número de caras que concurren en un mismo vértice se
le llama orden del vértice.

15. 2.1.2.- Elementos de un poliedro.
Teorema de Euler
• Caras: polígonos que lo limitan
• Aristas: intersecciones de dos caras
• Vértices: puntos de intersección de
tres o mas aristas
• Al número de caras que concurren en
un mismo vértice se le llama orden del
vértice.

16. TEOREMA DE EULER
• En los poliedros
de la figura,
cuenta el
número de
caras, vértices
y aristas y
escríbelos en la
tabla.
¿Encuentras alguna relación entre C, V y A?

17. CONCLUSIÓN
• En todos los poliedros convexos se
verifica siempre que el número de
caras más el número de vértices es
igual al número de aristas más dos:
C + V = A + 2

18. Explica razonadamente cuáles de las siguientes
afirmaciones son verdaderas y cuáles son falsas
1. El número de aristas de un poliedro que
concurren en un vértice es, como mínimo, 4.
2. Las caras de un poliedro son todas iguales.
3. Hay poliedros con tres caras.
4. En cada vértice de un poliedro concurren siempre
el mismo número de aristas.
5. Las caras de un poliedro han de ser forzosamente
polígonos.
6. El número mínimo de caras que concurren
en un vértice es 3.
7. El cilindro es un poliedro.

20. 2.1.3.- Otra clasificación de Poliedros
• Regulares: aquellos poliedros todas
sus caras son regulares e iguales y
todos sus vértices son del mismo
orden.
• Irregulares: aquellos que no son
regulares.

21. 2.2. POLIEDROS REGULARES
• Se les conoce con el nombre de sólidos
platónicos en honor a Platón (siglo IV a. de
C.), pero lo cierto es que no se sabe en qué
época llegaron a conocerse. Algunos
investigadores asignan el cubo, tetraedro y
dodecaedro a Pitágoras y el octaedro e
icosaedro a Teeteto (415-369 a. de C.)

22. DEFINICIÓN
• Un poliedro es regular si todas sus
caras son regulares e iguales y
todos sus vértices son del mismo
orden.

23. 2.2.1.- Condiciones de los poliedros
a) El número mínimo de caras que
concurren en un vértice es 3 (orden
del vértice)
b) La suma de los ángulos interiores
de las caras que concurren en un
vértice deben de sumar menos de
360º.

24. 2.2.2.- Tipos de poliedros regulares
TETRAEDRO REGULAR
• Formado por cuatro triángulos equiláteros. Es el
que tiene menor volumen de los cinco en
comparación con su superficie. Representa el
fuego.
• Está formado por 4 caras, 6 aristas y 4 vértices.
• Orden del vértice: 3
• Suma de los ángulos interiores de las caras:
60º. 3 = 180º
FUEGO

25. OCTAEDRO REGULAR
• Formado por ocho triángulos equiláteros. Gira
libremente cuando se sujeta por vértices opuestos.
Por ello, representa al aire en movimiento.
• Está formado por 8 caras, 12 aristas y 6 vértices.
• Orden del vértice: 4
• Suma de los ángulos interiores de las caras:
60º. 4 = 240º
AIRE

26. ICOSAEDRO REGULAR
• Formado por veinte triángulos equiláteros. Es el
tiene mayor volumen en relación con su superficie y
representa al agua.
• Tiene 20 caras, 30 aristas y 12 vértices.
• Orden del vértice: 5
• Suma de los ángulos interiores de las caras:
60º. 5 = 300º
AGUA

27. HEXAEDRO REGULAR O
CUBO
• Formado por seis cuadrados. Permanece estable
sobre su base. Por eso representa la tierra.
• Está formado por 6 caras, 12 aristas y 8 vértices.
• Orden del vértice: 3
• Suma de los ángulos interiores de las caras:
90º. 3 = 270º
TIERRA

28. DODECAEDRO REGULAR
• Formado por doce pentágonos regulares.
Corresponde al Universo, pues sus doce caras
pueden albergar los doce signos del Zodiaco.
• Tiene 12 caras, 30 aristas y 20 vértices.
• Orden del vértice: 3
• Suma de los ángulos interiores de las caras:
108º. 3 = 324º
EL UNIVERSO

29. POLIEDROS DUALES
• Es un poliedros cuyos vértices se corresponden con
los centros de las caras de un poliedro dado.
• Se cumple que el número de caras de uno coincide
con el número de vértices del otro y viceversa

30. DESARROLLO DE
POLIEDROS
• Si en un poliedro cortamos por un
número suficiente de aristas de
forma que quede una sola pieza y la
extendemos en el plano, obtenemos
un desarrollo del poliedro.

31. Un desarrollo de cada sólido
platónico
Dibújalos en una cartulina, recórtalos y constrúyelos.

32. Poliedros en la vida cotidiana
• En adornos, en farolas, lámparas, etc.
• Los balones de fútbol han estado hechos siempre
con 12 pentágonos y 20 hexágonos (icosaedro
truncado), aunque hoy día se han cambiado por otra
forma poliédrica más redondeada (el pequeño
rombicosidodecaedro) que tiene 20 triángulos, 30
cuadrados y 12 pentágonos

33. • En sus formas naturales, muchos minerales
cristalizan formando poliedros característicos.
Cuarzo Pirita cúbica
Magnetita
• Los panales de abejas tienen forma de
prismas hexagonales
• El virus de la poliomelitis y de la
verruga tienen forma de Icosaedro

34. • En pintura, Salvador Dalí, utiliza el dodecaedro en un óleo
para enmarcar su escena sobre la última cena (con sus 12
Apóstoles). También lo utiliza en su obra Crucifixión (la
cruz se compone de 8 hexaedros adosados)

35. 2.3. POLIEDROS IRREGULARES
PRISMA
• Un prisma es un poliedro con dos bases iguales
paralelas y las caras laterales, paralelogramos.

36. 1. ¿Qué objetos reales te sugieren la idea de
prisma?
2. Si los polígonos de la base son regulares,
el prisma se llama regular.
3. ¿Incluirías los prismas regulares entre
los poliedros regulares?
A. PRIMERA CLASIFICACIÓN:
-Prismas regulares: sus bases son polígonos regulares
(todos los lados iguales)
-Prismas irregulares: sus bases nos son polígonos
regulares

37. B. SEGUNDA CLASIFICACIÓN:
-Prismas rectos: sus aristas laterales son
perpendiculares a las bases
-Prismas oblicuos: sus aristas laterales no son
perpendiculares a las bases
C. TERCERA CLASIFICACIÓN:
-Se clasifican también según el polígono de las bases. Si
la base del prisma es un triángulo, el prisma se llamará
triangular; si es un cuadrado, se llamará cuadrangular,
etc.
• La altura de un prisma es la distancia que hay entres
las bases (midiendo el segmento perpendicular entre
ellas)

39. Prismas interesantes:
Paralelepípedos
• Prismas cuyas 2 bases y 4 caras son paralelogramos
(polígono de 4 lados)
• Si además es recto, y sus seis caras son rectángulos,
se llama ortoedro.

40. Diagonal del ortoedro
• Segmento que une dos vértices situados en distintas
caras.
(Para su cálculo se emplea el Teorema de Pitágoras)
Demostración
d
D2 = a2+b2+c2 D2 = d2+c2
D2 = a2+b2+c2
d2 = a2+b2

41. Ejercicios
• Calcular la diagonal de un ortoedro de 10 cm de
largo, 5 cm de alto y 4 cm de ancho
• Dibuja un prisma triangular y otro hexagonal y comprueba
el teorema de Euler

42. PIRÁMIDE
• Una pirámide es un poliedro cuya base es un
polígono y sus caras laterales son triángulos que
concurren en el vértice de la pirámide.

43. • Las pirámides se puede clasificar de forma
análoga a los prismas. Así, hay pirámides rectas y
oblicuas, y regulares e irregulares, según que el
polígono de la base sea o no regular.
• Así mismo, según el número de lados del polígono
de la base, la pirámide será triangular,
cuadrangular, pentagonal, etc.

44. Apotema de una pirámide regular
Ejercicios
• Página 247, ejercicio 23
• Dibuja una pirámide
cuadrangular en el que la
apotema mida 12 cm y la
arista de la base 9 cm.
Calcula su altura.

45. TRONCO DE PIRÁMIDE
• Es el poliedro que se obtiene al cortar una
pirámide regular por un plano paralelo a la base.
• Las caras laterales de un tronco de
pirámide son trapecios isósceles
iguales y su altura coincide con la
apotema del tronco de pirámide.
• Página 247, ejercicio 25

47. 2.4.- Cuerpos redondos
• Se llaman cuerpos de revolución
porque se generan al girar una figura
plana alrededor de uno de sus lados. Por
la tanto, solo tienen una cara lateral
que es curva.

48. 2.4.1. CILINDRO RECTO
• Es el que se genera al rotar un rectángulo alrededor
de uno de sus lados.

49. 2.4.2. CONO RECTO
• Es el que se genera al rotar
un triángulo alrededor de
uno de sus lados.
• Para hallar la generatriz se emplea
el teorema de Pitágoras
G2 = R2+H2

50. 2.4.3. ESFERA
• Es el que se genera al rotar un semicírculo sobre su
diámetro.