Los sólidos platónicos son los únicos poliedros que tienen caras regulares iguales y en los que el mismo número de caras se unen en cada vértice. Los cinco sólidos platónicos son el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro. Cada sólido platónico tiene propiedades únicas de simetría y regularidad.

1. Sólidos platónicos
De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
Los sólidos platónicos son poliedros convexos cuyas caras son polígonos regulares iguales
y en cuyos vértices se unen el mismo número de caras. Reciben este nombre en honor al
filósofo griego Platón (ca. 427 adC/428 adC – 347 adC), a quien se atribuye haberlos
estudiado en primera instancia. También se conocen como cuerpos platónicos, cuerpos
cósmicos, sólidos pitagóricos, sólidos perfectos, poliedros de Platón o, con más
precisión, poliedros regulares convexos.
Los sólidos platónicos son el tetraedro, el cubo (o hexaedro regular), el octaedro, el
dodecaedro y el icosaedro. Esta lista es exhaustiva, ya que es imposible construir otro
sólido diferente de los anteriores que cumpla todas las propiedades exigidas, es decir,
convexidad y regularidad.
[editar] Propiedades
[editar] Regularidad
Tal y como se ha expresado para definir estos poliedros:
Todas las caras de un sólido platónico son polígonos regulares iguales.
En todos los vértices de un sólido platónico concurren el mismo número de caras y
de vértices.
Todas las aristas de un sólido platónico tienen la misma longitud.
Todos los ángulos diedros que forman las caras de un sólido platónico entre sí son
iguales.
Todos sus vertices son convexos a los del icosaedro.
[editar] Simetría
Los sólidos platónicos son fuertemente simétricos:
Todos ellos gozan de simetría central respecto a un punto del espacio (centro de
simetría) que equidista de sus caras, de sus vértices y de sus aristas.
Todos ellos tienen además simetría axial respecto a una serie de ejes de simetría que
pasan por el centro de simetría anterior.
Todos ellos tienen también simetría especular respecto a una serie de planos de
simetría (o planos principales), que los dividen en dos partes iguales.

2. Como consecuencia geométrica de lo anterior, se pueden trazar en todo sólido platónico
tres esferas particulares, todas ellas centradas en el centro de simetría del poliedro:
Una esfera inscrita, tangente a todas sus caras en su centro.
Una segunda esfera tangente a todas las aristas en su centro.
Una esfera circunscrita, que pase por todos los vértices del poliedro.
Proyectando los centros de las aristas de un poliedro platónico sobre su esfera circunscrita
desde el centro de simetría del poliedro se obtiene una red esférica regular, compuesta por
arcos iguales de círculo máximo, que constituyen polígonos esféricos regulares.
[editar] Conjugación
Artículo principal: Poliedro dual.
Si se traza un poliedro empleando como vértices los centros de las caras de un sólido
platónico se obtiene otro sólido platónico, llamado conjugado del primero, con tantos
vértices como caras tenía el sólido inicial, y el mismo número de aristas. El poliedro
conjugado de un dodecaedro es un icosaedro, y viceversa; el de un cubo es un octaedro; y
poliedro conjugado de un tetraedro es otro tetraedro.
[editar] Esquema
El Teorema de poliedros de Euler fija que el número de caras de un poliedro platónico más
su número de vértices es siempre igual a su número de aristas más dos, es decir:
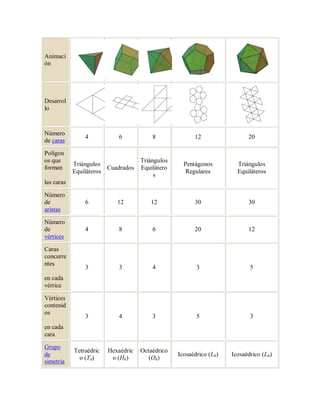
[editar] Tabla comparativa
Hexaedro,
Tetraedro Octaedro Dodecaedro Icosaedro
Cubo
Sólidos
Platónic
os

3. Animaci
ón
Desarrol
lo
Número
4 6 8 12 20
de caras
Polígon
os que Triángulos
Triángulos Pentágonos Triángulos
forman Cuadrados Equilátero
Equiláteros Regulares Equiláteros
s
las caras
Número
de 6 12 12 30 30
aristas
Número
de 4 8 6 20 12
vértices
Caras
concurre
ntes
3 3 4 3 5
en cada
vértice
Vértices
contenid
os
3 4 3 5 3
en cada
cara
Grupo
Tetraédric Hexaédric Octaédrico
de Icosaédrico (Lh) Icosaédrico (Lh)
o (Td) o (Hh) (Oh)
simetría

4. Poliedro Tetraedro
Hexaedro,
conjuga (autoconju Octaedro Icosaedro Dodecaedro
Cubo
do gado)
Símbolo
de {3,3} {4,3} {3,4} {5,3} {3,5}
Schläfli
Símbolo
de 3|23 3|24 4|23 3|25 5|23
Wythoff
109.47° =
Ángulo 70.53° =
90° arccos(- 116.56° 138.189685°
diedro arccos(1/3)
1/3)
Radio
externo
Radio
interno
[editar] Poliedros regulares en la naturaleza
En la naturaleza hay estructuras que son poliedros regulares casi perfectos, por ejemplo, la
estructura básica del VIH es un icosaedro regular[cita