Incrustar presentación
Descargar para leer sin conexión









![Conjeturas con primos
• La conjetura de Goldbach: todo número par
puede expresarse como la suma de dos
números primos.
• La conjetura de los primos gemelos: existen
infinitos números primos gemelos [si p y p + 2
son números primos se dicen que son gemelos]
• La conjetura de Legendre: siempre existe un
número primo entre n2 y (n + 1)2](https://image.slidesharecdn.com/numeros-160223095813/85/Primos-11-320.jpg)

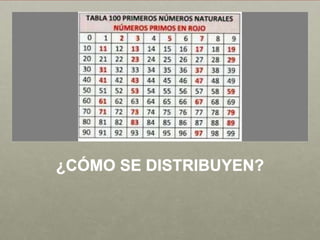
El documento habla sobre números primos y su distribución. Menciona a matemáticos como Euclides, Gauss y Riemann, cuyos trabajos ayudaron a comprender y estimar la abundancia de números primos. También discute conjeturas sin resolver sobre números primos como la conjetura de Goldbach y la conjetura de los primos gemelos.










![Conjeturas con primos
• La conjetura de Goldbach: todo número par
puede expresarse como la suma de dos
números primos.
• La conjetura de los primos gemelos: existen
infinitos números primos gemelos [si p y p + 2
son números primos se dicen que son gemelos]
• La conjetura de Legendre: siempre existe un
número primo entre n2 y (n + 1)2](https://image.slidesharecdn.com/numeros-160223095813/85/Primos-11-320.jpg)
