Capítulo 4. Derivada y aplicaciones

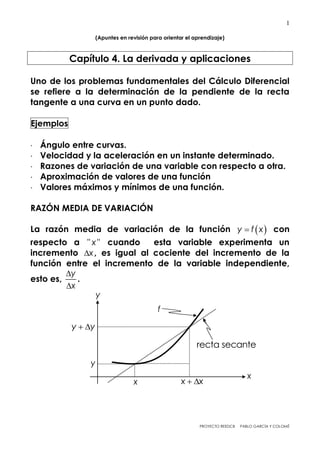
1
PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ
(Apuntes en revisión para orientar el aprendizaje)
Capítulo 4. La derivada y aplicaciones
Uno de los problemas fundamentales del Cálculo Diferencial
se refiere a la determinación de la pendiente de la recta
tangente a una curva en un punto dado.
Ejemplos
 Ángulo entre curvas.
 Velocidad y la aceleración en un instante determinado.
 Razones de variación de una variable con respecto a otra.
 Aproximación de valores de una función
 Valores máximos y mínimos de una función.
RAZÓN MEDIA DE VARIACIÓN
La razón media de variación de la función  y f x con
respecto a " "x cuando esta variable experimenta un
incremento x , es igual al cociente del incremento de la
función entre el incremento de la variable independiente,
esto es,
y
x


.
y
x
y y 
y
f
x x x 
recta secante

ING. PABLO GARCÍA Y COLOMÉ
2
CONCEPTO DE RECTA TANGENTE
Pierre de Fermat (1601-1665). Jurista, matemático y físico
LA DERIVADA COMO RAZÓN INSTANTÁNEA DE VARIACIÓN
Definición. A la razón instantánea de variación de una
función f con respecto a " "x , se le conoce como la derivada
de la función con respecto a la variable independiente, es
decir,
0
lim derivada de con respecto a " "
x
y
f x
x 



De acuerdo con lo ya tratado, se puede escribir que:
   0 0
0
lim ;
x
dy y
y f x x f x
dx x 

     

f
B
A
recta secante
x
recta tangente
 lim secante tangente
B A

y
x
y
m
x



 f x x 
 f x
y mx b 
x x x 
y
x
y

3
   0 0
0
lim
x
f x x f xdy
dx x 
  


y si además se considera que 0x x x   , entonces
   
0
0
0
0
0 lim
x x
f x f xdy
x x x
dx x x

     

Esta expresión define a la derivada de la función,
específicamente en el punto en el que 0x x .
INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA
 lim recta secante recta tangente
B A

0 0
0 ; lim lim tan tan
x x
B A x    
   
      
0
tan BAC=tan = lim tan
x
y y dy
x x dx
 
 
 
  
 
tan T
dy
m
dx
 
Notaciones
 ' ' notación de Lagrangey ó f x
  notación de Cauchyx xD y ó D f x
  notación de Leibniz
dy d
ó f x
dx dx
  notación de Newtony ó f x
y
x x x 
 f x
 f x x 
f
y
x
A
x
B
 
C
secante
tangente

4
Ejemplo. Supóngase que parte de la trayectoria de un juego
mecánico de montaña rusa tiene la forma mostrada en la
figura, donde el recorrido de A a B y de B a C, son curvas
parabólicas distintas, y el recorrido de C a D es una media
circunferencia.
Si se denota con " " el ángulo que forma el piso del carrito
con la línea horizontal:
)i ¿Qué valor tiene  en el punto más alto?
)ii ¿Qué valor tiene  en el punto más bajo?
)iii ¿Existen otros puntos en donde tenga el mismo valor que
los que tuvo en los primeros incisos?
Ejemplo. Se tiene una pila de cemento colocada junto a una
pared vertical sobre un piso horizontal. Considerando el
origen de coordenadas en la intersección de piso y pared, el
perfil del cemento está descrito, con una buena
aproximación, por la curva 2
9y x   . Supóngase además
que hay una escalera perfectamente recta e indeformable
que se apoya simultáneamente en la pared, el cemento y el
suelo.
)i Demostrar que si la abscisa del punto de contacto de la
escalera con la pila de cemento es 1.5, entonces la
ecuación de la escalera se puede expresar como
3 11.25y x   .
)ii Determinar la longitud de la escalera.
A B C D

5
Ejemplo. Determinar la ecuación de la recta que pasa por el
punto  4,0 y es tangente a la curva 1y x   . Obtener
también las coordenadas del punto de tangencia y hacer un
dibujo del problema planteado.

6
Ejemplo. El volumen de un cierto tipo de bacterias en un
cultivo de laboratorio es inversamente proporcional al
número de días " "n que pasan sin nutrientes, de tal forma
que el modelo para esta relación es:
10,000
V
n

función que se satisface a partir del primer día, es decir,
cuando 1n  y 10,000V  bacterias. Obtener la razón de
cambio en la que decrece el número de bacterias con
respecto a los días sin alimento, cuando 4n  .
Ejemplo. El costo de una cierta aleación de metales
depende de la cantidad de oro que contiene. La mínima
cantidad que debe contener es de 3 gramos y su costo es
de $ 81,000 y aumenta este de acuerdo con el modelo:
3 2
5000 6000C x x 
donde " "C es el costo en pesos y " "x el oro en gramos.
Determinar la razón de cambio del costo de la aleación, con
respecto a la cantidad de oro, cuando tiene "5" gramos de
este metal precioso.

7
Derivación a través de la definición
Ejemplo. Calcular la derivada de las siguientes funciones
mediante la definición, que comúnmente se conoce como
método de los cuatro pasos:
3 3
) 6 1 ; ) ; ) 5 2
5
x
i y x x ii y iii y x
x

     


8
Teorema. Derivada de la función constante
Sea la función constante   , con una constantey f x k k  .
Entonces su derivada es igual a cero, es decir, 0
dy
dx
 .
 0 0
; lim lim 0 0
x x
dy k k dy dy
y k
dx x dx dx   

     

Teorema. Derivada de la función identidad.
Sea la función identidad  y f x x  . Entonces su derivada es
igual a la unidad, esto es,
1
dy
dx

x
k
y
0T
dy
m
dx
 
y k

9
 0 0
; lim lim 1 1
x x
dy x x x dy dy
y x
dx x dx dx   
  
     

Teorema. Derivada de la función identidad elevada a un
exponente real. Aquí sólo se verá el caso del exponente
natural. Elevada a un exponente real también es
demostrable. Sea entonces la función ;n
y x n  .
Entonces su derivada está dada por:
1ndy
nx
dx


Prueba.
 
0
lim
n n
x
x x xdy
dx x 
  


A través del desarrollo del binomio de Newton, se llega a:
  2
1 2
0
1
1! 2!lim
n
n n n n
x
n nn
x x x x x x x
dy
dx x
 
 

       


  1
1 2
0
1
lim
1! 2!
n
n n
x
n ndy n
x x x x
dx

 
 
 
      
 
1ndy
nx
dx


Ejemplo. Calcular la derivada de las funciones siguientes:
  5
) ; ) 4i f x x ii y 
x
y
y x
0
45
1T
dy
m
dx
 

10
Teorema. Derivada de la suma de funciones.
Considérese la función      h x f x g x  . Entonces, la
derivada de la función " "h es igual a:
     ' ' 'h x f x g x 
Teorema. Derivada del producto de una función por un
escalar.
Sea la función     ;h x f x   . Entonces su derivada
será:
   ' 'h x f x

11
Ejemplo. Obtener la derivada de la función:
   
1
6 4 2 2
2
2 1
) 5 ; ) 3 2 7 ; ) 8
3
i f x x ii f x x x x iii y x
xx
       
Teorema. Derivada de una función como radicando de una
raíz cuadrada. Sea la función    h x f x . Entonces su
derivada es igual a:
 
 
 
'
'
2
f x
h x
f x


12
Ejemplo. Obtener la derivada de la función
1
3
3 5y x 
Teorema. Derivada del producto de dos funciones
Sea la función      h x f x g x  . Entonces, la derivada de " "h
es:
         ' ' 'h x f x g x g x f x   

13
Ejemplo. Obtener la derivada de:
   3 2 2
3 1f x x x x  
Teorema. Derivada de un cociente de funciones.
Sea la función " "h dada por  
 
 
f x
h x
g x
 , esto es, cuya regla
de correspondencia involucra el cociente de las funciones
" "f y " "g . Entonces su derivada es igual a:
 
       
 
2
' '
'
g x f x f x g x
h x
g x
  

  

14
Ejemplo. Derivar las siguientes funciones:
 
2 2 3
2
3 6 2
) ; )
1 5 6
x x x
i f x ii y
x x x

 
 
  
Teorema. Regla de la cadena (Derivada de una función de
función).
Sean las funciones  y f u y  u g x , ambas derivables,
tales que con ellas se logra la función compuesta
     ;g fy f g x x x x D g x D    
Entonces se cumple que:
dy dy du
dx du dx

Ejemplo. Obtener la derivada de la función
   
3
2 2
2
23
2
1
) ; ) ; ) 3 1 2
11
x x
i y ii f x iii y x
xx
 
      
 

15
Ejemplo. Calcular las derivadas de las funciones siguientes y
evaluarlas en el punto indicado.
 
 
2 2
3
3
8 3 9
) ; 1 ; ) ; 1
5
x x
i y x ii f x x
xx
 
    


16
Resumen de las fórmulas obtenidas:
Sean , ,u v w funciones de " "x y " "C una constante real:
Entonces:
0xD C  1xD x 
 x x x xD u v w D u D v D w      x x xD uv uD v vD u 
x xD Cv CD v 2
x x
x
vD u uD vu
D
v v


2
x
x
CD vC
D
v v
  1n n
x xD u nu D u

1n n
xD x nx 

2
x
x
D u
D u
u

DERIVADA DE FUNCIONES EXPRESADAS EN FORMA IMPLÍCITA
Ejemplo. Calcular
dy
dx
en las ecuaciones:
2 2 4 2 3
4 ; )2 8 4x y ii x y xy y y    

17
Ejemplo. Considérese la ecuación 4 18
y x
x y
  .
Demostrar que
dy y
dx x
 .
DERIVADA DE LAS FUNCIONES CIRCULARES DIRECTAS
Teorema.  ; cos
dy du
y senu u f x u
dx dx
   

18
Teorema.  cos ;
dy du
y u u f x senu
dx dx
    
Teorema.   2
tan ; sec
dy du
y u u f x u
dx dx
   
Teorema.   2
cot ; csc
dy du
y u u f x u
dx dx
    
Teorema.  sec ; sec tan
dy du
y u u f x u u
dx dx
   
Teorema.  csc ; csc cot
dy du
y u u f x u u
dx dx
    

19
Ejemplo. Derivar las siguientes funciones:
     21 cos
) ; ) 1 5 ; ) tan
1 cos
x
i f x ii y sen x iii f x x
x

   

   2 2 31
) sec csc ; ) cotiv y x v f x senx
x
  
 
1
2 3
) sec 2 6vi y x 

20

21
DERIVADA DE LAS FUNCIONES CIRCULARES INVERSAS
Teorema.   2
;
1
du
dy dxy angsenu u f x
dx u
   

Teorema.   2
cos ;
1
du
dy dxy ang u u f x
dx u
    

Teorema.   2
tan ;
1
du
dy dxy ang u u f x
dx u
   

Teorema.   2
cot ;
1
du
dy dxy ang u u f x
dx u
    


22
Teorema.   2
sec ;
1
du
dy dxy ang u u f x
dx u u
   

Teorema.   2
csc ;
1
du
dy dxy ang u u f x
dx u u
    

Ejemplo. Calcular la derivada de las siguientes funciones:
  2
) se 1 ; ) seci f x ang n x ii y ang x  
   2
) cot ; ) cos 1iii f x x ang x iv y ang x  
   21
) tan ; ) csc 8v f x x ang vi y ang x
x
  

23
Resumen de las fórmulas para derivar funciones circulares
directas e inversas:
Sea  u f x . Entonces:
cosx
du
D senu u
dx

2
1
x
x
D u
D angsenu
u


cos
du
D u senu
x dx
 
2
cos
1
x
x
D u
D ang u
u
 

2
tan secx
du
D u u
dx
 2
tan
1
x
x
D u
D ang u
u


2
cot cscx
du
D u u
dx
  cot
21
x
x
D u
D u
u
 

sec sec tanx
du
D u u u
dx

2
sec
1
x
x
D u
D u
u u


csc csc cot
du
D u u u
x dx
 
2
1
x
x
D u
D u
u u
 


24
DERIVADA DE UNA FUNCIÓN DEFINIDA EN FORMA
PARAMÉTRICA
 
 
 
 
'
: ; ,
'
dy
x f t g tdy dydtf t a b
dxdx dx f ty g t
dt
 
       

Ejemplo. Dadas las siguientes funciones, obtener la derivada
dy
dx
.
 
 
2
22
) : ; 0 ; ) ;
2 1 cos1
cot 1
) : ; 1 1
tan 1
x senx t t
i f t ii
yy t
x ang t
iii f t
y ang t
 


     
  
     
  
  
 

25
DERIVADAS DE ÓRDENES SUPERIORES
     
 
2
2
3
3
; ' ' ; '' ''
''' ''' ;
dy d y
y f x y f x y f x
dx dx
d y
y f x
dx
    
 
       
1 2 5 8
3 3 3 3
1 2 10
; ' ; '' ; '''
3 9 27
f x x f x x f x x f x x
  
    
2 3
2 3
; cos ; ; cos
dy d y d y
y senx x senx x
dx dx dx
     
x
y
x
x
x
3
3
x
y 
3
3
2
d y
dx

2dy
x
dx

2
2
2
d y
x
dx


26
Ejemplo. Obtener las dos primeras derivadas de la siguiente
función y evaluarlas para 2x  .
2
x
y
x


DERIVADA DE LAS FUNCIONES LOGARÍTMICA, EXPONENCIAL E
HIPERBÓLICAS
TEOREMA. Sea la función logaritmo natural
   ln ;f x u u g x 
 
1
'
du
du dxf x
u dx u
 
Prueba. Se aplicará la definición de derivada.
   ln ln ln lny u y y u u y u u u            
 ln lnu u uy
u u
  

 
Por propiedades de la función logaritmo natural,
 
ln 1 ln 1lnln ln
u uu u
u u uy uu uu
u u u u u u
                   
    

27
1 1
ln 1 ln 1
u
uy u u u
u u u u u u
     
           
0 0 0 0
1 1
lim lim ln 1 lim lim 1
u u
u u
u u u u
y u u
u u u u u
 
       
     
           
0 0
1 1
lim ; lim 1 1
u
u
u u
u
u u u

   
 
   
 
 0
1 1
lim 1
u
y dy
u du u u 

  

Finalmente se aplica la regla de la cadena y:
 
1
'
du
dy du dxf x
dx u dx u
  
Es evidente que:
   
  1dLn x
f x Ln x
dx x
  
TEOREMA. Sea la función exponencial
   ;u
f x e u g x 
 ' u du
f x e
dx

Prueba.
 ; ln ln lnu u
y e u g x y e y u     
y si se deriva en forma implícita con respecto a " "u se tiene:
 1
' 1 ; ' u u
y y y D e e
y
   
Y, mediante la regla de la cadena, se llega finalmente a:
 u u ud du
D e e e
dx dx
 
Es evidente que:
   'x x
f x e f x e  

28
Ahora se verán las fórmulas de derivación para funciones
logarítmicas y exponenciales con una base cualquiera " "b .
Antes se presentarán dos formas equivalentes para obtener
el valor de la función logaritmo base " "b en términos del
valor de la función logaritmo natural:
ln
ln log logu w w
b bu w e e u e u w e      
log ln logb bu u e 
        log
log ln ln ln log lnb u v v
b bu v b b u b u v b u u b
ln
log
ln
b
u
u
b
 
TEOREMA. Sea la función logarítmica con una base
cualquiera base " "b , es decir,
   log ; ; 0 ; 1by u u f x b b    .
Entonces, su derivada es:
logb
du
dy dx e
dx u
 o bien
ln
du
dy dx
dx u b

Prueba. La función   log ;by u u f x también puede
expresarse, como ya se vio, en términos del logaritmo natural
de " "u como:
 ln log ; logb b
du
dy dxy u e u f x e
dx u
   
Se sabe también que esta función se puede expresar en
términos de la función logaritmo natural como:
 
ln
log ;
ln lnb
du
u dy dxy u u f x y
b dx u b
     

29
Ahora se obtendrá la derivada de la función exponencial
con una base cualquiera  " " ; 0 ; 1b b b  :
TEOREMA. Sea la función
 ;u
y b u f x 
donde " "b es un valor real positivo cualquiera y diferente de
la unidad. Entonces su derivada es:
lnudy du
b b
dx dx

Prueba. Se aplica la función logaritmo natural y,
 ; ln lnu
y b u f x y u b   
Se deriva la expresión obtenida de manera implícita y,
ln ln lnu
dy
du dy du dy dudx b y b b b
y dx dx dx dx dx
    
TEOREMA. Sea la función:
 
 
;v
u f x
y u
v g x



Entonces su derivada es:
1
lnv vdy du dv
vu u u
dx dx dx

 
Prueba. Se aplica la función logaritmo natural y se deriva de
manera implícita:
ln ln ln
dy du
dvdx dxy v u v u
y u dx
   
1
ln lnv v v
du
dy dv dy du dvdxu v u vu u u
dx u dx dx dx dx

 
 
      
 
 

30
Ejemplo. Obtener la derivada de tanx
y x .
Ejemplo. Calcular las siguientes derivadas:
   
2
2 2 11 cos
) ln ; ) logsec 1 ; )
1 cos
xx
i y ii f x x iii y e
x

   

   
 
2 3
cos 2 cos 1
) 10 ; ) ; ) ln
2
x x senx
iv f x v y senx vi y
senx
  
  


31

32
Derivadas de las funciones hiperbólicas directas e inversas
Obtener las expresiones para derivar estas funciones resulta
sencillo ya que las directas están en términos de la función
exponencial y las inversas en términos de la función logaritmo
natural, cuyas derivadas se conocen. Por eso solamente se
desarrollarán las de la función senhx así como la de su
inversa.
   ;f x senhu u g x 
cosh
2 2
u u u u
e e dy e e
y senhu u
du
 
 
    
Y por la regla de la cadena
 ' cosh
du
f x u
dx

     cosh ; '
du
f x u u g x f x senhu
dx
   
      2
tanh ; ' sec
du
f x u u g x f x h u
dx
   
      2
coth ; ' csc
du
f x u u g x f x h u
dx
    
     sech ; ' sec tanh
du
f x u u g x f x hu u
dx
    
     csch ; ' csc coth
du
f x u u g x f x hu u
dx
    
   1
;f x senh u u g x
 
 1 2
ln 1y senh u u u
   

33
2
2 2
2 2 2
1
1
11 1
1 1 1
u u u
dy u u
du u u u u u
 

    
    
  2 2
1
'
u 1 u 1
du
du dxf x
dx
  
 
     1
2 2
1
cosh ; ' ; 1
1 1
du
du dxf x u u g x f x u
dxu u

     
 
     1
2 2
1
tanh ; ' ; 1
1 1
du
dxu u

     
 
     1
2 2
1
coth ; ' ; 1
1 1
du
dxu u

     
 
     1
2 2
1
sech ; ' ; 0 1
1 1
du
dxu u u u
 
       
 
     1
2 2
1
csch ; ' ; 0
1 1
du
dxu u u u
 
      
 
Ejemplo. Obtener las derivadas de las siguientes funciones:
   2 2
) ( ) senh 1 2 ; ) ( ) cosh lni f x x ii f x x  
    cosh
) cot senh3 ; ) senh x
iii y ang x iv y x e 
2
cosh
) ; ) ln tanh
24 senh
x x
v y vi y
x
  
       
  coth
) tan tanh ; ) ( ) x
vii y ang x viii f x x 

34
 
1 1
) ln sec 4 ; ) ( ) ln sec ln cscix y x h x x f x h h
x x
   
     
   
Solución.
 2 2
) ( ) senh 1 2i f x x 
     2 2
'( ) 2senh 1 2 cosh 1 2 4f x x x x    
   2
' 4 senh 2 4f x x x   
 ) ( ) cosh lnii f x x
 
1
2'( ) senh ln xf x x
x
 
   1
' senh ln
2
f x x
x
 
 ) cot senh3iii y ang x
2 2
3cosh3 3cosh3 3
cosh31 senh 3 cosh 3
dy x x
dx xx x

    

3sec 3
dy
h x
dx
  
  cosh
) senh x
iv y x e
    cosh cosh
senh senh coshx xdy
x x e x e
dx
 
 cosh 2
senh coshxdy
e x x
dx
  
2
cosh
)
4 senh
x
v y
x


   
 
2
2
2
4 senh senh cosh 2senh cosh
4 senh
x x x x xdy
dx x
 



35
 
 
2 2
2
2
senh 4 senh 2cosh
4 senh
x x xdy
dx x
 


 
 
2 2 2
2
2
senh 4 cosh cosh senh
4 senh
x x x xdy
dx x
   
 

 
 
2
2
2
senh 3 cosh
4 senh
x xdy
dx x

 

) ln tanh
2
x
vi y
  
   
  
 
22
2
1
1 coshsec 1 122
tanh senh 2senh cosh senh2
2 2 2 2 2
2
cosh
2
x
x
hdy
x x x x xdx
x
 
 
    
         
         
         
 
 
 
csc
dy
hx
dx
 
 ) tan tanhvii y ang x
2 2
2 22 2 2
2
1
sec 1 1cosh
cosh senh1 tanh cosh senh cosh2
cosh
dy h x x
x xdx x x x x
x
   
 
sec 2
dy
h x
dx
 
coth
) ( ) x
viii f x x
   coth 1 coth 2
'( ) coth ln cscx x
f x x x x x h x
  
   coth 2coth
' ln cscx x
f x x x h x
x
 
   
 

36
 ) ln sec 4ix y x h x
 
4sec 4 tanh4
ln sec 4
sec 4
dy h x x
x h x
dx h x

  
 4 tanh4 ln sec 4
dy
x x h x
dx
   
1 1
) ( ) ln sec ln cscx f x h h
x x
   
    
   
2 2
1 1 1 1 1 1
sec tanh csc coth
'( )
1 1
sec csc
h h
x x x xx x
f x
h h
x x
   
      
    
2 2
1 1
tanh coth
x x
x x
 
2 2
2
2 2
1 1
senh cosh
1 1 1 1 2
cosh senh senh cosh 2cosh
2
'( )
1 1 22
senh cosh senh
x x
x x x x xf x
x
x x
x x x


   
  2
2 2
' cothf x
xx
 
Ejemplo. Obtener la derivada de las siguientes funciones:
1 1 2
) senh ; ) ( ) senh 4
2
x
i y x x ii f x x x   
    
 
 1 2 1
) cosh ; ) tanh cosiii y x iv y x 
 
1 2 1 2
) ( ) tanh ln 1 ; ) coth 1v f x x x x vi y x 
    
   1 1
) coth sen2 ; ) ( ) sec cos2vii y x viii f x h x 
 
 1 1 1
) ( ) csc tan ; ) tan tanhix f x h x x y x  
 
Solución.
1
) senhi y x x


37
1
1
12 senh
1 2
dy xx x
dx x x

  

11 1
senh
2 1 2
dy
x
dx x x

  

1 2
) ( ) senh 4
2
x
ii f x x x  
   
 
1
2 2
1
2'( ) senh
2 4
1
4
x x
f x x
x x
  
    
  

1
2 2
senh
24 4
x x x
x x
  
   
  
  1
' senh
2
x
f x   
   
 
1 2
) coshiii y x

4
2
1
dy x
dx x
 

 1
) tanh cosiv y x

2 2
sen sen
1 cos sen
dy x x
dx x x
 
 

csc
dy
x
dx
  
1 2
) ( ) tanh ln 1v f x x x x
  
2
1
2 2
1 1'( ) tanh
1 1
x
xf x x x
x x


   
 
1
2 2
tanh
1 1
x x
x
x x

  
 

38
  1
' tanhf x x
 
1 2
) coth 1vi y x
 
 
2
2
1
1 1
x
dy x
dx x

 
2
1
1
dy
dx x x
  

 1
) coth sen2vii y x

2
2cos2 2
cos21 sen 2
dy x
dx xx
 

2sec2
dy
x
dx
 
 1
) ( ) sec cos2viii f x h x

 
2
2sen2 2sen2 2
'( )
cos2 sen2 cos2cos2 1 cos 2
x x
f x
x x xx x
 
  

 ' 2sec2f x x 
 1
) ( ) csc tanix f x h x

2 2
2
1
sec sec cos'( )
sentan sectan 1 tan
cos
x x xf x
xx xx x
x

 
  

 ' cscf x x  
1 1
) tan tanhx y x 

2 2
1
1 1
dy
dx
y x

 

39
 
2
1
2
2 2
1 tan tanh1
1 1
xdy y dy
dx dxx x
      
 
DERIVADAS DE ORDEN SUPERIOR PARA FUNCIONES IMPLÍCITAS
Y PARA FUNCIONES REPRESENTADAS EN FORMA PARAMÉTRICA
 
 
1
12
2
: ;
n
nn
n
d d yd dy
x f t dt dxd y d ydt dx
f
dx dxdx dxy g t
dt dt


  
         

Ejemplo. Calcular la primera y segunda derivadas de:
2 2
) 1 ; ) 2 5i x y ii x xy y    

40
Ejemplo. Obtener las tres primeras derivadas para:
5cos
: ; 0 2
3
x
f
y sen

 


 

Ejemplo. Ecuación cartesiana de la Hipocicloide:
2 2 2
3 3 3
x y a 
y se representa paramétricamente como:
3
3
cos
:
x a t
f
y asen t
 


Determinar primera y segunda derivadas cuando
2 2
a
x y  .
)i A través de la forma implícita
)ii Con la forma paramétrica

41

42
DERIVABILIDAD Y CONTINUIDAD. DERIVADAS LATERALES
   ' '
0 0
lim y lim
x x
y y
f x f x
x x  
   
 
 
 
Teorema.      ' '
0 0 0'f x f x f x  
Relación entre la continuidad y la derivabilidad
Se estudia la continuidad y la derivabilidad de ambas en
0x  :
x
cosy x
2

 2
1y 
y x
x
2
y x
y x
2 2

43
Teorema. Si la función  y f x es derivable en 1x x ,
entonces también es continua para dicho valor de " "x .
Ejemplo. Estudiar la continuidad y la derivabilidad de la
función  
2
3
f x x en el punto donde 1 0x  .
Ejemplo. Estudiar la continuidad y la derivabilidad de la
siguiente función:
 
2
2 2 0
1 cos 0
2 2
7
7
x si x
f x x si x
x
si x





    

   
 
  


44

45
APLICACIONES GEOMÉTRICAS DE LA DERIVADA
La derivada como la pendiente de la recta tangente
Ejemplo. Obtener los ángulos que forman con el eje " "x las
tangentes a la curva  
2 2
4 4 ; 0x y y    , en los puntos:
     ) 2,0 ; ) 3, 3 ; ) 4,2i ii iii
Explicar los resultados mediante la gráfica de la curva.
Ejemplo. Calcular la pendiente de la tangente a la curva de
ecuación:
2
4y x 
en el punto  1, 3P  , así como el ángulo que forma dicha
tangente con el eje de las abscisas. Hacer una gráfica del
problema planteado.

46
Ejemplo. Determinar qué ángulo forma la curva 2
y x con la
recta 1x  al cortarse con ella. Hacer un trazo del problema
planteado.
Ejemplo. Determinar los puntos en los que las tangentes a la
curva de ecuación
5 4 3
23 11
3
5 2 3
x x x
y x    son paralelas al
eje " "x . Hacer un trazo aproximado de la gráfica de la curva,
considerando los puntos obtenidos.

47
Ejemplo. Determinar los puntos de la curva de ecuación
5
1 2
y
x


donde la tangente es paralela a la recta de
ecuación 2 5 5 0x y   . Hacer un trazo aproximado del
problema planteado con los resultados obtenidos.
Ejemplo. Obtener el punto de la curva 2 3
2y x donde su
tangente es perpendicular a la recta 4 3 2 0x y   .

48
Ecuaciones de la recta tangente y de la recta normal a una
curva en un punto dado
    1 1
1
; ' ;T N T N
T
y y m m x x m f x m
m
     
Ejemplo. Determinar las ecuaciones de las rectas tangente y
normal a la curva de ecuación 2
4 5y x x   en el punto
 3,2P . Hacer un trazo aproximado de la gráfica.
Ejemplo. Determinar las ecuaciones de las rectas tangente y
normal a la curva de ecuación 21
4
2
y x   en el punto
1
3,
2
P
 
 
 
. Representar gráficamente el problema planteado.

49
Ángulo de intersección entre dos curvas
   
   
2 0 1 02 1
2 1 2 0 1 0
' '
tan o bien tan
1 1 ' '
f x f xm m
ang ang
m m f x f x
 

 
 
Ejemplo. Determinar el ángulo que forman al cortarse las
curvas siguientes y graficar.
2
2 2
3
2
x
y y x y  
y

1C
2
 0 0,P x y
1
2C
1T
2T
x

50
Ejemplo. Demostrar que la elipse
2 2
2 6x y  y la parábola
2
4y x se cortan en un ángulo recto, es decir, que son curvas
ortogonales. Graficar aproximadamente.

51
APLICACIONES FÍSICAS DE LA DERIVADA
Razones de variación de variables relacionadas
  0media
; ; ; limmedia
t
s s s ds
s f t v v v v
t t t dt 
  
     
  
2
20media
; limmedia
t
v v dv d s
a a a a
t t dt dt 
 
     
 
Cinemática y Cálculo
Movimiento vertical. Caída libre
Cinemática:
0
0; 0f f
f
v v v
a v y a g g v gt
t t

      
2
0
0
2 2
; 0
2 2 2
f f
f f
f
v v tss sv
tt
v v v gt
v v v v gt s
   

       

Cálculo
2
;
2
gt ds
s v v v gt
dt
    
2
2
dv d s
a a a g
dt dt
    
Ejemplo. Se deja caer un objeto y cuando han transcurrido 3
segundos, se requiere conocer su velocidad. Determinarla:
)i A partir de la derivada del espacio recorrido.
)ii Por medio de la fórmula cinemática correspondiente.

52
Ejemplo. Un cierto tipo de aeronaves tienen como
especificaciones para el aterrizaje, entre otras, las siguientes:
una aceleración de frenado de 2
14,500
km
h
y sus distancias de
pista están dadas por la expresión: 2
250 7250s t t  donde
" "t es el tiempo en el que recorre la distancia de pista " "s .
)i Si aterriza con una velocidad de 250
km
h
, determinar su
velocidad a los 20 s de haber tocado tierra.
)ii Calcular la distancia total que recorre hasta detenerse y
el tiempo que tarda, suponiendo que desde que aterriza
frena hasta pararse totalmente.

53
Existen múltiples conceptos físicos en los que encuentran
aplicación las derivadas.
velocidad angular
d
dt


Se puede definir a la potencia mecánica instantánea como:
dT
P
dt

El gasto hidráulico, en un instante, se puede expresar como:
dV
Q
dt

Por otro lado, se puede tratar, para una determinada
resistencia eléctrica, a la intensidad de la corriente como la
derivada del voltaje con respecto a la le resistencia, esto es:
dV
I
dR

Existen problemas donde las variables experimentan razones
de variación con respecto al tiempo y para resolverlos juega
un papel de gran importancia la derivada.
Ejemplo. Una escalera indeformable, de 5.0 m de longitud, se
encuentra apoyada en un piso horizontal y reclinada en una
pared vertical. Si una persona jala la parte inferior de la
escalera, alejándola de la pared, a una velocidad de 1.5
m
s
,
¿con qué velocidad se deslizará hacia abajo la parte
superior en el instante en que está a 4 m del piso?

54
Ejemplo. Un globo esférico está perdiendo aire a una rapidez
de
3
100
dm
s
. ¿Con qué rapidez está disminuyendo su radio en
el instante en que mide 1m?
Ejemplo. Un vehículo se mueve en una carretera horizontal
recta. En un cierto punto de esta vía, sobre ella hay una torre
de 40 m en cuya punta se encuentra un observador. Si el
vehículo se mueve de manera que su velocidad angular con
respecto al observador es constante e igual a 0.10
rad
s
,
determinar la velocidad lineal del vehículo en las posiciones
correspondientes a 0 0
0 30y .

55
Ejemplo. La lámpara de un poste en la calle se localiza a una
altura de 3 m y una persona cuya estatura es de 1.70m se
aleja del poste con una velocidad de 2
m
s
. ¿Con qué
velocidad se alarga la sombra y cuánto mide ésta cuando la
persona se encuentra a 3 m de la base del poste?
Ejemplo. Una biela es un mecanismo elemental que
convierte un movimiento circular en rectilíneo y viceversa. La
biela de la figura se puede interpretar de cualquiera de las
dos maneras siguientes:
1. El eje de un motor se encuentra en " "O y hace girar el
brazo pequeño de la biela; ésta a su vez consigue que el
pistón " "P se mueva rectilínea y alternadamente hacia arriba
x
y
O
900 RPM 
B
A
10 cm
50 cm
P

56
y hacia abajo. (Este pistón puede ser el de una bomba
reciprocante, por ejemplo).
2. El pistón es el de un cilindro de motor de explosión interna
(como el de los automóviles) que, al deslizarse de arriba
abajo, hace girar el brazo menor de la biela y éste a su vez,
al eje de una rueda en " "O .
Para este problema se aceptará la interpretación  A . Si el
motor gira con una velocidad angular de 900 RPM y las
dimensiones son las de la figura, calcular la velocidad del
pistón cuando el punto " "B se encuentra sobre el eje de las
abscisas.
Ejemplo. Una rueda de la fortuna con un radio de 10 m da
una vuelta cada 3 min. Si el centro de la rueda está a 12 m
del piso, determinar la rapidez con que asciende un pasajero
cuando se encuentra a 18 m del piso.

57
Ejemplo. A un tanque cónico circular recto de radio 5R m y
altura 15H m , le entra un volumen de agua a razón de
3
1.5
min
m
. Determinar la rapidez de variación de la altura " "h
del agua cuando ésta se encuentra a 5 m del vértice.

58
Ejemplo. Un avión pasa sobre una ciudad " "A a las 12: 00 h,
a una velocidad constante de 1000
km
h
en dirección Este.
Media hora más tarde, a la misma altura y en dirección Sur,
otro avión sobrevuela la misma ciudad a una velocidad
constante de 1100
km
h
. ¿Con qué velocidad se separarán las
dos aeronaves a las 14: 00 h?
Ejemplo. Se tiene una pileta de 4.0 m de largo, cuya sección
transversal es un trapecio con altura de 60 cm y bases mayor
y menor de 1.2 40m y cm. Está siendo llenada con agua a
una velocidad de 90 litros por minuto. ¿A qué velocidad sube
el nivel del agua en el instante en que está a 25 cm del
fondo?

59
Ejemplo. Un faro fue construido en una pequeña isla situada
a 3 km de la costa, la cual, frente al faro es recta. El haz
luminoso del faro gira a una velocidad constante de 0.16
grados por minuto. Calcular la velocidad con la que se
desplaza la luz a lo largo de la costa, en un punto localizado
a 2.5 km del punto de la costa más próximo al faro.

60
LA DIFERENCIAL Y ALGUNAS APLICACIONES
Función diferenciable
Sea  y f x una función derivable en un cierto valor " "x para
el cual se cumple que  ' 0f x  . Luego, por la definición de
derivada, se tiene:
 
     0
lim ' ' ; 0 0
x
f x
f x f x f x x x x
x
 
 

          

Diferencial:    'dy df x f x x  
Ejemplo. Investigar si las siguientes funciones son
diferenciables, decir para qué valores de " "x y obtener sus
diferenciales:
   2 2
) 2 5 6 ; ) 1i f x x x ii f x x     
Diferencial de la función identidad
 
 
 
' ; 1
' 1
y f x x
dy f x x dy x dy xdy
f x
dx
 
        
 
Como y x dy dx   ; entonces dx x 

61
Diferencial:  '
dy
dy dx f x dx
dx
 
Ejemplo. Obtener la diferencial de las siguientes funciones:
 3 2 3
) 2 3 7 ; ) tan 1i y x x x ii f x x     
) seciii y ang x

62
Interpretación geométrica de la diferencial
 'm y f x x   
La derivada como cociente de diferenciales
   ' '
dy
dy f x dx f x
dx
  
Permanencia de la forma de la diferencial para una función
de función
 
 
  ;
y f u dy dy du dy du
y f g x dy dx
dx du dx du dxu g x
   
      
  
Diferenciales sucesivas
     2 2 3 3
' ; '' ; '''dy f x dx d y f x dx d y f x dx  
   
   
...
n n n
d y f x dx
Ejemplo. Calcular las diferenciales de primero y segundo
orden para la función:
  3 2
2 cosf x x x 
x
y
f
m y
y
x
y
x
y y 
x x 
B
CA
recta
tangente

63
ERRORES, VALORES APROXIMADOS Y APLICACIONES DE LA
DIFERENCIAL
 
 
'
' 100 100
100
A
A
R
A
R
R
y dy x
yy f x x x
dy f x x P
y
dy dy
P
y y


 






     

 
      
 
       

   

Ejemplo. Dada la función   5f x x  , determinar el
incremento y y la diferencial dy para 23x  y 3x  .
Calcular también los errores absoluto y relativo, así como el
porcentaje del error al utilizar a la diferencial en lugar del
valor exacto del incremento de la función.

64
Ejemplo. Por medio de diferenciales, obtener un valor
aproximado de 27 .
Ejemplo. Por medio de diferenciales obtener el valor
aproximado de tan44º.
Ejemplo. A una cúpula semiesférica con radio exterior de
5 m, se le aplica un impermeabilizante especial que tiene un
espesor de 1cm. ¿Cuánto se gasta de manera aproximada
(mediante diferenciales) en impermeabilizante si el litro
cuesta $100.00? Calcular también la cantidad exacta que se
invierte, así como el porcentaje de error que se comete al
utilizar la diferencial en lugar del valor exacto.

65
Ejemplo. Las fórmulas para el área y el volumen de una
esfera son, respectivamente:
2 34
4 y
3
A r V r  
Al medir el radio se obtiene que: 3r m :
)i ¿Cuáles son los errores máximos aproximados de
A y V si al medir el radio su medida puede variar 1cm?
)ii ¿Cuál es en cada caso el porcentaje de error?

66
Ejemplo. En un laboratorio de materiales se trabaja con
sólidos metálicos en forma de cubos. Si uno de éstos, que
tiene 10 cm de arista, se somete a una determinada
temperatura, se dilata aumentando su arista 2 mm, ¿cuáles
serán los incrementos exacto y aproximado en su volumen y
qué porcentaje de error se comete al utilizar la diferencial en
lugar del incremento exacto?
Ejemplo. Unos cilindros circulares rectos, utilizados en un
laboratorio, tienen 20 cm de longitud, un diámetro interior de
10 cm y un diámetro exterior de 10.4 cm. Por medio de la
diferencial, calcular el costo de cada cilindro, si el material
del cual están hechos cuesta 3
$ 5.00/cm .

67
Ejemplo. En la orilla de la parte superior de un edificio hay
una lámpara que proyecta la sombra de un poste de 3.2 m
que se encuentra a 11.75 m de la base del edificio. Si la
sombra del poste es de 90 cm con un posible error de 1cm
en su medición, ¿cuál es la altura aproximada del edificio y
cuál el porcentaje de error en su cálculo?

Capítulo 4. Derivada y aplicaciones

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Destacado

Destacado (8)

Similar a Capítulo 4. Derivada y aplicaciones

Similar a Capítulo 4. Derivada y aplicaciones (20)

Más de Pablo García y Colomé

Más de Pablo García y Colomé (12)

Último

Último (20)

Capítulo 4. Derivada y aplicaciones