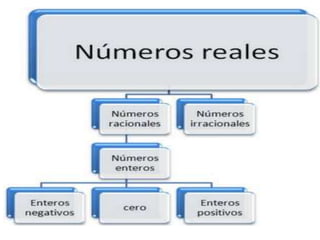
Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros y pueden describirse como aquellos cuya representación decimal es eventualmente periódica. Los números reales incluyen tanto a los números racionales como a los números irracionales, que no pueden expresarse como fracciones de números enteros. El conjunto de números reales es denso, ordenado y completo.