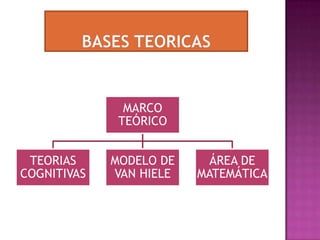
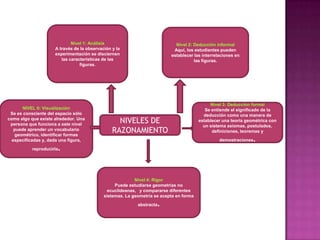
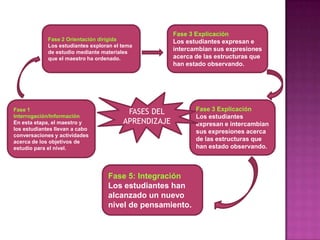
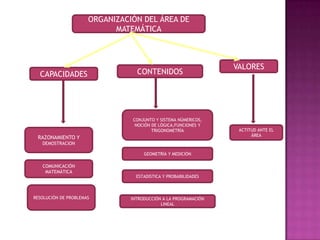
1. El documento presenta un proyecto de investigación que busca mejorar el aprendizaje de la semejanza de triángulos en estudiantes de cuarto grado mediante la aplicación del modelo de van Hiele. 2. El problema general es determinar si la aplicación del modelo de van Hiele mejorará significativamente el aprendizaje de semejanza de triángulos y el objetivo general es mejorar dicho aprendizaje mediante dicho modelo. 3. Se revisan los antecedentes de investigaciones previas relacionadas al tema.

1. PROYECTO DE
INVESTIGACION
INTEGRANTE:
PRESENTACIÓN
OSCANOA, ELVA
ROSE

2.  TITULO: El modelo de van hiele en la
enseñanza de semejanza de triángulos en
alumnos de 4to grado de educación secundaria.
 PROBLEMA GENERAL: ¿La
aplicación del
modelo de van hiele mejorará
significativamente el aprendizaje de
semejanza de triángulos en alumnos
de 4to grado de educación
secundaria?
 OBJETIVO GENERAL: Mejorar
significativamente
el aprendizaje de semejanza de triángulos
en alumnos de 4to grado mediante la
aplicación del modelo de van hiele.

3. ANTECEDENTES

4.  AUTOR:FLORES NÚÑEZ, Enrique Moisés
 AÑO DE PUBLICACION:2
 OBGETIVOS:
 Identificar el nivel de razonamiento analítico que
presentan los alumnos del 4to grado del C.E.
“Jorge Basadre”.
 Establecer el nivel de contribución del uso del
Integrador Geométrico en el aprendizaje en los
alumnos del cuarto grado del C.E. “Jorge Basadre”
para desarrollar su capacidad de razonamiento
analítico.
 Evaluar la eficacia del Integrador Geométrico en el
desarrollo de la capacidad de razonamiento
analítico de los estudiantes del 4to grado del C.E.
“Jorge Basadre”.

5.  METODOLOGIA:
 LA METODOLOGÍA USADA EN LA INVESTIGACIÓN FUE
DE TIPO APLICADA, EL NIVEL EXPERIMENTAL Y EL
DISEÑO CUASI – EXPERIMENTAL.
 CONCLUSIONES:
 EL USO DEL INTEGRADOR GEOMÉTRICO EN
ACTIVIDADES DE APRENDIZAJE DE LA GEOMETRÍA
DESARROLLÓ LA CAPACIDAD DE RAZONAMIENTO
ANALÍTICO EN LOS ESTUDIANTES DEL 4º DEL C.E.
“JORGE BASADRE”.
 EL USO DEL INTEGRADOR GEOMÉTRICO INCREMENTÓ
SIGNIFICATIVAMENTE EL DESARROLLO DE DESTREZAS,
HABILIDADES Y LA CAPACIDAD DE RAZONAMIENTO
ANALÍTICO DE LOS ESTUDIANTES DEL 4º DEL C.E.
“JORGE BASADRE”.
 EL USO DEL INTEGRADOR GEOMÉTRICO CONTRIBUYE
EN LA FORMACIÓN DE LA CAPACIDAD DE
RAZONAMIENTO EN EL NIVEL DE ANÁLISIS DE LOS
ESTUDIANTES DEL C.E. “JORGE BASADRE”.

6.  AUTOR:ARCHI GARCIA, Vetty Maribel y
PAUCAR SOCUALAYA, Mérida Maria,
 AÑO DE PUBLICACION: 2011
 METODOLOGIA:
En el trabajo de investigación mencionado se
utilizó el método experimental. El diseño de
investigación utilizado fue el Cuasi –
Experimental, con dos grupos: grupo control
y grupo experimental.

7.  LA UTILIZACIÓN DEL TANGRAM PERMITE EN EL
GRUPO EXPERIMENTAL INCREMENTAR DE 10 A 12
ALUMNOS, DENTRO DEL NIVEL DE
COMPRENSIÓN.
 LA EXPERIMENTACIÓN DEL TANGRAM PERMITE
INCREMENTAR EL NIVEL DE APLICACIÓN DE 6 A
24 ALUMNOS, RESPECTO AL TEMA DE ÁREAS DE
REGIONES POLIGONALES, EN ALUMNOS DEL
CUARTO GRADO DE EDUCACIÓN SECUNDARIA.
 EL USO DEL TANGRAM PERMITE INCREMENTAR,
EN LOS ALUMNOS, EL NIVEL DE APLICACIÓN EN
LA SOLUCIÓN DE PROBLEMAS.

8.  AUTOR:BARRETO ASTO, Edgar y VILLANUEVA
RAVILLA, Carlos David
 AÑO DE PUBLICACION: 2010
 METODOLOGIA:
 EL MENCIONADO TRABAJO SE REALIZÓ
UTILIZANDO LA SIGUIENTE METODOLOGÍA: EL
NIVEL DE INVESTIGACIÓN: FUE
EXPERIMENTAL, EL TIPO DE INVESTIGACIÓN
FUE APLICADA Y EL DISEÑO UTILIZADO FUE EL
CUASI – EXPERIMENTAL. TRABAJARON CON
DOS GRUPOS

9. 1. LA UTILIZACIÓN DE LAS HOJAS DE LAS PLANTAS
CONTRIBUYÓ FAVORABLEMENTE EN EL
DESARROLLO DE LAS CAPACIDADES DE
COMPRENSIÓN Y APLICACIÓN DE PERÍMETROS Y
ÁREAS DE FIGURAS GEOMÉTRICAS EN LOS
ALUMNOS DE LA I.E. “JOSÉ CARLOS
MARIÁTEGUI” – HUANCAYO.
2. . LAS UNIDADES DIDÁCTICAS DE NUESTRA
PROPUESTA, MEDIANTE EL USO DE LAS HOJAS DE
LAS PLANTAS FUERON OPERATIVAS DEBIDO A SU
FUNCIONALIDAD EN EL PROCESO DEL
APRENDIZAJE DE PERÍMETROS Y ÁREAS DE
FIGURAS GEOMÉTRICAS, EN ALUMNOS DEL 3º
GRADO DE EDUCACIÓN SECUNDARIA DE LA I.E.
“JOSÉ CARLOS MARIÁTEGUI “ – HUANCAYO.
3. LAS HOJAS DE PLANTAS SON RECURSOS
DIDÁCTICOS ADECUADOS PARA EL ÁREA DE
MATEMÁTICA, COMPONENTE GEOMETRÍA

10.  AUTOR: CARLOS RUDAS, Miriam Geovanna y HUAMANI
FERNANDEZ.
 AÑO DE PUBLICACION:2009
 OBJETIVO:
 ESTABLECES FORMAS Y MANERAS DE ELEVAR EL NIVEL DE
LOGRO DEL APRENDIZAJE DE SÓLIDOS GEOMÉTRICOS, EN
ALUMNOS DEL CUARTO GRADO DE EDUCACIÓN
SECUNDARÍA DE LA I.E “JOSÉ CARLOS MARIÁTEGUI”
HUANCAYO
 DISEÑAR LA FORMA O MANERA DE ELEVAR EL LOGRO DE
APRENDIZAJE DE SÓLIDOS GEOMÉTRICOS.
 EXPERIMENTAR DEL DISEÑO DE LA FORMA QUE PERMITA
ELEVAR EL NIVEL DE LOGRO DEL APRENDIZAJE DE
SÓLIDOS GEOMÉTRICOS.
 DETERMINAR EL NIVEL DE LOGRO DEL APRENDIZAJE DE
SÓLIDOS GEOMÉTRICOS EN LOS ALUMNOS AL INICIO Y
DURANTE EL EXPERIMENTO.

11.  lametodología utilizada en el
trabajo de investigación fue: el tipo
de investigación fue aplicado, el nivel
de investigación fue experimental con
diseño pre-experimental, de un solo
grupo, con pre-test y pos test.

12.  La utilización de material didáctico
(elaborado con objeto recuperable)
eleva el nivel de logro de aprendizaje de
sólidos geométricos, en alumnos de
cuarto grado de Educación Secundaria.
 El material didáctico (elaborado con
objeto recuperable) favorece el
trabajo socializado en los alumnos del
cuarto grado de educación Secundaria.
 La utilización sistemática de material
elaborado con objeto recuperable)
favorece el mejoramiento del
aprendizaje de sólidos geométricos.
 El material didáctico (elaboración con
objetos recuperables) es de bajo costo y
ofrece una gran diversidad de
explicaciones para favorecer el

13.  AUTOR:por la Mg. Cecilia Procopio Martínez
 OBJETIVO: El objetivo de la investigación es
la realización de un estudio exploratorio
sobre la manipulación concreta del doblado
de papel y su relación con el establecimiento
de conexiones entre la geometría y el
álgebra que efectúan los alumnos de segundo
grado de secundaria durante la resolución de
problemas sobre los contenidos de polígonos
y variables algebraicas.

14.  Lainvestigadora considera en su marco
teórico el Modelo de Van Hiele. La
metodología de investigación utilizada
consiste en lo siguiente: el estudio
exploratorio se realizará a un grupo de
alumnos de segundo grado de secundaria. La
indagación de evidencias de las conexiones
involucradas en la actividad concreta será a
través de la observación de:

15.  Las secuencias didácticas para la enseñanza de
las construcciones de polígonos con doblado de
papel.
 La resolución de problemas geométricos y
algebraicos específicos.
 Las sesiones se grabarán, anotándose en un
registro en donde se describirá o relatará en
forma exacta y concreta, lo que el alumno dijo
o hizo espontáneamente en una situación
específica. Agregando posteriormente su
interpretación.

16. Lo coincidente del trabajo
descrito con el mío que ambos
se basan en el Modelo de Van
Hiele. La Diferencia es que la
variable independiente es el uso
de la estrategia doblado de
papel, mientras que en el
nuestro es el modelo en si, por
los considerandos anteriormente
mencionados.

17. MARCO
TEÓRICO
TEORIAS MODELO DE ÁREA DE
COGNITIVAS VAN HIELE MATEMÁTICA

18. AUSUBEL
 APRENDIZAJE SIGNIFICATIVO
RELACIONAR LA INFORMACION
NUEVA CON LO QUE EL
ALUMNO YA SABE
(CONOCIMIENTOS PREVIOS)

19.  Ausubel sustenta que tanto el
aprendizaje por recepción o por
descubrimiento, pueden ser o
repetitivos o significativos, según como
ocurran las condiciones del
aprendizaje. Y es que en su propuesta,
por un lado aprendizaje por recepción
y aprendizaje por descubrimiento
constituyen una dimensión mientras
que otra dimensión distinta lo
constituyen el aprendizaje repetitivo o
memorístico y el aprendizaje
significativo.

20. Para que un aprendizaje sea
potencialmente significativo
es que la nueva informacion
interactue con la estructura
cognitiva previa y que exista
una disposicion para ello del
que aprenda.

21. APRENDIZAJE POR DESCUBRIMIENTO
APRENDIZAJE GUIADO
MODO DE APRENDIZAJE
 ENACTIVO
 ICONO
 SIMBOLICO

22. Bruner destaca por sus aportes teóricos acerca
del aprendizaje de la matemática y el desarrollo
de las capacidades que permitieran un manejo
abstracto de los conceptos y propiedades
matemáticas. Sin embargo los aportes de Bruner
que fueron ampliamente difundidos son los
referidos al “Aprendizaje por Descubrimiento”,
“Modos de Representación del Conocimiento” y
su “Secuencia Instrucciones.
 La teoría de Bruner incidió sobre la importancia
que tiene para el aprendizaje el descubrir el
conocimiento, para que éste resulte real y útil.
Plantea que los maestros deben planificar
situaciones problemas que estimulen a los
estudiantes a descubrir por si mismos, la
estructura del material de la asignatura, las
ideas fundamentales. Los hechos específicos y
los detalles para Bruner no forman parte de la
estructura”.

23.  Z.D.P.
 INTERACCION
 MEDIACION
 POTENCIAR

24.  La zona de Desarrollo Próximo de Vygotski
 Del trabajo de Vygotski el concepto de
“Zona de Desarrollo Próximo” (ZDP) es la
parte más conocida y a la que con más
frecuencia se recurre para repensar diversos
aspectos del desarrollo humano, sobre todo
en escenarios educativos. Vygotski definió la
Zona (ZDP) como:
 “ … la distancia entre el nivel de desarrollo real del niño tal y
como puede ser determinado a partir de la resolución
independiente de problemas” y el nivel más elevado de
“desarrollo potencial y tal como es determinado por la
resolución de problemas bajo la guía del adulto o en
colaboración con iguales más capaces”. (VYGOTSKI) en (VALLEJO;
1999 en http://www.jalisco.gob.mx/srias/educacion)

25. NIVELES DE RAZONAMIENTO FASES DE APRENDIZAJE
Es la descripción de El avance atreves de
los distintos niveles los niveles depende mas
del razonamiento de la instrucción que se
geométrico que los reciba que de la edad o
madurez. Van Hiele
estudiantes transitan
propuso cinco fases
a lo largo de su
secuenciales de
formación aprendiza
matemática

26. Nivel 1: Análisis Nivel 2: Deducción informal
A través de la observación y la Aquí, los estudiantes pueden
experimentación se disciernen establecer las interrelaciones en
las características de las las figuras.
figuras.
Nivel 3: Deducción formal
NIVEL 0: Visualización Se entiende el significado de la
Se es consciente del espacio sólo deducción como una manera de
como algo que existe alrededor. Una
persona que funciona a este nivel
NIVELES DE establecer una teoría geométrica con
un sistema axiomas, postulados,
puede aprender un vocabulario
geométrico, identificar formas
RAZONAMIENTO definiciones, teoremas y
especificadas y, dada una figura, demostraciones .
.
reproducirla
Nivel 4: Rigor
Puede estudiarse geometrías no
ecuclideanas, y compararse diferentes
sistemas. La geometría se acepta en forma
abstracta .

27. Fase 3 Explicación
Fase 2 Orientación dirigida Los estudiantes expresan e
Los estudiantes exploran el tema
de estudio mediante materiales
intercambian sus expresiones
que el maestro ha ordenado. acerca de las estructuras que
han estado observando.
Fase 1
Interrogación/Información
FASES DEL Fase 3 Explicación
Los estudiantes
En esta etapa, el maestro y APRENDIZAJE expresan e intercambian
los estudiantes llevan a cabo
sus expresiones acerca
conversaciones y actividades
acerca de los objetivos de de las estructuras que
estudio para el nivel. han estado observando.
Fase 5: Integración
Los estudiantes han
alcanzado un nuevo
nivel de pensamiento.

28. ORGANIZACIÓN DEL ÁREA DE
MATEMÁTICA
VALORES
CAPACIDADES CONTENIDOS
CONJUNTO Y SISTEMA NÚMERICOS,
NOCIÓN DE LÓGICA,FUNCIONES Y
TRIGONOMETRÍA ACTITUD ANTE EL
ÁREA
RAZONAMIENTO Y
DEMOSTRACION
GEOMETRÍA Y MEDICIÓN
COMUNICACIÓN
MATEMÁTICA
ESTADISTICA Y PROBABILIDADES
RESOLUCIÓN DE PROBLEMAS INTRODUCCIÓN A LA PROGRAMACIÓN
LINEAL

29. Las técnicas e instrumentos que utilizare en el
trabajo de investigación se muestra en el
cuadro
TÉCNICAS INSTRUMENTOS
PRUEBA PRE – TEST
PRUEBAS ESCRITAS
PRUEBA POST – TEST

31.  GRAC