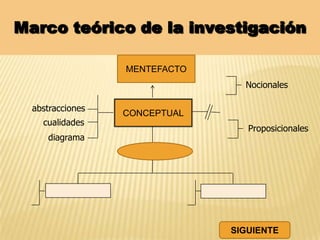
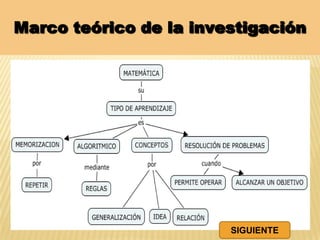
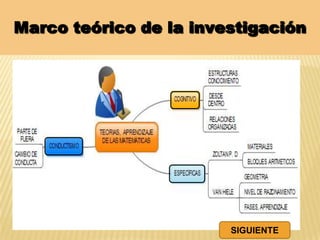
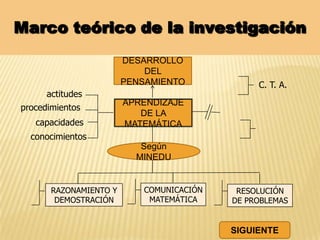
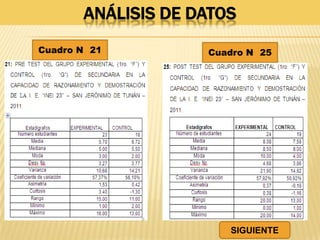
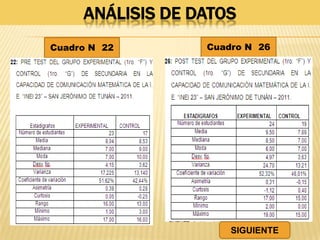
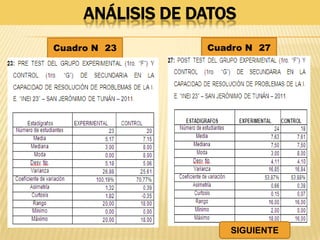
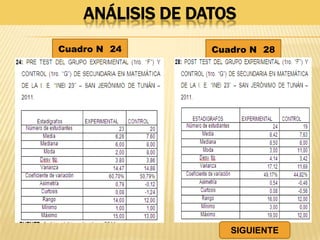
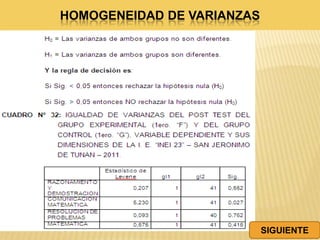
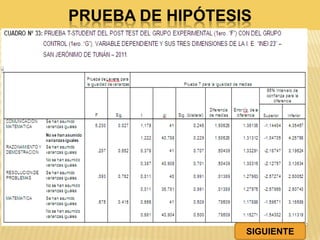
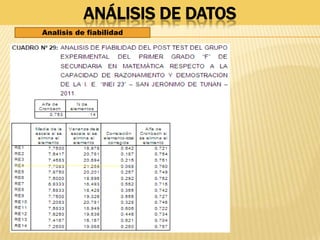
Este documento resume una tesis de maestría que investiga la influencia del "mentefacto conceptual" en el aprendizaje de las matemáticas en estudiantes de primer grado de secundaria en Perú. El estudio busca determinar cómo el mentefacto conceptual afecta el desarrollo de la capacidad de razonamiento, comunicación matemática y resolución de problemas. El documento presenta el marco teórico, metodología y resultados de pruebas aplicadas a 53 estudiantes para medir el impacto del mentefacto conceptual en sus habilidades