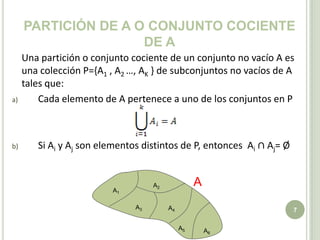
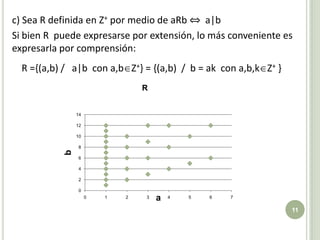
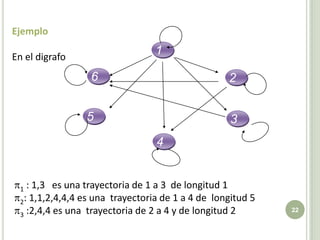
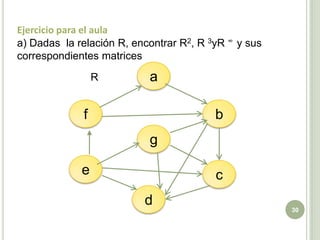
El documento aborda la teoría de relaciones binarias en matemáticas discretas, destacando su importancia en computación. Se define el concepto de par ordenado y producto cartesiano, junto con ejercicios prácticos para entender su aplicación. Además, se exploran temas como particiones, representación matricial y digrafos, ilustrados con ejemplos y ejercicios para facilitar la comprensión.

1. MATEMATICA DISCRETAUNIDAD Nº 31º parteRelaciones yDigrafosTEORIABibliografía: Estructuras de Matemáticas Discretas para Computación.Kolman y Busby. Cap IV y VII1

2. relaciones binariasUna estructura de datos, tal como un arreglo, lista o árbol es generalmente usada para representar simultáneamente a un conjunto de datos y a una relación que se cumple entre los miembros del conjunto. El caso particular de relaciones binarias merece ser tratado aparte, por la riqueza de conceptos y resultados a que da lugar y el tipo de técnicas que pueden utilizarse. Es por ello que en esta unidad estudiaremos formalmente a las relaciones binarias, conjunto de parejas de objetos que comparten algunas características o propiedades en común. Las mismas son de fundamental importancia en computación.Para poder introducir el concepto de relación binaria necesitamos precisar lo que significa una pareja ordenada de objetos y definir el producto cartesiano de dos conjuntos.2

3. par ordenado Un par ordenado (a, b) es una lista de dos objetos a y b en un orden preestablecido, donde a se dice primera componente y b segunda componente. Un par ordenado es una secuencia de longitud 2. Se denota entre paréntesis y separadas las componentes por una coma: (a,b) Por definición, (a,b)  (b,a)Igualdad entre pares ordenados Definición: (a1, b1) = (a2, b2) si y solo si a1 = a2 y b1= b2 Conjunto producto CARTESIANO Definición: Si A y B son conjuntos no vacíos, se define el conjunto producto cartesiano A x B del siguiente modoA x B = { (a, b) / aA y bB }3

4. Ejercicio para el aula: Sean A = {1, 2} y B = {a, b, c} Calcule A x B y B x A . ¿Es conmutativo el producto cartesiano? Observe que los elementos de AxB y BxA pueden ser dispuestos en forma tabular del siguiente modoteoremaPara dos conjuntos finitos no vacíos A y B se cumple que |A x B|= |A|. |B|El cardinal del producto es igual al producto de los cardinales4

5. Ejercicio para el aulaUna compañía de investigación de mercados clasifica a una persona de acuerdo con los siguientes criterios:Género: masculino (m); femenino (f)Máximo nivel de educación terminado: escuela primaria (p); secundaria (s); universidad (u); posgrado (g).Sean S ={m,f} y L={p,s,u,g} Forme SxL y diga que representa5

6. Generalización: producto cartesiano de n conjuntos Sean A1 , A2 , ….. , An conjuntos , se define A1xA2x…xAn={ (a1, a2, … ,an) / ai Ai , i = 1, 2,… , n} Si cadaconjunto Aiesfinito se tieneque |A1xA2x…xAn| = | A1 | . |A2| . ….|An|6

7. partición de A o Conjunto cociente de A Una partición o conjunto cociente de un conjunto no vacío A es una colección P={A1 , A2 …, AK } de subconjuntos no vacíos de A tales que:Cada elemento de A pertenece a uno de los conjuntos en PSi Ai y Aj son elementos distintos de P, entonces Ai∩ Aj= ØAA2A1A3A4A5A67

8. Ejercicio para el aula:a) Sea A = {a, b, c, d, e, f, g, h}. ¿Cuáles de los siguientes subconjuntos forman una partición de A?A1 = {a, b, c, d} A2 = {a, c, f, g, h} A3= {a, c, e, g} A4 = {b, d} A5 = {f, h}b) Dados los siguientes conjuntos, encuentre por lo menos una partición para cada uno: i) ii) A={xN / x es múltiplo de 3}iii) A={ x / x es una letra de la palabra paralelepípedo}iv) A={ (a,b) / a, b {1,2,3} } v) A={ (a,b) / a,b N}8

9. RelaciónDefinición: Sean A y B conjuntos no vacios. Una relación R de A en B es cualquier subconjunto del producto cartesiano AxB. Simbólicamente : Cualquier conjunto R tal que R ⊆AxB se dice Relación de A en BCaso particular:Si A = B se dice que R está definida en A y se expresa R ⊆ A x A Notación : Cuando a está relacionada con b por medio de R escribiremos (a,b)R oaRb9

10. ejemplosa) Sean A={Pablo,Juan,Carlos} y B={Fiat,Peugeot,Chevrolet,Renault} y sea R definida del siguiente modoaRb⇔ “a prefiere la marca b” Entonces la enumeración de los elementos de R podría ser:R={(Pablo,Chevrolet),(Juan,Fiat),(Juan,Renault),(Carlos,Peugeot)}b) Sea R definida en N por medio de la condición a Rb ⇔ a = b2 Entonces R = { (1,1),(4,2),(9,3),(16,4),…} es un conjunto infinito, por lo tanto conviene definirlo por comprensión o propiedad Se tendrá R = { (a,b) NxN /a = b2 }10

11. c) Sea R definida en Z+ por medio de aRb⇔a|bSi bien R puede expresarse por extensión, lo más conveniente es expresarla por comprensión: R ={(a,b)/ a|b con a,bZ+} = {(a,b) / b = ak con a,b,kZ+ }11

12. Conjuntos que surgen de las relaciones:Sea R de A en B, se definen: Dominio de R : Conjunto de elementos de A que están relacionados con algún elemento de B mediante la relación RRango de R: Conjunto de elementos de B que están relacionados con algún elemento de A por medio de R Si x  A , se define el Conjunto relativo en R de x como el conjunto de todos los elementos de B relacionados con x . Simbólicamente se expresa R(x)={y B / xRy}En el Ejemplo c)Dom R = Z+Rango R = Z+R(1) = { 1,2,3,4,5,…} = Z+ , R(2) = { 2,4,6,8,…} , R(3) = {3,6,9,12,15,…}etc12

13. MATRIZ DE UNA RELACIÓNSi A= {a1,a2,…,am} y B={b1,b2,…,bn} son conjuntos finitos que contienen m y n elementos, respectivamente, y si R es una relación de A en B, se representa R por la matriz MR definida como MR se dice matriz de R y es una matriz booleana de orden mxn. A menudo MR proporciona una manera fácil de verificar si tiene una propiedad dada.13

14. Ejercicio para el aulaSea A = { Ana , Carlos , Javier , Victor} y B = { M , F} y sea R la relación que vincula a cada persona con su sexo. EntoncesR= { (Ana,F),(Carlos,M),(Javier,M),(Victor,M)}La matriz que representa a R es Teorema: Toda relación definida en conjuntos finitos tiene representación matricial booleana y recíprocamente toda matriz booleana representa una relación.Ejercicio para el aulaDeducir la relación definida en A representada por la siguiente matriz booleana14

15. GRAFO DIRIGIDO O DIGRAFO DE R Si A es un conjunto finito y R una relación definida en A, se puede representar a R de modo gráfico siguiendo las instrucciones que se dan a continuación:Se representa con un círculo o simplemente con un punto a cada elemento de A.

16. Se dibuja una flecha del vértice aial vértice aj si y solo si (ai,aj)∈R Esta representación gráfica se llama Grafo Dirigido o Digrafo de R. Los círculos se dicen nodos o vértices y las flechas se dicen aristas o arcos del Digrafo Al conjunto de vértices o nodos se le representa con V y al conjunto de aristas con la letra E. Se denota digrafo G=(V,E)15

17. Ejercicio para el aulaSea A = { 1 ,2,3,4,5,6} y sea R en A definida por aRba|bConfeccionar el Digrafo y la matriz de R.Observe que: Debido a que cada número es divisor de si mismo , en el grafo cada elemento de A tendrá un lazo (flecha que sale de un vértice e ingresa al mismo) . Esta particularidad se verá reflejada en la diagonal de la matriz.

18. Como 1 es divisor de todos los números, del vértice etiquetado con 1 saldrán flechas hacia todos los elementos de A. Esto se observará en la 1º fila de la matriz

19. 4 , 5 y 6 sólo son divisores de si mismo por lo que de ellos saldrá una única arista, un lazo. Y en la matriz se observará en las filas correspondientes la presencia del único 1 que representa al lazo correspondiente16

20. El grafo y la matriz correspondientes son16253417

21. Ejercicio para el aula Para las siguientes relaciones confeccione el digrafo de R y encuentre su matrizA = { 1 ,2,3,4,5,6} y sea R en A definida por aRba+bes par A = { a,b,c,d} y R = {(a,a),(a,b),(b,c),(c,d),(b,b),(c,c),(d,d),(a,c),(a,b) ,(b,d)}18

22. 162534Respuesta de a) Observe que se han formado dos grupos de elementos, por un lado los numeros pares relacionados todos entre si y por otro lado los impares todos entre si. Ninguna arista va de un par a un impar ni a la inversa.Se ha producido una partición P del conjunto AP = { {1,3,5},{2,4,6}}19

23. Otros conceptos importantes: Si R es una relación en A y si a∈A entonces el grado interno de a es el número de nodos b∈A tal que (b,a)∈R Mientras que el grado externo de a es el número de nodos b∈A tal que (a,b)∈R Esto significa , en términos del digrafo de R, que el grado interno de un vértice es el número de arcos que terminan en el vértice y el grado externo es el número de arcos que salen del vértice.Ejercicio para el aula Sea A={a,b,c,d} y sea R la relación sobre A que tiene la matriz Construya el digrafo de R y haga una lista de los grados internos y externos de todos los vértices20

24. TRAYECTORIAS EN RELACIONES Y DIGRAFOS Sea R en A. Una trayectoria de longitud n de aab es una sucesión finita que comienza con a y termina en b tal queSi están involucrados n+1 elementos de A, no necesariamente distintos, se dice que es una trayectoria de longitud n. Una trayectoria se concibe visualmente con más facilidad con ayuda del digrafo de la relación. Aparece como una trayectoria geométrica o sucesión de arcos, y de hecho el nombre de trayectoria es debido a esta representación. En consecuencia, la longitud de una trayectoria es el número de arcos que hay en la misma, en donde los vértices no necesitan ser todos distintos 21

25. 162534Ejemplo En el digrafo 1 : 1,3 es una trayectoria de 1 a 3 de longitud 12: 1,1,2,4,4,4 es una trayectoria de 1 a 4 de longitud 5 3:2,4,4 es una trayectoria de 2 a 4 y de longitud 222

26. Las trayectorias pueden usarse para definir otras relaciones vinculadas a una R dada. Definición de RnSi n N , se define una relación Rn en A como sigue: a Rn b existe una trayectoria de longitud n de a a b en RCaso particulara R2 b  existe una trayectoria de longitud 2 de a a b en RDefinición de Ra R b  existe una trayectoria de cualquier longitud de a a b en RR se llama relación de conectividad23

27. Ejercicio para el aula Sea R la relación dada por el siguiente grafo 4fabdecEncuentre los digrafos de R2, R3 y R24

28. R2 es la relación tal que vincula a los elementos de A unidos por una trayectoria de longitud 2 en RSe observa que aR2c , aR2d, cR2d, fR2d, cR2c, etc Pero sin embargo aR2b , cR2e R3 es la relación tal que vincula a los elementos de A unidos por una trayectoria de longitud 3 en RSe observa que aR3c , aR3d, cR3d, bR3d, bR3c, etc Pero sin embargo aR3b , cR3e25

29. 4fabdec4fabdecLos grafos de R2y R3 son R2R326

30. TeoremaPara n N y R definida en A se tiene que ( n factores) Donde es el símbolo que representa al producto booleano de matrices 27

31. 284fabdecEn el ejemplo se tiene que para R y R2 sus respectivas matrices son 4fabdec