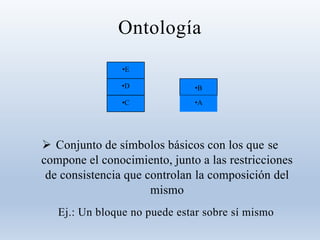
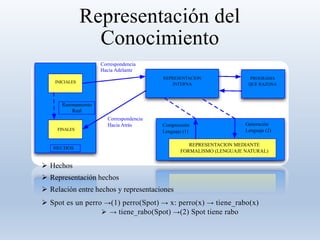
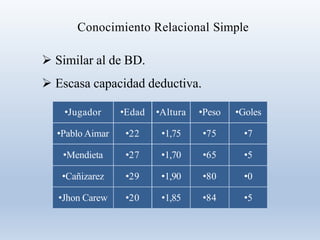
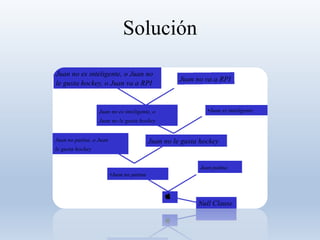
Este documento presenta información sobre la representación del conocimiento en inteligencia artificial. Brevemente describe algunas propiedades del conocimiento como que es voluminoso, difícil de caracterizar con precisión e incierto. Luego explica que una representación del conocimiento debe ser capaz de captar generalizaciones, ser comprensible y modificable, entre otras cosas. Finalmente, introduce conceptos como ontología, hechos, representación de hechos, lógica proposicional y métodos de representación basados en lógica.