Este documento describe los métodos para calcular las pérdidas de presión en tuberías debido a la fricción y accesorios. Explica las ecuaciones de Hagen-Poiseuille, Darcy-Weisbach y Colebrook para calcular la pérdida primaria en régimen laminar y turbulento. También presenta expresiones analíticas, coeficientes experimentales y la longitud equivalente para evaluar las pérdidas secundarias en codos, válvulas y otros accesorios. Por último, detalla el cálculo total de la pérdida

1. 1
RESUMEN
PÉRDIDA PRIMARIA
 El cálculo de la perdida de presión para régimen de flujo laminar, se
puede realizar con la ecuación de Hagen - Poiseuille, en la forma:
El volumen, en m 3
/ s; la pérdida de presión, en Pa; el diámetro interior
de la tubería, en m; la viscosidad absoluta, en Pa.s y la longitud, en m.
 El cálculo de la perdida por fricción, para régimen de flujo laminar y
régimen de flujo turbulento se realiza mediante la ecuación de Darcy –
Weisbach :
2
2
L V
hf f
D g

Para la determinación del factor de fricción f , se dispone de dos alternativas :
A. El uso del Diagrama de Moody, y el uso de
B. Ecuaciones semi-empíricas :
Régimen laminar:
Régimen turbulento:
El número de Reynolds:
En general, para tuberías de uso industrial:
Re < 2000 Régimen laminar
2000 < Re < 2300 Régimen crítico
2300 < Re < 4000 Régimen transición
4000 < Re Régimen Turbulento
4
128
p D
L



 
64
Re
f 
5 2,51
2 log [ ]
3,71Re
f
f

  


D
DVDV 

4
Re

2. 2
DIAGRAMA DE MOODY
Rugosidad promedio de tubos comerciales
Material nuevo e (mm)
Vidrio 0,0003
Tubería estirada 0,0015
Acero, hierro forjado 0,046
Hierro fundido asfaltado 0,12
Hierro galvanizado
0,15
Hierro fundido 0,26
Madera cepillada 0,18- 0,9
Concreto 0,3 – 3,0
Acero remachado 0,9 – 9,0

3. 3
8.2. Petróleo es bombeado a razón de 0,0283 m3/s; a través de una tubería de
15,24 cm de diámetro interior construida de acero (e = 0,046 mm), la longitud
de la tubería es de 310 m.
a. Si el petróleo es bombeado a 30°C, y la tubería está horizontal:
a.1. ¿Cuál es la pérdida de energía en metros del fluido?.
a.2 ¿Cuál será la presión indicada por el manómetro colocado
al final de la tubería, si al inicio de la tubería otro manómetro
indica 31,74 bar?.
a.3. ¿Cuál será la potencia requerida por la bomba, considerando
una eficiencia del 80 %?.
b. Idem que (a) pero la tubería es vertical y el flujo es ascendente.
c. Si el petróleo se bombea a 120°C, y la tubería está horizontal:
c1. ¿Cuál es la pérdida de energía en metros de fluido?.
c.2 ¿Cuál es la potencia de la bomba?.
d. Compare con los resultados obtenidos en los ítems (a), (b) y (c).
Opine al respecto.
T(°C) D.R.  (m2/s)
30 0,86 7,00 x 10 - 6
80 0,93 1,20 x 10 - 6
120 0,96 2,52 x 10 - 6
SOLUCION
(a) Tubería horizontal
 = 0,0283 m3/s
D = 0,1524 m
L = 310 m
e = 0,046 mm
T = 30°C:
 = 860 kg/m3
 = 710- 6 m2/s.
La ecuación de energía entre (1) y (2):
p
z
V
g
p
z
V
g
h1
1
1
2
2
2
2
2
1 2
2 2 
      

p p
h1 2
1 2

 

 [1]
La caída de presión es igual a la pérdida por fricción.

4. 4
i)Cálculo de la pérdida de energía por fricción : h f
L
D
V
g1 2
2
2 
V
A
m s
m
m s




 , /
( , )
, /
4 0 0283
0 1524
155
3
2 2


VD
Re
74633
107
1524,055,1
Re 6
 
x
x
> 2000 → flujo turbulento
000301837,0
4,152
.046,0

mm
mm
D
e

La ecuación de Colebrook:









71,3Re
51,2
log25,0 
f
f









71,3
837301000,0
74633
51,2
log25,0
f
f
Se asume un valor de f (entre 0,010 y 0,025), igual a 0,02; se reemplaza
en el miembro derecho de la ecuación y se evalúa obteniéndose para f del
miembro izquierdo de la ecuación un valor de 0,0242. Como éste valor de
f calculado no es igual al valor de f asumido, se toma fasumido = 0,0242 y
se obtiene fcalculado = 0,0236 y así se continua hasta que los valores de f
asumido y fcalculado coincidan f = 0,0237.
f asum f as0,0200 0,0202 0,0237
f calc 0,0202 0,0237 0,0237
Luego: m
g
h 903,5
2
)55,1(
1524,0
310
0237,0
2
21  
ii) Presión indicada por el manómetro en la posición (2):
En [1]: m
mNx
pPax
903,5
/981086,0
1074,31
3
2
5


 p2 = 31,242x 105 Pa p2 = 31,24 bar
iii) La potencia que requiere la bomba: Potencia al eje



.p
P
watt
smPax
P 1769
80,0
/0283,010)24,3174,31( 35




5. 5
P = 1,769 kW
b) Tubería vertical: Como f = f (Re,  = e/D), y los valores de Re y
e/D se mantienen constantes, la pérdida por fricción será la misma:
h f
L
D
V
g1 2
2
2 
hf = 5,903 m
La ecuación de energía entre (1) y (2):
p p
Z h1 2
1 2

  

 
3174 10
0 86 9810
310 5 903
5
2
3
,
, /
,
 

 
Pa p
N m
m m
p2 = 5,088 x 105 Pa =  p2 = 5,09 bar
watt
smPax
P 27494
80,0
/0283,010)09,574,31( 35



P = 94,274 kW
c) Procediendo de la misma forma que el ítem (a):
V
A
m s
m
m s




 , /
( , )
, /
4 0 0283
0 1524
155
3
2 2

73893
1052,2
1524,055,1
Re 6
 
x
x
837301000,0
4,152
.046,0

mm
mm
D
e











71,3
837301000,0
93738
51,2
log2
5,0
f
f
fas = 0,0237 0,0194 0,0197 0,01966
fcalc = 0,0194 0,0197 0,01966 0,01967

6. 6
h
g
m1 2
2
0 0196
310
0 1524
155
2
4 882  ,
,
,
,
watt1457
0,80
s/m0,0283Pa4,8298100,86
P
3



 P = 1,457 KW
La potencia es aproximadamente el 82% de la potencia del caso (a).
Obviamente, este ahorro en la energía habrá de compararse con el costo de
elevar la temperatura a 120 °C.

7. 7
P3. Una bomba cuya curva de capacidad de carga se muestra en la figura, bombea
agua por un sistema. Determine el flujo volumétrico aproximado que hace circular la
bomba.

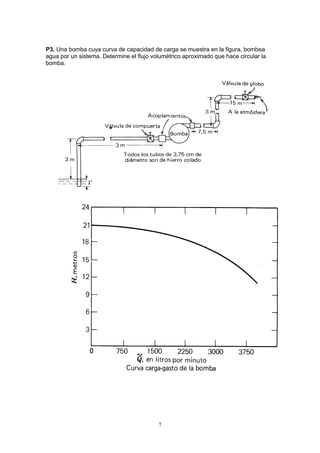
8. 8
25 mm
1,2 m
Z1
Z2
h =250 mm
1
2

DR Hg = 13,6
P2. Por la tubería mostrada fluye un aceite (S = 0,92 a razón de 6600 Litros / h, en el
sentido indicado en la figura.
a) ¿Cuál es el valor de la caída de presión? [ p1 - p2 ] en m de aceite?.
b) ¿Cuál es la pérdida debido a la fricción.
c) Hallar el factor de fricción f.
d) ¿Es flujo laminar ?. Evalúe el número de Reynolds Re.
e) Determine la viscosidad absoluta del aceite.
142 N

9. 9
RESUMEN
PERDIDAS SECUNDARIAS
8.4.1 EXPRESIONES ANALÍTICAS
8.4.2 COEFICIENTES EXPERIMENTALES 
8.4.3 LONGITUD EQUIVALENTE
( / )Lequiv L D D 
2 2
2 2
equiv efectL L LV V
h f f
D g D g
 
  
En un problema particular pueden presentarse el uso de estas tres formas de evaluar
la pérdida en elementos secundarios, con lo cual la pérdida secundaria estaría dado
por:


 
r
1
2
m
1
2n
1
hsi
g2
V
D
iLequ
f
g2
V
ihs
PERDIDA DE ENERGÍA EN UNA TUBERÍA:
PÉRDIDA PRIMARIA Y PÉRDIDAS SECUNDARIAS
22 2 2
1
1 1
( / )
( )
2 2 2 2
m
jn r
k
i
L D D
VL V V V
h f f
D g g D g g



    

 
∆ ℎ = [ 𝑓 [
𝐿
𝐷
+ Σ (
L
D
) ] + Σ 𝜆 + Σ K ]
𝑉𝑖
2
2 𝑔
2
2
V
hs
g

2 2
1 2
2
V V
hs
g



10. 10
D: en pulgadas

11. 11
D: en pulgadas

12. 12

13. 13

14. 14

15. 15

16. 16
8.9 Se requiere impulsar 5 000 GPM (USA) de agua fría ( = 1,000176429
m 2 /s ) de un reservorio A, abierto a la atmósfera, hacia un reservorio B que se
encuentra a una presión manométrica p2 = 250 kPa, siendo la tubería de acero
estirada NR 40 ( e = 0,1 mm ) para la línea de succión y la línea de descarga.
La línea de succión es de 4 m de longitud, 20 pulgadas de diámetro
nominal y tiene los siguientes elementos roscados: Cedazo de
aspiración, un codo radio largo, dos uniones universales y una válvula de
compuerta.
La línea de descarga es de 14 pulgadas de diámetro nominal, 165 m de
longitud, y tiene los siguientes accesorios: Una válvula de globo, una
válvula de retención, tres uniones universales, dieciséis uniones simples
y tres codos radio largo.
Tomando como referencia el eje de la bomba, se tiene que la superficie
libre líquida del reservorio A se encuentra a -2 m y la superficie libre
del reservorio B se encuentra a 15 m; ambas distancias permanecen
constantes.
a. Calcule la pérdida de carga en el sistema.
b. Seleccione una bomba comercial.
c. Una vez instalada la bomba, se tiene que el manómetro en la
entrada a la bomba indica una presión de vacío de 25,649 kPa,
¿Cuál será la lectura en el manómetro colocado en la salida de la
bomba?.
d. Elabore una hoja de cálculo para la solución de este problema.

17. 17
SOLUCION
a) La pérdida de carga en el sistema: h
Está dada por la pérdida de carga en la tubería de succión y la pérdida de carga en la
tubería de descarga:
adescsucción hhh arg [1]
(I) Tubería de succión.
Existe pérdida de carga en la tubería, accesorios, válvulas y elementos de
control. La pérdida en los elementos secundarios se pueden expresar en
términos del coeficiente lambda, longitud equivalente o expresiones analíticas.
)2(
2 .
..
2
comp
válvulauuncodoentrada
s
succión
D
L
f
g
Vs
h   [2]
De la tabla: 12b, 12c cmDNRD iss 79,4740,02  
Para evaluar la velocidad del fluido, previamente habrá que calcular el flujo
volumétrico.
El caudal o flujo volumétrico:
-5
106,308xGPM5000 
/sm0,3154 3

Velocidad media:
2
0,4779/0,3154x4 sV
/sm758,12 V
El coeficiente de fricción f se determina considerando el valor del número de
Reynold (Re) y la rugosidad relativa (.
 = 1,000176429 m 2 / s
Re = 1,758 m / s x 0,4779 m / 1,000176429 m 2 / s = 840 000
 = 0,01 mm / 477,9 mm = 0,00021

18. 18
El factor de fricción f
Re =  V D /  = 840000
 e / D = 0,00021
La ecuación de Colebrook :
f asumido = 0,01 0,01514 0,01493
f calculado = 0,01514 0,01493 0,01494
ú
ú
û
ù
ê
ê
ë
é


71,3Re
51,2
log2
5,0 
asumidocalculado f
f
ú
ú
û
ù
ê
ê
ë
é


71,3
00021,0
000840
51,2
log2
5,0
asumido
calculado f
f
.0149,0sf
Las pérdidas secundarias:
El uso de los coeficientes lambda requiere el uso de la variación en los
valores dados.
De la tabla 4a, 4b, y 4c; se tiene:  %
 Cedazo de aspiración: 5040,0   0,060
 Codo RL: DN = 20´´ 2510,0   0,125
 Válvula de compuerta : DN = 20´´ 2530,0   0,375
 Uniones: DN = 20´´ 5003,0   0,045
Reemplazando valores en [2]:
)375,0045,02125,06,0
4779,0
4
0149,0(
2
758,1 2

g
hsucc
.2071,0 aguademhsucc   [3]
(II) Tubería de descarga o impulsión: De manera similar

19. 19
)3163(
2
....
2
arg
RL
codounivuuun
válvula
reten
válvula
globo
d
adesc
D
L
f
g
Vd
h  
[4]
Reemplazando valores en [2]:
cmDD idd 33,33"14  
s/m615,3dV
0003,03,333/1,0 
6
10x1,2Re 
0155,0df
De la tabla 4a, 4b, y 4c; se tiene:  %
 Codo RL: DN = 14´´ 2512,0   0,150
 Válvula de retención : DN = 14´´ 3000,2   2.600
 Válvula de globo : DN = 14´´ 2550,5   6,875
 Uniones: DN = 14´´ 5003,0   0,045
Reemplazando valores en la ecuación [4]:
)150,03045,016045,036,2875,6
3333,0
165
0155,0(
2
615,3 2
arg 
g
h adesc
.2907,12arg aguademh adesc   [5]
Reemplazando [3] y [5] en [1]:
maguademmmh 5,12.4978,122907,122071,0  
b) Selección de la bomba:
Se requiere especificar la carga total H y el flujo volumétrico 
Ecuación de energía entre 1 y 2:
21
2
1
2
2
12
12
2




 h
g
VV
zz
pp
H

mmmH 5,1217
9810
000250
 = 25,484 17 12,5 54,984m m m m  

20. 20
H = 55 m <> 180 pies
GPM0005
Los fabricantes ofrecen lo que ellos denominan familias de bombas, y de allí
una en particular que cumpla con abastecer del caudal y altura dados y, la
bomba funcionando con una eficiencia aceptable para el servicio que presta el
equipo de bombeo.
De la figura A, la bomba: A-1015L cubre las necesidades,.

21. 21
De la figura B, se tiene que el diámetro del impulsor es de 14,6 pulgadas; la
eficiencia %89 ;y se requiere 260 HP ( 194 kW ) para mover la bomba.
c) Cálculo de la lectura de la presión colocado en la descarga de la bomba:
La ecuación de energía entre la entrada y salida de la bomba:
gVzpH 2// 2
 
 
g
VV
ZsZdm
p
m
p
H sdsd
2
)()25,0()6,0(
22



Reemplazando valores:
  mmm
p
H d
683,545085,0025,0614576,2)6,0( 

mPd 2099,51/  .369,502 kPaPd  

22. 22
También puede determinarse dP , planteando la ecuación de energía entre la
descarga de la bomba (d) y la superficie libre del reservorio B, punto (2).
 gVz
p
dd
d
2/2

2
2
2
2
2
 d
d
h
g
V
z
p








g
Pd
2
615,3
06,0
2

991,11015
9810
000250
 m m475,52
m
Pd
209,51

de agua fría.
2
/9810209,51 smmPd 
.360,502 KPaPd  
EJEMPLO: Se va a construir un sistema de bombeo similar, para lo cual la
tubería será nueva (e = 0,0456 mm), y la bomba a utilizar será del mismo tipo.
a. Determine la pérdida de carga en el sistema, cuando se impulse
5000GPM.
b. Manteniendo las válvulas totalmente abiertas, el nuevo caudal impulsado
¿será mayor o menor a 5000 GPM?. ¿porqué?.
Sugerencia: Haga uso de la hoja de Excel elaborada para el problema anterior.

23. 23
EJEMPLO : La figura muestra un sistema de cañerías que proporciona 4 m 3 /
min de agua a 21°C para un proceso. La tubería es de acero soldado sin
costura, de diámetro interior 25,4 cm y rugosidad absoluta igual a 0,046 mm.
Determine:
a. La pérdida de carga sólo en la tubería. ∆ h f
b. La pérdida de carga en los accesorios.  h i .
c. La pérdida de carga en el sistema. ∆ h s .
d. La altura de la bomba. H B.
e. La potencia para accionar la bomba, si ésta tiene una eficiencia
del 87%.
f. Una expresión para la altura de la bomba : H B = A + B  n

24. 24
P La figura muestra una bomba que debe elevar agua (a 20C) de un pozo
a un tanque hidroneumático. Se conocen los siguientes datos característicos
de la bomba:
Item
Flujo volumétrico
Litros / minuto
Altura (HB)
metros
Eficiencia
%
1 0 100 0
2 300 100 30
3 600 95 60
4 900 89 68
5 1200 78 65
a. Determinar el flujo volumétrico que la bomba impulsa, la eficiencia de la
bomba y la potencia que el motor debe de entregar a la bomba.
b. Estimar la presión manométrica en la succión de la bomba.
c. Obtener una expresión analítica para la curva del sistema de la forma :
HB = A + B n
d. Determinar si las válvulas de pie y de retención funcionan en su posición
abierta, suponiendo que éstas válvulas requieren una caída mínima de
1034 Pa si están abiertas
p = 29 430 Pa

25. 25
PUNTO DE OPERACION DE LA BOMBA
HB BOMBA
HB SISTEMA
Eficiencia
Punto de
operación
680 L / min
H m
93,8 m

26. 26
SISTEMA DE TUBERIAS EN SERIE
La literatura reporta la siguiente información:
Para flujo turbulento desarrollado en una tubería de longitud L, se puede
identificar tres categorías de problemas:
CATEGORIA DATOS INCÓGNITA
1
 , D, e,  hf
2 D , e, , hf, 
3
 , e, , hf,
D
Los problemas de la categoría 1 son directos y no requieren un procedimiento
de iteración cuando se usa el diagrama de Moody o la ecuación de colebrook.
Los problemas de las categorías 1 y 2 requieren un proceso iterativo de ensayo
y error al utilizar el diagrama de Moody o la ecuación de Colebrook.
Una alternativa al uso del Diagrama de Moody o la ecuación de Colebrook,que
evita los procedimientos de prueba y error, es utilizar fórmulas deducidas
empíricamente. Una de tales fórmulas son las que presentaron Swamee y Jain
(1976) para flujos en tuberías:
2
9,0
5
2
62,4
7,3
07,1









ú
ú
û
ù
ê
ê
ë
é











 D
D
e
Ln
Dg
L
hf

[1]
Válido para: 10 – 6 < e / D < 10 – 2 3000 < Re < 3x10 8
ú
ú
ú
û
ù
ê
ê
ê
ë
é


















5,0
3
2
5,05
17,3
7,3
965,0
f
f
hDg
L
D
e
Ln
L
hDg 
Re> 2000 [2]
0,044,75 5,2
2
1,25 9,4
0,66
f f
L L
D e
g h g h

                  
[3]
Válido para: 10 – 6
< e/D < 10 – 2
5000 < Re < 3x10 8

27. 27
Estas ecuaciones dan un valor aproximado para la incógnita de cada una de las
categorías de problemas anteriores; y son válidas tanto para el sistema SI como para
unidades inglesas.
La ecuación [2] es tan exacta como el Diagrama de Moody, y las ecuaciones [1] y [3]
producen valores que difieren en menos del 2% respecto a los obtenidos con el
Diagrama de Moody.
P1. Un flujo volumétrico de 0,003 m3
/s de agua se transporta por una tubería horizontal
de hierro forjado de 4 cm de diámetro interior Calcule la pérdida de carga
debido a la fricción en un tramo de 500 m de longitud y la potencia necesaria
para impulsar dicho caudal, si la eficiencia de la bomba es del 85%.
a. Utilizando la ecuación de Colebrook
b. Utilizando la ecuación semiempírica de Swamee y Jain
SOLUCIÓN
La pérdida de carga hf:
g
V
D
L
fh f
2
2
 [a].
Hay que calcular f y V.
La velocidad media: 2
4
DA
V






 sm
m
m
V /387,2
04,0
003,04
22
3




El número de Reynolds:
D
DVDV

 

4
Re
48095
10
04,0387,2
Re 6


 
DV
Régimen turbulento.
La rugosidad relativa:
D
e
  00115,0
40
046,0

mm
mm

La ecuación de Colebrook:
ú
ú
û
ù
ê
ê
ë
é


71,3Re
51,2
log2
5,0 
f
f
ú
ú
û
ù
ê
ê
ë
é


71,3
15001,0
020,048095
51,2
log2
5,0
f
fasm = 0,020 0,0229 0,0227 0,0228 0,02275
fcalc 0,0229 0,0227 0,02275 0,02275 0,02275

28. 28
Remplazando valores en la ecuación [a]: m
g
h f 58,82
2
387,2
04,0
500
02275,0
2

La caída de presión en la tubería horizontal:
Pam
m
N
hp f 15281058,829810 3
 
La potencia requerida por la bomba:



p
P
kWWatts
smPa
P 32859
85,0
/003,0152810 3



Utilizando la ecuación [1]:
2
9,0
5
2
62,4
7,3
07,1









ú
ú
û
ù
ê
ê
ë
é











 D
D
e
Ln
Dg
L
hf

mLn
g
hf 969,82
003,0
04,010
62,4
407,3
046,0
04,0
500003,0
07,1
2
9,0
5
2 6









ú
ú
û
ù
ê
ê
ë
é







 






P2. En un tramo de 300 m de una tubería horizontal de hierro forjado de 10 cm de
diámetro interior, se mide una caida de presión de 700 KPa cuando transporta
petróleo (DR = 0,9;  = 10 - 5
m2
/s). Determine el flujo volumétrico en GPM.
a. Utilizando la ecuación de Colebrook.
b. Utilizando la ecuación semiempírica de Swamee y Jain.
SOLUCIÓN
La rugosidad relativa:
D
e
  00046,0
100
046,0

mm
mm

Considerando flujo completamente turbulento:
ú
û
ù
ê
ë
é


71,3
log2
5,0 f  01638,0
71,3
00046,0
log2
5,0
ú
û
ù
ê
ë
é


ff
La pérdida de carga hf:

p
g
V
D
L
fh f


2
2
smV
g
V
h f /931,5
9,09810
000700
210,0
300
01638,0
2




29. 29
El número de Reynolds: 31059
10
104,0931,5
Re 5


 
DV
Así: La ecuación de Colebrook:
ú
ú
û
ù
ê
ê
ë
é


71,3Re
51,2
log2
5,0 
f
f
ú
ú
û
ù
ê
ê
ë
é


71,3
00046,0
017,031059
51,2
log2
5,0
f
fasm = 0,017 0,0223 0,0218
fcalc 0,0223 0,0218 0,0218
Luego, la pérdida de carga:
smV
g
V
h f /877,4
9,09810
000700
210,0
300
0218,0
2



77048
10
10,0877,4
Re 5


 
DV
ú
ú
û
ù
ê
ê
ë
é


71,3
00046,0
0218,077048
51,2
log2
5,0
f
fasm = 0,0218 0,0226 0,0225
fcalc 0,0226 0,0225 0,0225
smV
g
V
h f /800,4
9,09810
000700
210,0
300
0225,0
2



00048
10
10,0800,4
Re 5


 
DV
ú
ú
û
ù
ê
ê
ë
é


71,3
00046,0
0225,000048
51,2
log2
5,0
f

30. 30
fasm = 0,0225 0,0226
fcalc 0,0226 0,02259
smV
g
V
h f /7899,4
9,09810
000700
210,0
300
0226,0
2



90047
10
10,079,4
Re 5


 
DV
ú
ú
û
ù
ê
ê
ë
é


71,3
00046,0
0226,090047
51,2
log2
5,0
f
fasm = 0,0226
fcalc 0,0226

  smmsmAV /03762,0
4
10,0
/79,4 32
2


Como 1 GPM <> 6,3083 x 10 – 5
m3
/s   =596,357 GPM
Utilizando la ecuación [2]:
ú
ú
ú
û
ù
ê
ê
ê
ë
é


















5,0
3
2
5,05
17,3
7,3
965,0
f
f
hDg
L
D
e
Ln
L
hDg  Re> 2000
 
ú
ú
ú
û
ù
ê
ê
ê
ë
é




















 


5,0
3
25,05
28,7910,0
3001017,3
1007,3
046,0
300
28,7910,0
965,0
5
gmm
mm
Ln
g
sm /610037,0 3

P3. Determine el diámetro de tubo estirado que debe escogerse para transportar 0,002
m3
/s de agua a 20 °C una distancia de 400 m sin que la pérdida de carga
exceda 30 m.
a. Utilizando la ecuación de Colebrook.
b. Utilizando la ecuación semiempírica de Swamee y Jain.

31. 31
SOLUCION
La velocidad media: 2
4
DA
V






sm
DmD
m
V /
00255,0002,04
222
3




La pérdida de carga hf:
g
V
D
L
fh f
2
2

 
g
D
D
m
fm
2
/00255,0400
30
22

D5
= 4,42 x 10 – 6
f [1]
DD
DDV 2550
10
00255,0
Re
26


 
[2]
La rugosidad relativa:
D
e
 
mD
m0015000,0
 [3]
La ecuación de Colebrook:
ú
ú
û
ù
ê
ê
ë
é


71,3Re
51,2
log2
5,0 
f
f [4]
fasm = 0,03 0,02
De [1]: D = 0,0421 m 0,0388
De [2]: Re = 6,06 E4 6,57 E4
De [3]:  = 0,000036 0,000039
De [4]: fcalc = 0,02 0,02
Reemplazando en [1]: D = 0,0388 m  D = 4 cm

32. 32
Utilizando la ecuación semi-empírica [3], de Swamee y Jain:
04,02,5
4,9
75,4
2
25,1
66,0


























 

ff hg
L
D
hg
L
eD 

[3]
Válido para: 10 – 6
< e/D < 10 – 2
5000 < Re < 3x10 8
     
04,0
2,5
4,9
75,42
25,1
3081,9
400
002,010
3081,9
002,0400
0015000,066,0
6





























D
D = 0,039 m D = 4 cm
P4. Calcular el flujo de agua que se descarga del reservorio superior de la tubería lisa
(
25,0
Re346,0f ) que se muestra en la figura:
Solución:
Ecuación de energía entre el punto [1] y el punto [B]:
g
V
D
L
f
g
Vpp
zz
h
g
V
z
p
g
V
z
p
BBB
B
B
B
B
22
22
22
1
21
1
22
1
1
1



 


2 m
8 m
2 m
D = 100 mm

33. 33
)
10,0
8
1(
2
210
2
f
g
V
mm B

Tubería lisa
25,0
6
10
10,0
316,0





 


BV
f
A
vg
V
m
B
B









 25,0
2
4216,1
1
2
8
Vasum 9 m/s 9,5 9,3 9,31
A 7,516 8,32 7,9968 8,013
Luego:
 
./307304,0
/07304,010,0
4
/3,9./3,9 32
sm
smsmsmVB



 
P5. Calcular la potencia necesaria para bombear un fluido (  = 0,04 Pa-s; DR = 1,83 )
a 45 litros / s desde un tanque de suministro y a través de una tubería recubierta
de vidrio de 150 mm de diámetro y 18 m de longitud, hasta un tanque de
almacenamiento. El nivel del líquido en el tanque de almacenamiento se
encuentra a 6 m arriba que el nivel en el tanque de suministro. Sobre las
superficies libres líquidas puede asumirse presión atmosférica. Considere las
pérdidas en la entrada  = 0,5 y en la salida de la tubería  = 1,0.
Solución:
La ecuación de energía: 21
2
2




 hz
g
V
g
p
hweje







 salidaentradaeje
D
L
f
g
V
mhw 
2
600
2
 
./546,2
15,0
/045,0
22
3
sm
m
sm
A
V 






Tipo de Régimen de flujo:  /Re VD
17475
04,0
15,0546,21830
Re 

 Turbulento
Luego el factor de fricción, puede obtenerse de la ecuación de Colebrook:

34. 34
02675,0
71,3Re
51,2
log25,0










f
f
f

Donde: 0
D
o
D
e

asumf 0,006 0,033 0,0259 0,02687 0,02673 0,02675
calculadof 0,033 0,0259 0,02687 0,02673 0,02675 0,02675
mejehw
mmm
mmm
m
g
mhweje
5561,7
49557,006053,16
33038,016519,006053,16
0,15,0
15,0
18
02675,0
2
546,2
6
2










La potencia:
.
5561,7045,083,19810
410,6
3
3
KwPot
m
s
m
m
N
hwPot
hwAVghwgmPot
eje
ejeeje








Obsérvese que la pérdida secundaria representa el 31,847% de la pérdida de
la carga.