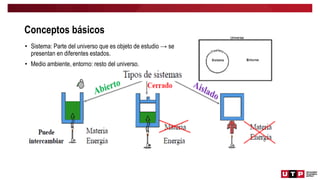
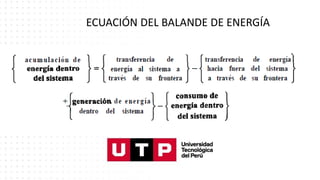
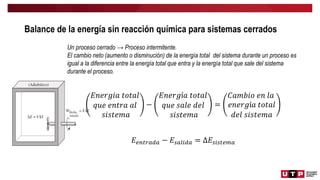
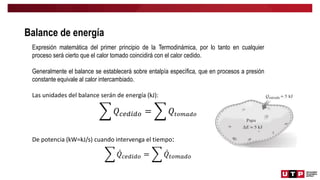
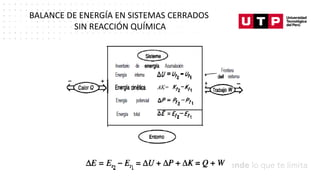
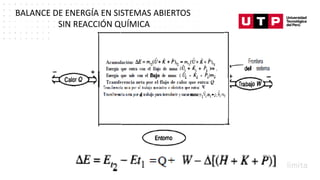
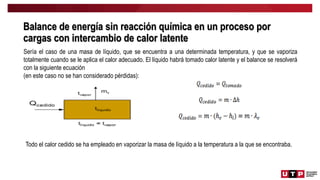
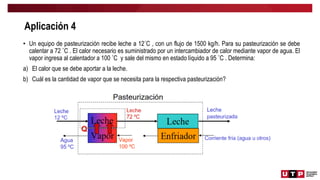
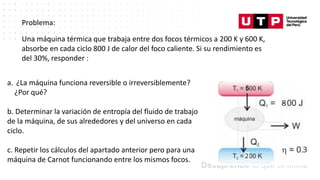
Este documento trata sobre el balance de energía y procesos auxiliares. Explica los conceptos básicos del balance de energía, incluidas las ecuaciones para sistemas cerrados y abiertos sin reacción química. También cubre el cálculo del balance de energía para procesos con intercambio de calor sensible y latente, tanto para procesos por cargas como continuos. Por último, incluye ejemplos numéricos de aplicación del balance de energía.